Galois field arithmetic for encoding information by Reed-Solomon codes

Reed-Solomon codes refer to non-binary, block, noise-resistant codes and can be used in the field of information storage to avoid the loss of damaged information.


On Habré there is a post dedicated to the coding of information with Reed-Solomon codes, but for example the author uses a simple Galois field. This article describes the work with extended Galois fields, in particular GF (2 ^ m), which are rationally used for digital information. With my similar implementation of encoding, decoding, error correction can be found here .

When working with Reed-Solomon codes, the percentage of redundant characters is 2 times the recoverable amount of data. Let me explain with an example: if we have a sequence of 10 characters and want to be able to recover errors in 3 of them (30% of the initial information), then we need to store 10 + 3 * 2 = 16 characters. Call each variable: n = 10, the number of information characters; f = 3, the number of characters to be restored; g = 16, the length of the encoded sequence. Thus, the formula can be written as: g = n + f * 2.
')

Paul Galois

To work with information when encoding and decoding data, all arithmetic operations are performed in the Galois fields. The so-called polynomial arithmetic or Galois field arithmetic is used. Thus, the result of any operation is also an element of this field. A specific Galois field consists of a fixed range of numbers. A characteristic of the field is some prime p. Field order, i.e. the number of its elements is some natural degree of the characteristic pm, where m∈N. When m = 1, the field is called simple. In the cases when m> 1, a polynomial of degree m is needed to form a field, such a field is called extended. GF (p ^ m) - Galois field designation.

To work with digital data, it is natural to use p = 2 as a field characteristic. When m = 1, the bit sequence will be an element of the code sequence, while m = 8 will be 8 bits, that is, a byte. Actually Reed-Solomon codes working with bytes and are the most common.

Before proceeding to the operations of encoding and decoding, we shall deal with the arithmetic of Galois fields using the example of GF (2 ^ 3). This field consists of numbers from 0 to 7.

Addition operation

The simplest is the addition operation, which is a simple bitwise addition modulo 2 (XOR).

Example: 5 + 3 = 110 = 6

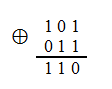
Multiplication operation

Unfortunately, the multiplication operation is much more difficult; in order to perform it, it is necessary to convert numbers into a polynomial form.

Example: 5 = 101 = 1 ∙ x ^ 2 + 0 ∙ x ^ 1 + 1 ∙ x ^ 0 = x ^ 2 + 1

As you can see a number in polynomial form is a polynomial whose coefficients are the values ​​of bits in the binary representation of a number.

Multiply two numbers in polynomial form:
5 ∙ 7 = (x ^ 2 + 1) (x ^ 2 + x + 1) = x ^ 4 + x ^ 3 + x ^ 2 + x ^ 2 + x + 1 = x ^ 4 + x ^ 3 + x + 1 = 11011 = 27

So, first of all, it should be noted that modulo 2 addition is carried out even in a polynomial form, therefore x ^ 2 + x ^ 2 = 0. Secondly, the result of multiplication 27 is not included in the used field GF (2 ^ 3) (it also consists of numbers from 0 to 7, as mentioned above). To deal with this problem, you must use the generator polynomial. The generating polynomial is irreducible, that is, simple (by analogy with prime numbers, it is divisible by 1 and by itself). In the arithmetic of Galois fields, an irreducible polynomial is an analog of prime numbers. For example, we use the generator polynomial f (x) = x ^ 3 + x + 1.

It is also assumed that x satisfies the equation f (x) = x ^ 3 + x + 1 = 0

Let's go back to the multiplication example:

The same result can be obtained as the remainder of dividing a polynomial obtained by multiplying by the generating polynomial:


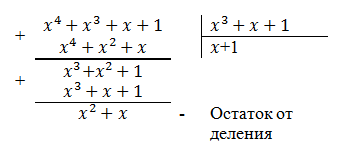
Let's make the multiplication table:

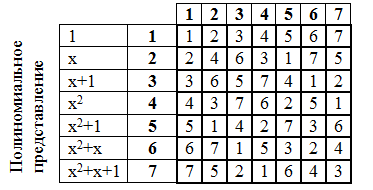
Division operation

The division operation in a polynomial form is understandable, but it is rather difficult. Therefore, it is much better to implement it according to the multiplication table.

Example: 6 ÷ 5 = 7

Of great importance is the table of degrees of elements of the Galois field. Exponentiation is also carried out in a polynomial form, similar to multiplication.

Example: 5 ^ 2 = 〖(x ^ 2 + 1)〗 ^ 2 = x ^ 4 + x ^ 2 + x ^ 2 + 1 = x ^ 4 + x ^ 2 + x + x ^ 2 + x + 1 = x ∙ (x ^ 3 + x + 1) = x ^ 2 + x + 1 = 111 = 7

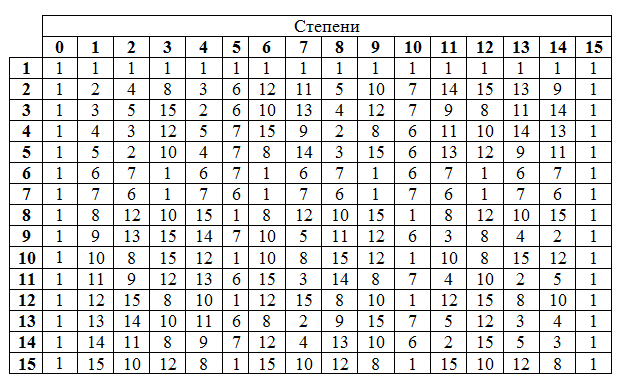
Thus, we make a table of degrees:


The degree table is cyclical: the seventh degree corresponds to zero, which means the eighth corresponds to the first, and so on. If you wish, you can check it out.

In Galois fields, there is the concept of a primitive member - a field element whose degrees contain all non-zero field elements. After reviewing the table of degrees, it is clear that all the elements correspond to this condition (well, except for 1 naturally). However, this is not always the case; for example, I will give a degree table for GF (16).



For the fields that we consider, that is, with characteristic 2, always choose 2. as the primitive member. Given its property, any element of the field can be expressed in terms of the degree of the primitive member.
Example: 5 = 26, 7 = 25

Using this property, and taking into account the cyclical nature of the table of degrees, we will try to multiply the numbers again:
5 ∙ 7 = 2 ^ 6 ∙ 2 ^ 5 = 2 ^ (6 + 5) = 2 ^ 11 = 2 ^ (11 mod 7) = 2 ^ 4 = 6
The result coincided with what we calculated earlier.

And now let's do the division:
6 ÷ 5 = 2 ^ 4 ÷ 2 ^ 6 = 2 ^ (4-6) = 2 ^ (- 2) = 2 ^ ((- 2) mod 7) = 2 ^ 5 = 7
The result obtained is also true.

Well, for completeness, let's look at the exponentiation:
5 ^ 2 = (〖2 ^ 6)〗 ^ 2 = 2 ^ (6 ∙ 2) = 2 ^ 12 = 2 ^ (12 mod 7) = 2 ^ 5 = 7
Again, the same result was unexpected.

This approach to multiplication and division is much simpler than real operations with the use of polynomials, and for them there is no need to store a large multiplication table, but only a string of powers of a primitive field member is sufficient.