On solving an incomplete cubic equation

Intro

I publish this topic as an educational. As a matter of fact, there is no significant novelty in the material, the topic is jaded. I think that the approach to solving the problem will be interesting.

I remember that in the first year in the classroom on mathematical analysis, one integral came to mind. The teacher called to the blackboard, but the bell rang. On the way home, a “skeleton” of solving a cubic equation took shape on the bus. The general scheme, of course, is not the most rational. There is a more effective - Vieht trigonometric formula . There, the root is immediately written out by the form of the equation, and, in general, the volume of calculations is still better to use the Newton's numerical method, since the power series for inverse trigonometric functions converge slowly (they compute such functions in some libraries). That's what happened.

1. Source integral and cubic equation

Need to find an indefinite integral
')


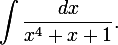
Using the method of indefinite coefficients, we represent the denominator of the integrand as



whence we obtain a nonlinear system of algebraic equations for unknown coefficients, the solution of which requires finding a positive root of an incomplete cubic equation



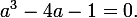
Exploring the function in the left side of the equation for monotony, it can be found that it has a maximum



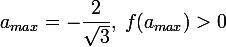
and minimum



Wherein



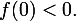
Then from the continuity of the function it follows that the original equation has three real roots, with two negative and one positive, belonging to the segment , .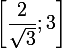
Let's find him.

2. The search for a positive solution

Note that our equation has no rational roots.
Let's start with the following identity, the validity of which, probably, was proved by many at school:



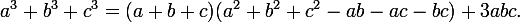
Convert it to mind



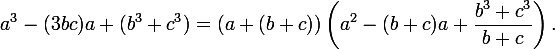
Then the solution of the cubic equation is reduced to the solution of the system



where 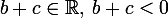(according to the condition of positivity of the root).
From this system go to the system



Essentially, Wyeth's theorem for a quadratic equation is written in (1)



or



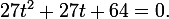
The discriminant here is negative, it would seem that the solution can be completed, but we do not need reality 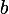and and the validity of their amount. This will help complex numbers.

The trigonometric form for writing the roots of a quadratic equation has the form

,
Where - imaginary unit.

Then



A question may arise: in system (1), the first equation was obtained by building both sides into a cube, will this cause the appearance of additional complex roots? No, because if to express 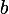through in the original system, we get the quadratic equation already considered. When expressing through 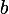we have the same thing. This proves the validity of the last aggregate.
Extract the cube root from 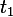and 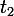by the rule of extracting roots from complex numbers. Will get



Where


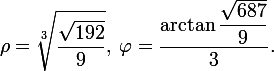
Choose such a pair 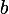and so that their sum in the imaginary part of the complex number is 0 , and the real part would be negative. In this case, we will use the reduction formulas (if you need to find the remaining roots of the equation, then it is better to use formulas for converting the sum of trigonometric functions into a product), and also take into account that the angle 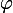belongs to the first quarter. Then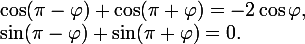



Where did the desired root


If you use the trigonometric formula Vieta, then the resulting root will be written in a more simple form


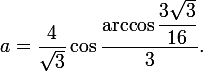
The question arises: why did I not use the Cardano formula ? After all, in schools we were told that they use it to solve cubic equations. In its form, it is similar to what I have done now - in the end, you will have to extract the cube root from a complex number. By the way, it was in solving equations of the third degree that complex numbers first got their use.

I note that to clarify the composition of the roots of a cubic equation , the concept of a discriminant is used (as in the case of a quadratic equation). In general, the concept of a discriminant in algebra is introduced for polynomials of arbitrary degree.

2. An example of a physical problem with a cubic equation

In the journal "Kvant" I once came across an interesting problem in physics with the exit to the solution of the cubic equation. The essence is as follows. Need to determine what the maximum speed can develop a car mass (together with a man) with a known highest power engine?
At the highest vehicle speed, its acceleration is zero, since the derivative of the function vanishes at the extremum point. Although it is zero when driving at a constant speed. Then you can say this: what is the maximum constant speed a car can develop?
At high speeds, it is no longer possible to neglect air resistance, and the drag force is not expressed according to the Stokes law , but according to a quadratic law, since the speed of movement is quite large. Then the thrust force of the engine is balanced by the force of air resistance and the forces of rolling friction and slip that occur between the tire wheel of the car and the roadway:



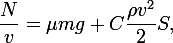
Where 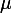- total coefficient of friction, - acceleration of gravity, - coefficient of aerodynamic drag , 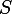- the area of ​​the frontal section of the car, whence we get an incomplete cubic equation.

3. Questions and Answers

When reading the topic, the reader may have questions. For example, such:

1. Why did the author not consider the full cubic equation? Answer: a complete cubic equation reduces to an incomplete replacement.



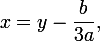
Where - new variable 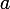- coefficient at 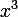, 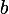- coefficient at .

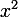2. At the beginning of the topic a fourth degree polynomial was considered. Are there any methods to solve such equations analytically? The answer is yes, there is a Ferrari method .

3. By the Abel-Ruffini theorem, an equation higher than fourth degree is not solvable in radicals. And here we have the root of a cubic equation containing trigonometric functions, which, most likely, cannot be expressed through radicals, how so? Answer: in the formulation of the theorem we mean the general record of the root, i.e. roots can also be extracted from complex numbers by substituting an equation into the coefficient formulas.

4. After Evarist Galois, were there any attempts to derive the root formulas of an equation of arbitrary degree? Answer: Not so long ago, I caught the eye of the Russian translation of the book of lectures on theta functions by American mathematician David Mumford (Mir, 1988). There, as an addendum, Hiroshi Umemur’s work “Solving Algebraic Equations Using Theta Constants” is presented, where the root extraction function is replaced by another function — the Siegel modular function expressed through theta constants. This paper also highlights the history of research on this issue after Galois.

5. As I understand it, such formulas are not applicable for use in practical problems of solving equations of arbitrary degree. Are there any modern works describing the algorithms for obtaining approximate roots? Answer: I advise G.P. Kutischeva, “Solving Algebraic Equations of Arbitrary Degree: Theory, Methods, Algorithms” (URSS, 2010).

6. Are there any modern modifications of Newton's numerical method, which is currently the main one for obtaining approximate solutions of equations and systems of equations? Answer: You can see the article by Janak Raj Sharma, Rangan Kumar Guha and Rajni Sharma "An efficient fourth order method" .

7. Are there any particular cases of equations of high degree for which we managed to obtain analytical formulas of the roots? Answer: Bring's root for finding a real solution of a fifth degree equation and the Lawrence Glasser formula for incomplete equations of arbitrary degree.

In conclusion for beginners I recommend the book of S.L. Tabachnikova and D.B. Fuchs's “Mathematical Divertissement” (ICNMO, 2010).