The perfect breaking of the pyramid of balls in billiards
Professor Jim Belk has shown that Mathematica is useful not only in science, but also in everyday life. At the request of a billiards fan, the professor calculated the trajectory of the balls when splitting with a cue ball perfectly in the center of the pyramid.
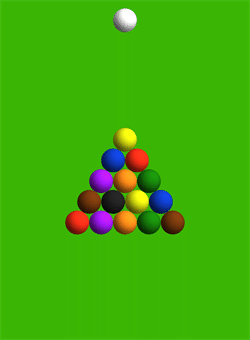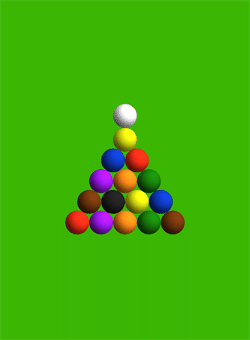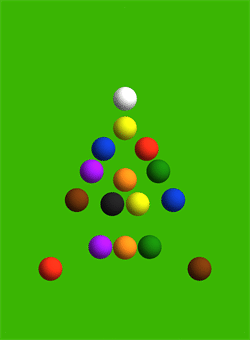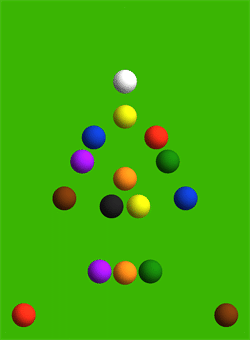
The trajectories are set using numerical solution of differential equations.
In this case, some assumptions are made:
')
* all balls are considered perfectly elastic and almost ideally rigid;
* each ball has a mass of 1 unit and a radius of 1 unit;
* The cue ball moves at a speed of 10 units per second;
* the interaction between two balls is described by the formula
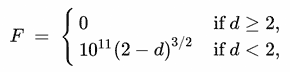
where d is the distance between the centers of the balls,
The formula is based on the laws of mechanics of contact interaction .
According to this model, all interactions between the balls fall within 0.2 milliseconds and not a single ball shrinks upon impact more than 0.025% of its radius.
The illustration shows the interaction forces between each pair of colliding balls. Interestingly, in the process of colliding the entire pyramid, the balls practically do not move.

The professor calculated the direction and speed of movement of each of the 15 balls of the pyramid, as well as the cue ball. In accordance with the calculation, the angular balls 11 and 15 should fly off the hardest: their initial speed is 5.6 units per second, that is 56% of the cue ball speed. The slowest moving ball is No. 5 in the very center of the pyramid: the speed is 0.12 units per second.

The speed and direction of each ball are shown in the table.

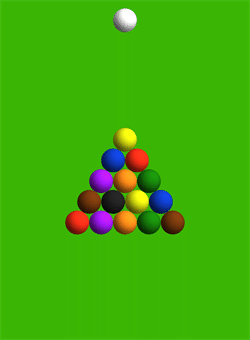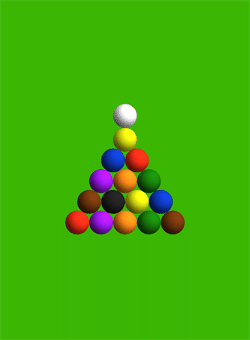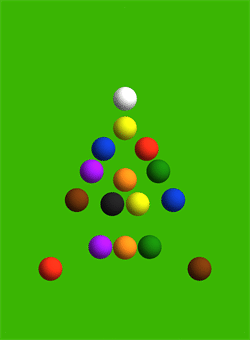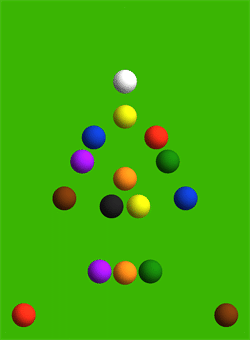
The trajectories are set using numerical solution of differential equations.
In this case, some assumptions are made:
')
* all balls are considered perfectly elastic and almost ideally rigid;
* each ball has a mass of 1 unit and a radius of 1 unit;
* The cue ball moves at a speed of 10 units per second;
* the interaction between two balls is described by the formula
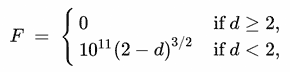
where d is the distance between the centers of the balls,
The formula is based on the laws of mechanics of contact interaction .
According to this model, all interactions between the balls fall within 0.2 milliseconds and not a single ball shrinks upon impact more than 0.025% of its radius.
The illustration shows the interaction forces between each pair of colliding balls. Interestingly, in the process of colliding the entire pyramid, the balls practically do not move.

The professor calculated the direction and speed of movement of each of the 15 balls of the pyramid, as well as the cue ball. In accordance with the calculation, the angular balls 11 and 15 should fly off the hardest: their initial speed is 5.6 units per second, that is 56% of the cue ball speed. The slowest moving ball is No. 5 in the very center of the pyramid: the speed is 0.12 units per second.

The speed and direction of each ball are shown in the table.

Source: https://habr.com/ru/post/211324/
All Articles