Counting Hamming distances on a large dataset
This article will discuss the HEngine algorithm and the implementation of the solution to the problem of calculating the Hamming distance on large data volumes.
Hamming distance is the number of different positions for rows with the same length. For example, HD ( 1 0 0 , 0 0 1 ) = 2.
For the first time, the problem of calculating the Hamming distance was posed by Minsky and Papert in 1969 [1], where the task was to search for all the rows from the database that are within the specified Hamming distance to the requested one.
Such a task is unusually simple, but the search for its effective solution still remains on the agenda.
')
Hamming distance is already quite widely used for various tasks, such as finding close duplicates, pattern recognition, document classification, error correction, virus detection, etc.
For example, Manku and associates proposed a solution to the problem of clustering duplicates when indexing web documents based on Hamming distance [2].
Also, Miller and friends suggested the concept of searching songs for a given audio fragment [3], [4].
Similar solutions were used for the task of image search and recognition of the retina [5], [6], etc.
There is a database of binary strings T , of size n , where the length of each string is m . The requested string a and the required Hamming distance k .
The task is reduced to finding all the lines that are within the distance k .
In the original concept of the algorithm, two variants of the problem are considered: static and dynamic.
- In the static task, the distance k is predefined.
- In dynamic, on the contrary, the required distance is not known in advance.
The article describes the solution only static problem.
This implementation focuses on finding strings within k <= 10.
There are three solutions to the static problem: linear search (linear scan), query expansion (query expansion) and database expansion (table expansion).
In this case, the expansion of the request means the generation of all possible variants of lines that fit into a given distance for the original line.
Expanding a database involves creating multiple copies of this database, where either all possible options are generated that meet the requirements of the required distance, or the data is processed in some other way (more on this in more detail.).
HEngine [8] uses a combination of these three methods to effectively balance memory and execution time.
The algorithm is based on a small theorem that says the following:
If for two lines a and b the distance HD ( a , b ) <= k , then if you divide the lines a and b into substrings using the rcut method using the segmentation factor
r > = ⌊ k / 2⌋ + 1
there must be at least q = r - ⌊ k / 2⌋ substrings when their distance does not exceed one, HD ( a i, b i) <= 1.
The selection of substrings from the base line using the rcut method is performed according to the following principles:
A value called a segmentation factor that satisfies the condition is selected.
r > = ⌊ k / 2⌋ + 1
The length of the first r - ( m mod r ) substrings will have a length ⌊ m / r ⌋, and the last m mod r substrings ⌈ m / r ⌉. Where m is the length of the string, ⌊ is rounding to the nearest below, and ⌉ rounding to the nearest above.
Now the same thing, just for example:
Two binary strings with length m = 8 bits are given: A = 11110000 and B = 11010001, the distance between them is k = 2.
Select the segmentation factor r = 2/2 + 1 = 2, i.e. there will be 2 substrings of length m / r = 4 bits.
a1 = 1111, a2 = 0000
b1 = 1101, b2 = 0001
If we now calculate the distance between the corresponding substrings, then at least ( q = 2 - 2/2 = 1) one substring will coincide or their distance will not exceed one.
What we see:
HD (a1, b1) = HD (1111, 1101) = 1
and
HD (a2, b2) = HD (0000, 0001) = 1
The substrings of the base string were called signatures .
Signatures or substrings a1 and b1 (a2 and b2, a3 and b3 ..., a r and b r ) are called compatible with each other, and if their number of differing bits is not greater than one, then these signatures are called coincident .
And the main idea of the HEngine algorithm is to prepare the database in such a way as to find matching signatures and then select those lines that are within the required Hamming distance.
We already know that if you correctly divide a string into substrings, then at least one substring will coincide with the corresponding substring, or the number of different bits will not exceed one (the signatures will match).
This means that we do not need to perform a full search through all the rows from the database, but it is required to first find those signatures that match, i.e. substrings will differ by a maximum of one.
But how to search by substrings?
The binary search method should do a good job of this. But it requires the list of strings to be sorted. But we get several substrings from one string. To perform a binary search on a list of substrings, it is necessary that each such list is sorted in advance.
Therefore, this suggests a method for expanding the database, that is, creating several tables, each for its own substring or signature. (Such a table is called a signature table . And the totality of such tables is a set of signatures ).
In the original version of the algorithm, the permutation of substrings is described so that the selected substrings come first. This is done more for ease of implementation and for further optimization of the algorithm:
There is a string A, which is divided into 3 substrings, a1, a2, a3, the full list of permutations will be respectively:
a1, a2, a3
a2, a1, a3
a3, a1, a2
These signature tables are then sorted.
At this stage, after preliminary processing of the database, we have several copies of the sorted tables, each for its own substring.
Obviously, if we want to first find the substrings, it is necessary to obtain signatures from the requested string in the same way that was used when creating signature tables.
We also know that the required substrings differ by a maximum of one element. And to find them you need to use the query expansion method (query expansion).
In other words, it is required for the selected substring to generate all the combinations including this substring itself, at which the difference will be a maximum of one element. The number of such combinations will be equal to the length of the substring + 1.
And then perform a binary search in the corresponding signature table for a full match.
Such actions should be made for all substrings and for all tables.
And at the very end, you will need to filter those lines that do not fit into the specified Hamming distance. Those. perform a linear search on the found lines and leave only those lines that meet the condition HD ( a , b ) <= k .
The authors suggest using the Bloom filter [7] to reduce the number of binary searches.
The Bloom filter can quickly determine if a substring is in the table with a small percentage of false positives. What works faster than a hash table.
If before a binary search for substrings in a table, the filter returns that this substring is not in this table, then there is no point in searching.
Accordingly, you must create one filter for each signature table.
The authors also note that using the Bloom filter in this way reduces the request processing time by an average of 57.8%.
There is a binary string database with a length of 8 bits:
11111111
10,000,001
00111110
The task is to find all the lines where the number of different bits does not exceed 2 to the target line 10111111.
So the required distance is k = 2.
1. Choose a segmentation factor.
Based on the formula, we choose the segmentation factor r = 2 and it means that there will be two substrings from one string in all.
2. Create a set of signatures.
Since the number of substrings is 2, then only 2 tables need to be created:
T1 and T2
3. Save the substrings in the corresponding tables with the reference to the source.
T1 T2
1111 1111 => 11111111
1000 0001 => 10000001
0011 1110 => 00111110
4. Sort the tables. Each separately.
T1
0011 => 00111110
1000 => 10000001
1111 => 11111111
T2
0001 => 10000001
1110 => 00111110
1111 => 11111111
This completes the pre-processing. And proceed to search.
1. Get the signatures of the requested string.
The search string 10111110 is broken into signatures. It turns out 1011 and 1100, respectively, the first for the first table, and the second for the second.
2. We generate all combinations differing on unit.
The number of options will be 5.
2.1 For the first substring 1011:
1011
0 011
1 1 11
10 0 1
101 0
2.2 For the second substring 1100:
1100
0 100
1 0 00
11 1 0
110 1
3. Binary search.
3.1 For all generated variants of the first substring 1011, we perform a binary search in the first table for a full match.
1011
0011 == 0011 => 00111110
1111 == 1111 => 11111111
1001
1010
Found two substrings.
3.2 Now for all variants of the second substring 1100 we perform a binary search in the second table.
1100
0100
1000
1110 == 1110 => 00111110
1101
Found one substring.
4. Combining results into one list:
00111110
11111111
5. Linearly check for compliance and filter out unsuitable by the condition <= 2:
HD (10111110, 00111110) = 1
HD (10111110, 11111111) = 2
Both strings satisfy the condition of difference of no more than two elements.
Although a linear search is being performed at this stage, it is expected that the list of candidates will not be large at all.
Under conditions when the number of candidates will be large, it is proposed to use the recursive version of HEngine.
Figure 1 shows an example of the search algorithm.
For line length 64 and the distance limit is 4, the segmentation factor is 3, respectively, only 3 substrings per line.
Where T1, T2 and T3 are signature tables that contain only substrings B1, B2, B3, 21, 21 and 22 bits long.
The requested string is divided into substrings. Next, a signature range is generated for the corresponding substrings. For the first and second signatures, the number of combinations will be 22. And the last signature gives 23 variants. And finally a binary search is performed.
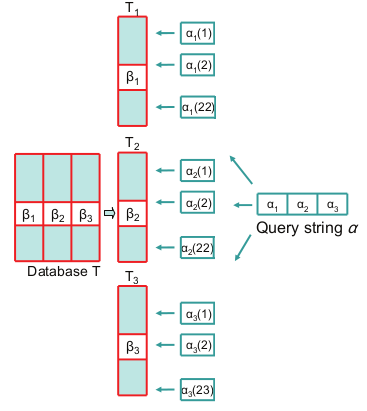
Figure 1. Simplified version of processing requests to signature tables.
The complexity of this algorithm is, on average, O ( P * (log n + 1)), where n is the total number of rows in the database, log n + 1 is a binary search, and P is the number of binary searches: in our case, it is considered the number of combinations per table cleared by the number of tables: P = (64 / r + 1) * r
In extreme cases, the complexity may exceed the linear.
It is noted that this approach uses 4.65 less memory and is 16% faster than the previous work described in [2]. And is the fastest way from now known to find all the lines in a given limit.
All this of course is tempting, but until you touch it in practice, it is difficult to assess the scale.
A prototype of HEngine [9] was created and tested on the available real data.
The results were pleasing, because the search for 343 hashes from the 752420 database takes ~ 0.1 seconds, which is 60 times faster than the linear search.
It would seem that one could stop there. But I really wanted to try to use it somehow in a real project.
There is a database of image hashes, and backend in PHP.
The task was to somehow link the functionality of HEngine and PHP.
It was decided to use FastCGI [10], in this I was greatly helped by posts habrahabr.ru/post/154187 and habrahabr.ru/post/61532 .
From PHP, just call:
That in ~ 0.5 seconds returns the result. When a linear search takes 9 seconds, and through MySQL queries it takes at least 20 seconds.
Thanks to everyone who mastered.
[1] M. Minsky and S. Papert. Perceptrons. MIT Press, Cambridge, MA, 1969.
[2] GS Manku, A. Jain, and AD Sarma. Detecting nearduplicates for web crawling. In Proc. 16Th WWW, May 2007.
[3] ML Miller, MA Rodriguez, and IJ Cox. Audio fingerprinting: The nearest binary search in high-dimensional binary space. In MMSP, 2002.
[4] ML Miller, MA Rodriguez, and IJ Cox. Audio fingerprinting: high resolution binary spaces. Journal of VLSI Signal Processing, Springer, 41 (3): 285–291, 2005.
[5] J. Landr ́e and F. Truchetet. Image retrieval with binary hamming distance. In Proc. 2nd VISAPP, 2007.
[6] H. Yang and Y. Wang. A hammock distance constraint. In Proc. Fourth ICIG, 2007.
[7] B. Bloom. Space / time trade-offs in hash coding with allowable errors. Communications of ACM, 13 (7): 422–426, 1970.
[8] Alex X. Liu, Ke Shen, Eric Torng. Large Scale Hamming Distance Query Processing. ICDE Conference, pages 553 - 564, 2011.
[9] github.com/valbok/HEngine My implementation of HEngine in C ++
[10] github.com/valbok/HEngine/blob/master/bin/fastcgi.cpp Example wrapper program for searching hashes through FastCGI.
Introduction
Hamming distance is the number of different positions for rows with the same length. For example, HD ( 1 0 0 , 0 0 1 ) = 2.
For the first time, the problem of calculating the Hamming distance was posed by Minsky and Papert in 1969 [1], where the task was to search for all the rows from the database that are within the specified Hamming distance to the requested one.
Such a task is unusually simple, but the search for its effective solution still remains on the agenda.
')
Hamming distance is already quite widely used for various tasks, such as finding close duplicates, pattern recognition, document classification, error correction, virus detection, etc.
For example, Manku and associates proposed a solution to the problem of clustering duplicates when indexing web documents based on Hamming distance [2].
Also, Miller and friends suggested the concept of searching songs for a given audio fragment [3], [4].
Similar solutions were used for the task of image search and recognition of the retina [5], [6], etc.
Description of the problem
There is a database of binary strings T , of size n , where the length of each string is m . The requested string a and the required Hamming distance k .
The task is reduced to finding all the lines that are within the distance k .
In the original concept of the algorithm, two variants of the problem are considered: static and dynamic.
- In the static task, the distance k is predefined.
- In dynamic, on the contrary, the required distance is not known in advance.
The article describes the solution only static problem.
Description of the HEngine algorithm for a static task
This implementation focuses on finding strings within k <= 10.
There are three solutions to the static problem: linear search (linear scan), query expansion (query expansion) and database expansion (table expansion).
In this case, the expansion of the request means the generation of all possible variants of lines that fit into a given distance for the original line.
Expanding a database involves creating multiple copies of this database, where either all possible options are generated that meet the requirements of the required distance, or the data is processed in some other way (more on this in more detail.).
HEngine [8] uses a combination of these three methods to effectively balance memory and execution time.
Some theory
The algorithm is based on a small theorem that says the following:
If for two lines a and b the distance HD ( a , b ) <= k , then if you divide the lines a and b into substrings using the rcut method using the segmentation factor
r > = ⌊ k / 2⌋ + 1
there must be at least q = r - ⌊ k / 2⌋ substrings when their distance does not exceed one, HD ( a i, b i) <= 1.
The selection of substrings from the base line using the rcut method is performed according to the following principles:
A value called a segmentation factor that satisfies the condition is selected.
r > = ⌊ k / 2⌋ + 1
The length of the first r - ( m mod r ) substrings will have a length ⌊ m / r ⌋, and the last m mod r substrings ⌈ m / r ⌉. Where m is the length of the string, ⌊ is rounding to the nearest below, and ⌉ rounding to the nearest above.
Now the same thing, just for example:
Two binary strings with length m = 8 bits are given: A = 11110000 and B = 11010001, the distance between them is k = 2.
Select the segmentation factor r = 2/2 + 1 = 2, i.e. there will be 2 substrings of length m / r = 4 bits.
a1 = 1111, a2 = 0000
b1 = 1101, b2 = 0001
If we now calculate the distance between the corresponding substrings, then at least ( q = 2 - 2/2 = 1) one substring will coincide or their distance will not exceed one.
What we see:
HD (a1, b1) = HD (1111, 1101) = 1
and
HD (a2, b2) = HD (0000, 0001) = 1
The substrings of the base string were called signatures .
Signatures or substrings a1 and b1 (a2 and b2, a3 and b3 ..., a r and b r ) are called compatible with each other, and if their number of differing bits is not greater than one, then these signatures are called coincident .
And the main idea of the HEngine algorithm is to prepare the database in such a way as to find matching signatures and then select those lines that are within the required Hamming distance.
Database Preprocessing
We already know that if you correctly divide a string into substrings, then at least one substring will coincide with the corresponding substring, or the number of different bits will not exceed one (the signatures will match).
This means that we do not need to perform a full search through all the rows from the database, but it is required to first find those signatures that match, i.e. substrings will differ by a maximum of one.
But how to search by substrings?
The binary search method should do a good job of this. But it requires the list of strings to be sorted. But we get several substrings from one string. To perform a binary search on a list of substrings, it is necessary that each such list is sorted in advance.
Therefore, this suggests a method for expanding the database, that is, creating several tables, each for its own substring or signature. (Such a table is called a signature table . And the totality of such tables is a set of signatures ).
In the original version of the algorithm, the permutation of substrings is described so that the selected substrings come first. This is done more for ease of implementation and for further optimization of the algorithm:
There is a string A, which is divided into 3 substrings, a1, a2, a3, the full list of permutations will be respectively:
a1, a2, a3
a2, a1, a3
a3, a1, a2
These signature tables are then sorted.
Implementation of the search
At this stage, after preliminary processing of the database, we have several copies of the sorted tables, each for its own substring.
Obviously, if we want to first find the substrings, it is necessary to obtain signatures from the requested string in the same way that was used when creating signature tables.
We also know that the required substrings differ by a maximum of one element. And to find them you need to use the query expansion method (query expansion).
In other words, it is required for the selected substring to generate all the combinations including this substring itself, at which the difference will be a maximum of one element. The number of such combinations will be equal to the length of the substring + 1.
And then perform a binary search in the corresponding signature table for a full match.
Such actions should be made for all substrings and for all tables.
And at the very end, you will need to filter those lines that do not fit into the specified Hamming distance. Those. perform a linear search on the found lines and leave only those lines that meet the condition HD ( a , b ) <= k .
Bloom filter
The authors suggest using the Bloom filter [7] to reduce the number of binary searches.
The Bloom filter can quickly determine if a substring is in the table with a small percentage of false positives. What works faster than a hash table.
If before a binary search for substrings in a table, the filter returns that this substring is not in this table, then there is no point in searching.
Accordingly, you must create one filter for each signature table.
The authors also note that using the Bloom filter in this way reduces the request processing time by an average of 57.8%.
Now the same thing, just by example
There is a binary string database with a length of 8 bits:
11111111
10,000,001
00111110
The task is to find all the lines where the number of different bits does not exceed 2 to the target line 10111111.
So the required distance is k = 2.
1. Choose a segmentation factor.
Based on the formula, we choose the segmentation factor r = 2 and it means that there will be two substrings from one string in all.
2. Create a set of signatures.
Since the number of substrings is 2, then only 2 tables need to be created:
T1 and T2
3. Save the substrings in the corresponding tables with the reference to the source.
T1 T2
1111 1111 => 11111111
1000 0001 => 10000001
0011 1110 => 00111110
4. Sort the tables. Each separately.
T1
0011 => 00111110
1000 => 10000001
1111 => 11111111
T2
0001 => 10000001
1110 => 00111110
1111 => 11111111
This completes the pre-processing. And proceed to search.
1. Get the signatures of the requested string.
The search string 10111110 is broken into signatures. It turns out 1011 and 1100, respectively, the first for the first table, and the second for the second.
2. We generate all combinations differing on unit.
The number of options will be 5.
2.1 For the first substring 1011:
1011
0 011
1 1 11
10 0 1
101 0
2.2 For the second substring 1100:
1100
0 100
1 0 00
11 1 0
110 1
3. Binary search.
3.1 For all generated variants of the first substring 1011, we perform a binary search in the first table for a full match.
1011
0011 == 0011 => 00111110
1111 == 1111 => 11111111
1001
1010
Found two substrings.
3.2 Now for all variants of the second substring 1100 we perform a binary search in the second table.
1100
0100
1000
1110 == 1110 => 00111110
1101
Found one substring.
4. Combining results into one list:
00111110
11111111
5. Linearly check for compliance and filter out unsuitable by the condition <= 2:
HD (10111110, 00111110) = 1
HD (10111110, 11111111) = 2
Both strings satisfy the condition of difference of no more than two elements.
Although a linear search is being performed at this stage, it is expected that the list of candidates will not be large at all.
Under conditions when the number of candidates will be large, it is proposed to use the recursive version of HEngine.
Visually
Figure 1 shows an example of the search algorithm.
For line length 64 and the distance limit is 4, the segmentation factor is 3, respectively, only 3 substrings per line.
Where T1, T2 and T3 are signature tables that contain only substrings B1, B2, B3, 21, 21 and 22 bits long.
The requested string is divided into substrings. Next, a signature range is generated for the corresponding substrings. For the first and second signatures, the number of combinations will be 22. And the last signature gives 23 variants. And finally a binary search is performed.

Figure 1. Simplified version of processing requests to signature tables.
results
The complexity of this algorithm is, on average, O ( P * (log n + 1)), where n is the total number of rows in the database, log n + 1 is a binary search, and P is the number of binary searches: in our case, it is considered the number of combinations per table cleared by the number of tables: P = (64 / r + 1) * r
In extreme cases, the complexity may exceed the linear.
It is noted that this approach uses 4.65 less memory and is 16% faster than the previous work described in [2]. And is the fastest way from now known to find all the lines in a given limit.
Implementation
All this of course is tempting, but until you touch it in practice, it is difficult to assess the scale.
A prototype of HEngine [9] was created and tested on the available real data.
tests$ ./matches 7 data/db/table.txt data/query/face2.txt Reading the dataset ........ done. 752420 db hashes and 343 query hashes. Building with 7 hamming distance bound ....... done. Building time: 12.964 seconds Searching HEngine matches ....... found 100 total matches. HEngine query time: 0.1 seconds Searching linear matches ....... found 100 total matches. Linear query time: 6.828 seconds The results were pleasing, because the search for 343 hashes from the 752420 database takes ~ 0.1 seconds, which is 60 times faster than the linear search.
It would seem that one could stop there. But I really wanted to try to use it somehow in a real project.
One click to real use
There is a database of image hashes, and backend in PHP.
The task was to somehow link the functionality of HEngine and PHP.
It was decided to use FastCGI [10], in this I was greatly helped by posts habrahabr.ru/post/154187 and habrahabr.ru/post/61532 .
From PHP, just call:
$list = file_get_contents( 'http://fcgi.local/?' . $hashes ); That in ~ 0.5 seconds returns the result. When a linear search takes 9 seconds, and through MySQL queries it takes at least 20 seconds.
Thanks to everyone who mastered.
Links
[1] M. Minsky and S. Papert. Perceptrons. MIT Press, Cambridge, MA, 1969.
[2] GS Manku, A. Jain, and AD Sarma. Detecting nearduplicates for web crawling. In Proc. 16Th WWW, May 2007.
[3] ML Miller, MA Rodriguez, and IJ Cox. Audio fingerprinting: The nearest binary search in high-dimensional binary space. In MMSP, 2002.
[4] ML Miller, MA Rodriguez, and IJ Cox. Audio fingerprinting: high resolution binary spaces. Journal of VLSI Signal Processing, Springer, 41 (3): 285–291, 2005.
[5] J. Landr ́e and F. Truchetet. Image retrieval with binary hamming distance. In Proc. 2nd VISAPP, 2007.
[6] H. Yang and Y. Wang. A hammock distance constraint. In Proc. Fourth ICIG, 2007.
[7] B. Bloom. Space / time trade-offs in hash coding with allowable errors. Communications of ACM, 13 (7): 422–426, 1970.
[8] Alex X. Liu, Ke Shen, Eric Torng. Large Scale Hamming Distance Query Processing. ICDE Conference, pages 553 - 564, 2011.
[9] github.com/valbok/HEngine My implementation of HEngine in C ++
[10] github.com/valbok/HEngine/blob/master/bin/fastcgi.cpp Example wrapper program for searching hashes through FastCGI.
Source: https://habr.com/ru/post/211264/
All Articles