The problem of glass balls - the solution in general
 The task of a hundred-story house and two glass balls has long been agitated by the online community ( Habrahabr , LJ , forums ). Inquiring minds certainly ask themselves: what to do in the general case when we have n floors and k balls?
The task of a hundred-story house and two glass balls has long been agitated by the online community ( Habrahabr , LJ , forums ). Inquiring minds certainly ask themselves: what to do in the general case when we have n floors and k balls?Say, how many shots (at least approximately) will be needed in the case of n = 2 40 , k = 10?
Combining the information found in the vastness of the network and my own work, I want to present you a post about the key ideas for solving this problem, as well as the main results and interesting observations obtained during the study.
So, we formulate the condition : we have k identical glass balls. If they fall from the “ x ” or higher floor of the “ n ” -storeyed house, they break up; if they fall from the “ x - 1” -th or lower floor, they remain intact. The value of x is unknown and can be any natural number from 1 to n . Required:
1. Determine the smallest number of tests (throws of the ball) for which you can guaranteed to find x (regardless of its value, in the worst case for us).
2. Develop an algorithm that allows you to guaranteedly find x for no more than the above number of tests.
')
Rough estimate of the smallest number of tests
It is easy to distinguish two extreme cases:
A) we only have 1 ball . Then we are forced to throw it in turn from each floor, starting from the first, until it breaks or until we get to the " n - 1" -th floor. If the ball broke on the “ a ” -th floor (1 ≤ a ≤ n - 1), then x = a . If not crashed on " n - 1" -th, then x = n . In the worst case, you will need n - 1 test.
B) we have a lot of balls (namely, k ≥ log 2 n ). Then you can apply
search method "dividing the segment in half"
In the worst case, you will need ⌈log 2 n ⌉ tests and the same number of balls (all of a sudden they will break each throw).We throw the ball from the middle of the house (from the floor with the number ⌈ n / 2⌉, where ⌈ n / 2⌉ is the smallest integer greater than or equal to n / 2). If it has not crashed, we throw it from the middle of the upper half of the building; if it has broken, we throw the second ball from the middle of the lower half of the building, and so on, each time “dividing” the corresponding section of the building in half.
Thus, the smallest number of tests is in the range from ⌈log 2 n ⌉ to n - 1 inclusive. Denote this number by the function f ( n , k ).
For example, for the case of a one-story house and k balls, ⌈log 2 100⌉ = 7, 100 - 1 = 99, which means 7 ≤ f (100, k ) ≤ 99. Generally speaking, the value of f ( n , k ) decreases quite rapidly with increasing k . So, f (100, 1) = 99, f (100, 2) = 14,
f (100, 3) = 9, f (100, 4) = 8, f (100, 5) = f (100, 6) = f (100, 7) = ... = 7.
A remarkable fact: in the case of a one-story house you can find x in seven attempts with only five balls ! That is, the search method “dividing a segment in half” is not a panacea - it is fast, but not always the most optimal in terms of the required number of balls.
Recurrent formula for counting the smallest number of tests
So, how do you find the exact value of f ( n , k )?
In the simplest situations, everything is clear: f ( n , 1) = n - 1 (see case A), f ( n , k ) = ⌈log 2 n ⌉ for k ≥ log 2 n (see case B), in the number f (1, k ) = 0 (if there is only one floor, then it is also the desired one according to the condition of the problem).
Consider the case of n ≥ 2 and k ≥ 2. Suppose that the first test we threw a ball from the “ a ” -th floor, a can be from 1 to n - 1 inclusive (throwing the ball from the “ n ” -th floor is meaningless). There are two possible outcomes:
Exodus 1: The ball crashed. This means that 1 ≤ x ≤ a . We have a unexplored floors, k - 1 balls, i.e. To ensure that x is found, you need to do more f ( a , k - 1) tests.
Exodus 2: the ball did not crash. This means that a + 1 ≤ x ≤ n . We have n - a unexplored floors, k balls, i.e. To ensure that x is found, you need to do more f ( n - a , k ) tests.
As a result, after throwing the ball from the “ a ” -th floor, you may need more max { f ( a , k - 1), f ( n - a , k )} tests to ensure that x is found .
We want to minimize the number of tests, so we take a such that max { f ( a , k - 1), f ( n - a , k )} is the smallest, namely min a {max { f ( a , k - 1) , f ( n - a , k )}}.
Thus, the smallest number of tests is equal to :
f ( n , k ) = 1 + min a {max { f ( a , k - 1), f ( n - a , k )}} (formula 1).
This formula is sufficient to calculate f ( n , k ) for any given n and k , as well as the floor number a ( n , k ) = a , from which to throw the ball - it can be any of those for which the value max { f ( a , k - 1), f ( n - a , k )} reaches a minimum.
Calculation is easy to implement, for example, in Excel .
Who is interested
In column A, starting from the second row, we will write the values of n in order from 1 to the required. In column B in the corresponding rows we write the values of f ( n , 1), in column C - the values of f ( n , 2) and so on; shifting one column to the right means increasing by one the number of balls.
When n = 1, the value of the function f ( n , k ) is zero, therefore we fill the corresponding string with zeros.
Write the formula = A 3 - 1 in cell B3, since f ( n , 1) = n - 1. Copy (or stretch) it down the required number of lines.
In the cell C3 write the formula:
= 1 + MIN (IF (B $ 2: B2> LARGE (C $ 2: C2; $ A $ 2: $ A2); B $ 2: B2; LARGE (C $ 2: C2; $ A $ 2: $ A2)))
and press CTRL + SHIFT + ENTER , i.e. enter the array formula. Copy (or stretch) it to the desired number of rows down and columns to the right.
The values of a ( n , k ) will be calculated in columns to the right of those used to calculate f ( n , k ), according to the same principle: the rows correspond to the value of n , shifting by one column to the right means increasing by one the number of balls.
In the situation as in the screenshot, column H, starting from the third row, is filled with ones, since a ( n , 1) = 1 (see case A, we always throw a single ball from the first floor).
In the cell I3 write the formula:
= MAX ((B $ 2: B2 <C3) * (LARGE (C $ 2: C2; $ A $ 2: $ A2) <C3) * $ A $ 2: $ A2)
and press CTRL + SHIFT + ENTER , i.e. enter the array formula. Copy (or stretch) it to the desired number of rows down and columns to the right.

In column A, starting from the second row, we will write the values of n in order from 1 to the required. In column B in the corresponding rows we write the values of f ( n , 1), in column C - the values of f ( n , 2) and so on; shifting one column to the right means increasing by one the number of balls.
When n = 1, the value of the function f ( n , k ) is zero, therefore we fill the corresponding string with zeros.
Write the formula = A 3 - 1 in cell B3, since f ( n , 1) = n - 1. Copy (or stretch) it down the required number of lines.
In the cell C3 write the formula:
= 1 + MIN (IF (B $ 2: B2> LARGE (C $ 2: C2; $ A $ 2: $ A2); B $ 2: B2; LARGE (C $ 2: C2; $ A $ 2: $ A2)))
and press CTRL + SHIFT + ENTER , i.e. enter the array formula. Copy (or stretch) it to the desired number of rows down and columns to the right.
The values of a ( n , k ) will be calculated in columns to the right of those used to calculate f ( n , k ), according to the same principle: the rows correspond to the value of n , shifting by one column to the right means increasing by one the number of balls.
In the situation as in the screenshot, column H, starting from the third row, is filled with ones, since a ( n , 1) = 1 (see case A, we always throw a single ball from the first floor).
In the cell I3 write the formula:
= MAX ((B $ 2: B2 <C3) * (LARGE (C $ 2: C2; $ A $ 2: $ A2) <C3) * $ A $ 2: $ A2)
and press CTRL + SHIFT + ENTER , i.e. enter the array formula. Copy (or stretch) it to the desired number of rows down and columns to the right.
Search algorithm x
If we know the values of a ( n , k ), then it is easy to describe the search algorithm x in no more than f ( n , k ) tests.
Login: n - the number of floors of the house, k - the number of balls.
Output: x is the number of the required floor.
The beginning of the algorithm.
Step 1. Initialize the variable: x : = 1. Go to step 2.
Step 2. Stop condition: if n = 1, then output x and STOP, otherwise go to step 3.
Step 3. We throw the ball from the floor with the number x - 1 + a ( n , k ). If the ball is broken, then update the values of the variables: n : = a ( n , k ), k : = k - 1.
If the ball is not broken, then update the values of the variables: x : = x + a ( n , k ), n : = n - a ( n , k ). Go to step 2.
The end of the algorithm.
Consider an example of how to find x in seven tests, if we have a hundred floors and five balls. Using the values of a ( n , k ) from a table built in Excel , we will write the numbers of the floors from which we throw the ball,
in case they break all the time:
57 -> 26 -> 11 -> 4 -> 1 (if not crashed, then further) -> 2 (if not crashed, then below) -> 3 .
If, for example, after throwing the ball from the 26th floor it did not crash, we find ourselves in the situation n = 31, k = 4. Then the sequence of throws looks like:
57 -> 26 -> 26 + 15 = 41 -> 26 + 7 = 33 -> 26 + 3 = 29 -> 26 + 1 = 27 (if not crashed, then further) -> 27 + 1 = 28 .
All possible options will not be considered. It can be seen that the algorithm differs from the search method by “dividing the segment in half”.
Explicit formula for counting the smallest number of tests
The main disadvantage of formula 1 is that quite a lot of resources are needed to calculate it. I managed to solve this recurrent formula explicitly on my own only for k = 2 and k = 3 by searching and justifying the patterns in the table of function values. In particular, in the first case, the result is as follows:
f ( n , 2) = ⌈
 ⌉.
⌉.Similar results people received from other considerations: article (author - Stebanoid ). True answer in it
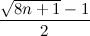 , which is caused by a slightly different condition of the problem - the ball does not have to break when throwing from the very top floor. If we want to take into account this possibility, then in our answer we should substitute the expression n + 1 instead of n (ie, add a floor), and we will get the formula from the article.
, which is caused by a slightly different condition of the problem - the ball does not have to break when throwing from the very top floor. If we want to take into account this possibility, then in our answer we should substitute the expression n + 1 instead of n (ie, add a floor), and we will get the formula from the article.Gradually, however, I came to a dead end, because the general formula could not be found, the recurrence relation is too complicated. It was at this moment that I discovered the wonderful ideas of the users of irishoak , Bert , mikhail_vs and others, which allow us to reduce the calculation of f ( n , k ) to the solution of an interesting inequality.
To do this, we need to consider another function: g ( m , k ) is the largest number of floors, among which you can guaranteedly find x in no more than m tests if there are k balls.
In the simplest situations, the function takes the following values: g ( m , 1) = m + 1 (see case A), g ( m , k ) = g ( m , m ) for k > m (since for m tests you can break at most m balls, the remaining k - m balls are superfluous and do not affect the value of the function).
When m ≥ 2, k ≥ 2, one can derive the recurrence formula:
g ( m , k ) = g ( m - 1, k - 1) + g ( m - 1, k ) (formula 2).
It is easy to understand from the following reasoning:
If we throw a ball from the “ a ” -th floor and it breaks, then we will have m - 1 attempt and k - 1 ball to find x in the range from 1 to a inclusive. For this, a must satisfy the condition: a ≤ g ( m - 1,
k - 1). This means that the highest floor from which we can throw the ball is a = g ( m - 1, k - 1). If it does not break, then we will have m - 1 attempts and k balls, with the help of which we can explore more g ( m - 1, k ) floors. Thus, the maximum will be to investigate the entire g ( m - 1, k - 1) + g ( m - 1, k ) floors.
k - 1). This means that the highest floor from which we can throw the ball is a = g ( m - 1, k - 1). If it does not break, then we will have m - 1 attempts and k balls, with the help of which we can explore more g ( m - 1, k ) floors. Thus, the maximum will be to investigate the entire g ( m - 1, k - 1) + g ( m - 1, k ) floors.
The recurrent formula 2, in contrast to formula 1, is easy to solve, i.e. express g ( m , k ) in explicit form:
g ( m , k ) = C m 0 + C m 1 + C m 2 + ... + C m k ,
where C m i is the number of combinations of m by i , C m i = m ! / ( i ! ( m - i )!).
This equality can be derived "constructively", but you can "guess" and prove it by induction, which is much simpler (here I don’t give proof).
Now to find the smallest number of tests it is required to calculate:
f ( n , k ) = ⌈log 2 n ⌉ for k ≥ log 2 n ,
f ( n , k ) = min {natural m | C m 0 + C m 1 + C m 2 +… + C m k ≥ n } with k <log 2 n .
By the way, when deriving a recurrent formula for g ( m , k ), another way is to determine the number of the floor from which you can throw the ball in order to find x for no more than f ( n , k ) tests: a ( n , k ) = g ( m - 1, k - 1),
where m = f ( n , k ), i.e.
a ( n , k ) = C f ( n , k ) - 1 0 + C f ( n , k ) - 1 1 + C f ( n , k ) - 1 2 +… + C f ( n , k ) - 1 k - 1 for k < f ( n , k ) (formula 3),
a ( n , k ) = 2 f ( n , k ) - 1 for k ≥ f ( n , k ) (formula 4).
Conclusions and adventurous evaluation of the smallest number of tests
Starting the task, I intuitively outlined for myself a solution plan - first understand the principle of finding the right floor (i.e. develop an algorithm), then find how many shots it will require in the worst case.
To my surprise, the way turned out to be different - a rather simple algorithm easily followed from the formulas for calculating the smallest number of tests, which we denoted by f ( n , k ).
Practically knowing nothing about the function f , we roughly estimated it as:
log 2 n ≤ f ( n , k ) ≤ n - 1.
We know that the left boundary is certainly achieved for “large” k , namely, for k ≥ log 2 n , and the right one - for k = 1. We also learned that for intermediate values of k, the search for f ( n , k ) is reduced to finding the least natural m (we denote it by m 0 ) satisfying the inequality:
C m 0 + C m 1 + C m 2 +… + C m k ≥ n (inequality 1).
However, solving it in order to obtain a truly explicit formula for f ( n , k ) seems to be a non-trivial task. It would be interesting to hear your suggestions.
But even if the inequality is not solved, it is possible to estimate the range in which the desired m 0 is located, which is also the value of the function f ( n , k ).
Generally speaking, the presented sum of binomial coefficients can be considered as a polynomial of degree k in variable m . Then finding m 0 from inequality 1 reduces, in fact, to finding the positive roots of the polynomial C m 0 + C m 1 + C m 2 + ... + C m k - n .
There are methods that allow us to estimate the roots of a polynomial, but for this we need to know its coefficients, and in our case they look scary (expressed in eerie sums that are not the fact that they fold). Therefore, we proceed differently.
Let us choose two functions h 1 ( m , k ) and h 2 ( m , k ) so that, first, the inequalities h 1 ( m , k ) ≤ C m 0 + C m 1 + C m 2 + ... + C m k ≤ h 2 ( m , k ), and secondly, for fixed k, the inequalities h 1 ( m , k ) ≥ n and h 2 ( m , k ) ≥ n are easily solved.
It is easy to understand that the solution h 2 ( m , k ) ≥ n will give us an estimate of the desired m 0 from below, and the solution h 1 ( m , k ) ≥ n - from above.
As for the upper estimate of the sum of the binomial coefficients (i.e., the function h 2 ), the best of these is Chernoff's inequality :
C m 0 + C m 1 + C m 2 +… + C m k ≤
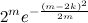 .
.Decision
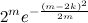 ≥ n gives the following estimate of the smallest number of tests from below :
≥ n gives the following estimate of the smallest number of tests from below :f ( n , k ) ≥
 with k <
with k < 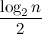 .
.Honestly, I don’t really like this formula - it is bulky and works only for “small” k . But still it is better than our first — rough — assessment, although not always.
Generally speaking, the lower limit of the range is not so important to us, since the value of the function drops rather quickly with increasing k .
Much more interesting to clarify the upper limit. To do this, select h 1 . I did not manage to find any acceptable results on the lower estimate of the sum of the binomial coefficients. Own attempts to invent something led to a funny situation.
Reflecting, I came to the conclusion that C m i ≥
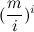 with m ≥ i ≥ 1.
with m ≥ i ≥ 1.Later I found an error in the reasoning, but the inequality still seems to me true, and with a decent margin (as shown by numerical experiments).
It is even more important that not the inequality itself be fulfilled, but
 ≤ C m 0 + C m 1 + C m 2 + ... + C m k , which is even more likely.
≤ C m 0 + C m 1 + C m 2 + ... + C m k , which is even more likely.Unfortunately, this has not yet been formally proved, I will be grateful for suggestive thoughts or references, and possibly counterexamples.
In the end, I decided to continue the study, based on the assumption that my hypothesis is correct, therefore I call the resulting estimate adventurous.
So, h 1 ( m , k ) =
 .
.The inequality h 1 ( m , k ) ≥ n is also not necessarily solved. We know the coefficients for powers of m , so we can estimate the roots of the polynomial h 1 ( m , k ) - n . Using the assessment of Maclaurin , we get that all his positive roots do not exceed
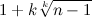 .
.This means that we are looking for m 0 ≤
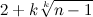 (score 2).
(score 2).In my opinion, a very beautiful formula is compact, depends on both variables in an interesting way, and, most importantly, narrows the range well.
Another way to estimate f ( n , k ) from above is to limit it to f ( n , 2) =
 ⌉. Despite the fact that the number of balls in this formula is not taken into account, sometimes it still gives the best result compared to the estimate 2.
⌉. Despite the fact that the number of balls in this formula is not taken into account, sometimes it still gives the best result compared to the estimate 2.To be sure, we can write the following estimate of the smallest number of tests from above :
f ( n , k ) ≤ min {
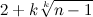 ,
,  + 1}.
+ 1}.Applying the formulas in practice, we obtain, for example, that f (400, 4) lies in the range from 9 to 19, with a real value of 11. Moreover, the right limit of the range is given by estimate 2, while f (400, 2) = 28.
For more extreme values, for example, n = 2 40 , k = 10, we get the left boundary - 58, the right border - 162. For comparison: log 2 n = 40, f ( n , 2) = 1482910, that is, estimate 1 and especially 2 worked very well. The exact value can be found by solving inequality 1, the search gives the answer 76.
Conclusion
Taking into account all the above, it can be stated that the problem of two glass balls in general is solved.
Although no explicit formula for the smallest number of tests has been obtained, it can be determined by solving inequality 1 by brute force or other methods.
Taking into account formulas 3 and 4, this is also sufficient for the operation of a simple algorithm for finding the desired floor.
Analytical calculations (estimates 1 and 2) make it possible to significantly narrow the range in which the smallest number of tests are located, which can be useful in cases where the calculation of the exact value is too time-consuming or is not required.
PS: by the time the post was published, I was able to prove the hypothesis that I used to evaluate 2, namely:
C m i ≥
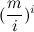 with m ≥ i ≥ 1.
with m ≥ i ≥ 1.Therefore, the assessment is now full, not adventurous.
At the same time, I will still be grateful for references to the literature, where lower estimates for the binomial coefficients or their sum are considered.
Important UPD: In the process of discussing the problem, the user grechnik proposed his own version of the lower and upper estimates of the sum of the binomial coefficients: h 1 ( m , k ) =
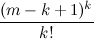 and h 2 ( m , k ) =
and h 2 ( m , k ) = 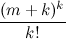 .
.Clarify
We show that h 1 ( m , k ) ≤ C m 0 + C m 1 + C m 2 +… + C m k ≤ h 2 ( m , k ). This follows from the chain of inequalities:
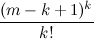 ≤
≤  = C m k ≤ C m 0 + C m 1 + C m 2 +… + C m k ≤ 1 + m +
= C m k ≤ C m 0 + C m 1 + C m 2 +… + C m k ≤ 1 + m + 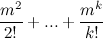 ≤
≤ 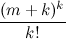 .
.
The last inequality is true, since the coefficients with powers of m on the left side are not greater than on the right side (for m l, on the left side, the coefficient is , and on the right:
, and on the right: 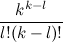 ).
).
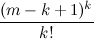 ≤
≤  = C m k ≤ C m 0 + C m 1 + C m 2 +… + C m k ≤ 1 + m +
= C m k ≤ C m 0 + C m 1 + C m 2 +… + C m k ≤ 1 + m + 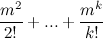 ≤
≤ 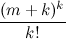 .
.The last inequality is true, since the coefficients with powers of m on the left side are not greater than on the right side (for m l, on the left side, the coefficient is
 , and on the right:
, and on the right: 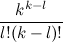 ).
).Now we can estimate the smallest number of tests as:
 - k ≤ f ( n , k ) ≤
- k ≤ f ( n , k ) ≤  + k .
+ k .This means that the smallest number of tests is equal to
 with an accuracy of plus / minus number equal to the number of balls! Great, awesome formula!
with an accuracy of plus / minus number equal to the number of balls! Great, awesome formula!In the comments, users grechnik and Mrrl also offer interesting asymptotic estimates for the value f ( n , k ).
Source: https://habr.com/ru/post/211200/
All Articles