Algorithms of logic of the bot for the game "Minesweeper"
Probably each of us ever played, or at least tried to play “Minesweeper” (“MineSweeper”). The logic of the game is simple, but at one time they even promised a reward for the algorithm of its passing. In my bot, logic has three algorithms that are used depending on the situation on the field. The basic algorithm allows you to find all the cells with a 100% and 0% probability of finding a mine. Using only this algorithm and opening random cells at random in the absence of a reliable solution in a standard sapper at the “Expert” level, 33% of winnings can be achieved. However, some additional algorithms allow you to raise this value to 44% (Windows 7).
The basic algorithm is as follows. Unknown cells (Cell class) adjacent to one open cell are formed into a group (Group class), into which the value of the cell to which it is also attached is written.
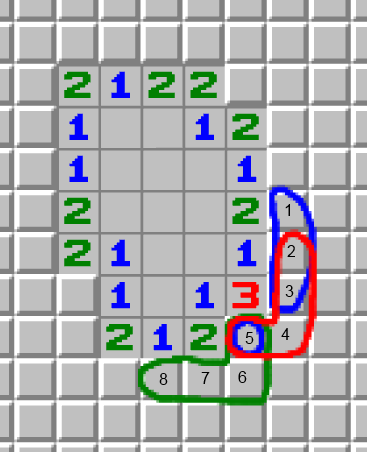
The figure shows four groups, some of which intersect, and some even contain other groups. We denote (123,1) - the group consists of cells 1,2 and 3, and there is 1 mine in them. (5678.2) - in four cells there are 2 mines.
First you need to convert groups. For this:
As a result, we get three types of groups.
')
But often there are situations when there is no reliable solution to the situation. Then the following algorithm comes to the rescue. Its essence is to use the theory of probability. The algorithm works in two stages:

To calculate the probability of finding a mine in a cell next to several open cells, we use the formula for calculating the probability of at least one event:

However, it should be remembered that the sum of probabilities in each group of cells must be equal to the number of mines in the group. Therefore, all values in each group need to be multiplied so that in the end their sum equals the number of minutes. This number is equal to the number of mines in the group divided by the current sum of the probabilities of the cells of the group:
Now those cells that had a probability of 0.57 have 0.485, and those that 0.69 → 0.618
A similar calculation for the second group is carried out taking into account the adjustment from the previous one.
We see that the probability in common cells has changed again, so this adjustment for each group needs to be repeated several times until the system comes to some stable values, which will be the true probabilities of finding mines in the cells.
… etc.

It remains only to choose one of the cells with a minimum probability and make a move.
At the final stage of the game, the number of unmarked mines plays an important role. Knowing this amount, you can enumerate them in unknown cells, and mark the appropriate options. In the process of searching for suitable options for each cell count the number of marks. Dividing the resulting values by the total number of marks, we obtain the probability of finding the min for each cell. For example, in this situation, which seemed to have only one reliable solution, the last method (LastTurns) found 3 cells with a 0% probability of finding a mine.

LastTurns (9.21) checked 144 suitable combinations of 293930 possible and found 3 cells with a minimum probability of 0%
From the point of view of the complexity of understanding an idea, this method is the easiest, so I will not analyze it in detail yet.
In practice, with a sufficient number of samples, the calculated and actual values of the probabilities of finding a mine in a cell almost coincide. The following table shows the results of the bot on the Minesweeper under Windows XP for one night, where
A large discrepancy in the region of 20–22% is probably due to the fact that often this percentage had cells that did not have a number already open (for example, at the beginning of the game), and Minesweeper adjusted to the player, sometimes removing the mine from under the opened cell. The algorithm of work was implemented on java and tested on standard Windows sapper (7 and XP), application in VK and on gameplay. By the way, after several days of “technical problems” when accessing my account from my IP, the game changed the remuneration rules for opening part of the field: initially returned 10% of the rate for 10% of the open field, then 5%, then 2%, and when I stopped playing, then returned 5%.
Main algorithm
The basic algorithm is as follows. Unknown cells (Cell class) adjacent to one open cell are formed into a group (Group class), into which the value of the cell to which it is also attached is written.

The figure shows four groups, some of which intersect, and some even contain other groups. We denote (123,1) - the group consists of cells 1,2 and 3, and there is 1 mine in them. (5678.2) - in four cells there are 2 mines.
First you need to convert groups. For this:
- Compare each group with each subsequent group.
- If the groups are the same, then the second one is deleted.
- If one group contains the other, then subtract the larger from the larger one. That is, there were two groups (5678.2) and (5.1), it became (678.1) and (5.1); (2345.3) and (5.1) → (234.2) and (5.1)
- Intersecting groups, for example (123.1) and (234.2), are transformed according to the following principle:
- Create a new group of intersecting cells (23 ,?)
- We calculate the number of mines in the new group, equal to the number of mines in the group with a large number of mines (234.2) minus the remaining number of cells in another group after the separation of intersecting cells (1 ,?). That is 2-1 = 1. We receive (23,1)
- If the calculated number of mines in the new group (23.1) is not equal to the number of mines in the group with a smaller number of mines (123.1), then stop the conversion
- Subtract the newly formed group from both intersecting groups. (123.1) - (23.1) = (1.0), (234.2) - (23.1) = (4.1).
- Add a newly formed group to the list of groups
- Repeat from step 1 until no changes are made.
Group creation and conversion method
/** * , , , . */ private void setGroups() { groups.clear(); for (int x = 0; x < width; x++) for (int y = 0; y < height; y++) field[x][y].setGroup(groups); // boolean repeat; do{ repeat=false; for (int i = 0; i < groups.size() - 1; i++) { // Group groupI = groups.get(i); for (int j = i + 1; j < groups.size(); j++) { // Group groupJ=groups.get(j); if (groupI.equals(groupJ)) // {groups.remove(j--);break;} Group parent; // Group child; // if (groupI.size()>groupJ.size()) // - {parent=groupI;child=groupJ;} else {child=groupI;parent=groupJ;} if (parent.contains(child)) { // parent.subtraction(child); // repeat=true; // } else if (groupI.overlaps(groupJ) > 0) { // if (groupI.getMines()>groupJ.getMines())// - {parent=groupI;child=groupJ;} else {child=groupI;parent=groupJ;} Group overlap = parent.getOverlap(child);// if (overlap != null) { // ( 0% 100%) groups.add(overlap); // parent.subtraction(overlap); child.subtraction(overlap); repeat=true; } } } } } while(repeat); } As a result, we get three types of groups.
- min number is zero
- the number of mines is equal to the number of cells in the group
- a non-zero number of mines is less than the number of cells in the group
')
If there is no reliable solution
But often there are situations when there is no reliable solution to the situation. Then the following algorithm comes to the rescue. Its essence is to use the theory of probability. The algorithm works in two stages:
- Determination of probability in individual cells, taking into account the effect of several open cells
- Adjustment of probabilities, taking into account the mutual influence of groups with common cells on each other

To calculate the probability of finding a mine in a cell next to several open cells, we use the formula for calculating the probability of at least one event:
The probability of an event A, consisting in the occurrence of at least one of the events 1 , 2 , ..., n , independent in aggregate, is equal to the difference between the unit and the product of the probabilities of opposite events. A = 1- (1-A 1 ) * (1-A 2 ) * .... * (1-A n )In adjacent cells after applying this formula, the result is 1- (1-0,57) * (1-0,28) = 0,69.

However, it should be remembered that the sum of probabilities in each group of cells must be equal to the number of mines in the group. Therefore, all values in each group need to be multiplied so that in the end their sum equals the number of minutes. This number is equal to the number of mines in the group divided by the current sum of the probabilities of the cells of the group:
4 / (0.57 + 0.57 + 0.57 + 0.69 + 0.69 + 0.69 + 0.69) = 0.895
0.57 * 0.895 = 0.485 0.69 * 0.895 = 0.618
Now those cells that had a probability of 0.57 have 0.485, and those that 0.69 → 0.618
A similar calculation for the second group is carried out taking into account the adjustment from the previous one.
2 / (0.28 + 0.28 + 0.28 + 0.618 + 0.618 + 0.618 + 0.618) = 0.604
0.28 * 0.604 = 0.169 0.618 * 0.604 = 0.373
We see that the probability in common cells has changed again, so this adjustment for each group needs to be repeated several times until the system comes to some stable values, which will be the true probabilities of finding mines in the cells.
4 / (0.485 + 0.485 + 0.485 + 0.373 + 0.373 + 0.373 + 0.373) = 1.357
0.485 * 1.357 = 0.658 0.373 * 1.357 = 0.506
2 / (0.169 + 0.169 + 0.169 + 0.506 + 0.506 + 0.506 + 0.506) = 0.79
0.169 * 0.79 = 0.134 0.506 * 0.79 = 0.4
… etc.

It remains only to choose one of the cells with a minimum probability and make a move.
This method is in code.
/** * , */ private void correctPosibilities(){ Map<Cell,Double>cells= new HashMap<>(); // , for (Group group : groups){ for (Cell cell: group.getList()){ Double value; if ((value=cells.get(cell))==null) // cells.put(cell,(double) group.getMines()/ group.size()); // else // , cells.put(cell,Prob.sum(value,(double) group.getMines()/ group.size())); } } // , boolean repeat; do{ repeat=false; for (Group group : groups){ // List<Double> prob= group.getProbabilities(); // Double sum=0.0; for (Double elem:prob)sum+=elem; // int mines= group.getMines()*100; // (- ) if (Math.abs(sum-mines)>1){ // , repeat=true; // Prob.correct(prob,mines); // for (int i=0;i< group.size();i++){ // double value= prob.get(i); group.getList().get(i).setPossibility(value); } } } } while (repeat); for (Cell cell:cells.keySet()){ // if (cell.getPossibility()>99)cell.setPossibility(99); if (cell.getPossibility()<0)cell.setPossibility(0); } } Last moves
At the final stage of the game, the number of unmarked mines plays an important role. Knowing this amount, you can enumerate them in unknown cells, and mark the appropriate options. In the process of searching for suitable options for each cell count the number of marks. Dividing the resulting values by the total number of marks, we obtain the probability of finding the min for each cell. For example, in this situation, which seemed to have only one reliable solution, the last method (LastTurns) found 3 cells with a 0% probability of finding a mine.

LastTurns (9.21) checked 144 suitable combinations of 293930 possible and found 3 cells with a minimum probability of 0%
From the point of view of the complexity of understanding an idea, this method is the easiest, so I will not analyze it in detail yet.
Its implementation
/** * . 30 * @return */ public ArrayList<Point> getLastTurns() { int minesLeft = countMinesLeft(); // ArrayList<Cell> unknownCells = getUnknownCells(); // int notOpened = unknownCells.size(); // Integer[] combinations = new Sequence6().getSequensed(minesLeft, notOpened); // ArrayList<String> list = new ArrayList<String>(); // for (int i = 0; i < combinations.length; i++) { // String combination = Integer.toBinaryString(combinations[i]); // , if (combination.length() < notOpened) { // "0" , String prefix = ""; for (int k = combination.length(); k < notOpened; k++) prefix += "0"; combination = prefix + combination; } for (int j = 0; j < notOpened; j++) { // if (combination.charAt(j) == '1') unknownCells.get(j).setMine(); if (combination.charAt(j) == '0') unknownCells.get(j).setUnknown(); } if (test()) list.add(combination); // , } clear(unknownCells); // String[] comb = new String[list.size()]; list.toArray(comb); // , int[] possibilities2 = new int[notOpened]; // , , for (int i = 0; i < comb.length; i++) // possibilities2[] for (int j = 0; j < notOpened; j++) if (comb[i].charAt(j) == '1') possibilities2[j]++; // , 1 int min = Integer.MAX_VALUE; ArrayList<Integer> minIndices = new ArrayList<>(); // possibilities2[] for (int i = 0; i < possibilities2.length; i++) { if (possibilities2[i] == min) minIndices.add(i); if (possibilities2[i] < min) { min = possibilities2[i]; minIndices.clear(); minIndices.add(i); } unknownCells.get(i).setPossibility(100*possibilities2[i]/comb.length); // } double minPossibility = 100.0 * possibilities2[minIndices.get(0)] / comb.length; System.out.println("LastTurns(" + minesLeft + "," + notOpened + ") " + comb.length + " " + combinations.length + " " + minIndices.size() + " " + " " + (int) minPossibility + " %"); ArrayList<Point> result = new ArrayList<Point>(minIndices.size());// for (int index : minIndices) { result.add(unknownCells.get(index).getPoint()); } return result; } Conclusion
In practice, with a sufficient number of samples, the calculated and actual values of the probabilities of finding a mine in a cell almost coincide. The following table shows the results of the bot on the Minesweeper under Windows XP for one night, where
- Estimated%
- The total number of openings of cells with the calculated%
- Number of hits on a mine
- Actual%
| one. | one | 2 | 3 | four | five | 6 | 7 | eight | 9 | ten | eleven | 12 | 13 | 14 | 15 | sixteen | 17 | 18 | nineteen | 20 | 21 | 22 | 23 | 24 | 25 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 31 | 55 | 117 | 131 | 304 | 291 | 303 | 339 | 507 | 435 | 479 | 1201 | 152 | 146 | 118 | 143 | 164 | 141 | 367 | 3968 | 145 | 63 | 47 | 26 | 92 |
| 3 | one | four | 9 | 6 | 20 | nineteen | 27 | 29 | 56 | 43 | 60 | 147 | 15 | 25 | 14 | 20 | 33 | 26 | 65 | 350 | 14 | five | 12 | four | 23 |
| four. | 3 | 7 | 7 | four | 6 | 6 | eight | eight | eleven | 9 | 12 | 12 | 9 | 17 | eleven | 13 | 20 | 18 | 17 | eight | 9 | 7 | 25 | 15 | 25 |
| one. | 26 | 27 | 28 | 29 | thirty | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 18 | ten | 24 | 18 | 9 | eleven | 6 | 135 | eight | 2 | four | 2 | one | 3 | sixteen | 2 | 2 | one | 462 | ||||||
| 3 | one | 9 | 2 | 3 | 3 | 2 | one | 43 | one | 0 | one | 0 | 0 | one | four | one | one | 0 | 210 | ||||||
| four. | five | 37 | eleven | thirty | 33 | 18 | sixteen | 31 | 12 | 0 | 25 | 0 | 0 | 33 | 25 | 50 | 50 | 0 | 45 |
A large discrepancy in the region of 20–22% is probably due to the fact that often this percentage had cells that did not have a number already open (for example, at the beginning of the game), and Minesweeper adjusted to the player, sometimes removing the mine from under the opened cell. The algorithm of work was implemented on java and tested on standard Windows sapper (7 and XP), application in VK and on gameplay. By the way, after several days of “technical problems” when accessing my account from my IP, the game changed the remuneration rules for opening part of the field: initially returned 10% of the rate for 10% of the open field, then 5%, then 2%, and when I stopped playing, then returned 5%.
Source: https://habr.com/ru/post/211188/
All Articles