Probability in algorithms. Yandex lecture
Many algorithms are deterministic - that is, the sequence of their actions depends only on the input data and the program. But what will happen if the algorithm allows random numbers to be used in the course of work?
It turns out that then interesting results become possible, which cannot be achieved with the help of ordinary algorithms. For example, it is possible to build a hash function for which the adversary cannot easily pick up collisions. Or process a large set of numbers and compress it many times, while retaining the ability to check the belonging of numbers to the original set. You can approximately count the number of different elements in the data stream, having only a small amount of additional memory. In this lecture, Maxim Babenko tells the students how exactly this happens.
Suppose we want to come up with a data structure, which in computer science is called an associative table. In this table, pairs of components are written in two columns. The first column is called the “key” and the second is the “value”. The key, for example, can be the name of a person, and the value is his address. Our task is to quickly perform a search on this table: to find a line in the table where a certain key is present, and to give the corresponding value. The option to view the entire table from top to bottom does not suit us, since we want to search quickly. If the number of rows in the table is taken as n, then the search time should be substantially less than n. We believe that in our table all the keys are unique. If the keys were integers, then everything would be simple enough. It would be necessary to create an array in which elements will be indexed with possible key values in the range from zero to m - 1, where m is not too large. This approach is good because with this method of data storage, in order for key k to refer to the corresponding row and find the corresponding value, it is necessary to spend the constant time O (1). The disadvantage of this method is that if, for example, strings are used as keys instead of numbers, you will have to encode these strings with numbers. And with this encoding, the numerical range will be too large.
')
And here hashing comes to our rescue. Suppose we still have a table of size m, but this time m will have nothing to do with what keys we have. The keys here are some kind of integers. How do we, under these conditions, find the position of the key k in the table? Suppose we know a certain function - h (k), called the hash function. It for a given k tells us which cell of m possible contains this key. If you do not consider exactly how the hash function works, then everything looks very simple. But there is a catch. First, we have infinitely many possible key values, and the hash function maps to a finite set. Therefore, of course, when two different keys after applying a hash function fall into the same cell: it is not clear how we can store them at the same time. Such situations are called collisions, and you need to be able to deal with them. There are many ways to fight. One of the simplest, but at the same time quite effective way is to assume that the cells do not contain values, and even for pairs of key - value, but a whole list of pairs. These are all pairs in which the keys, under the action of the hash function, take on some specific value. This is called the resolution of collisions by the chain method.
The key point here is the choice of a hash function. This is what affects performance. If we choose h (k) = 0, then all our hashes will be zero, and in the end we will get one chain in which we will search all the time. It is very slow and unprofitable. But if the values of the hash functions are to some extent random, then this will not happen.
Consider the concept of randomness from the point of view of mathematics, or rather, a discrete version of this concept. Suppose we have a regular hex dice. Throwing it, we generate some randomness. Those. we have a lot of elementary events - Ω. In our case, the elementary event will be the face that will be on top after the cube completely stops. Denote the faces (a, b, c, d, e, f). Next, we need to set the probability distribution: create a function that, for each elementary event, will say what its probability is from zero to one. Since if our cube is even and hex, then the probability of each side should fall to 1/6.
The random variable in our case is any function defined on elementary events. If we enumerate the faces of a cube by numbers from 1 to 6, then the number corresponding to the dropped face will be a random variable.
Now consider the concept of the average random variable. If elementary events we have are entities (a 1 , ..., a n ), and the probabilities assigned to them are (p 1 , ..., p n ), and our function maps elementary events to values (x 1 , ..., x n ), then we call the average a weighted sum of the form x 1 p 1 + x 2 p 2 + ... x n p n . Those. you need to see what values are accepted and with what probabilities, and then average with a coefficient that is equal to the probability of occurrence of one or another elementary event.
The informal meaning of this lemma is this: if a random variable does not have a very large mean, then it often cannot take large values. We consider the formal formulation of the problem and the proof. Let the discrete probabilistic space (Ω, p) and a random variable on it — f * Ω → R 1 be defined. We are interested in the probability of such an event that the random variable has assumed a value greater than or equal to ε, where ε is some positive number.

We turn to the proof. The proved inequality can be rewritten differently:
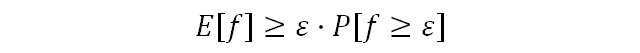
Recall that E [f] = x 1 p 1 + x 2 2 + ⋯ + x n p n . From this we can draw the following conclusion:

After watching the lecture to the end, you will also learn how the above constructions help to build hash functions with a low probability of collisions, and to perform other algorithmic tasks that without the use of random numbers would be impossible or less efficiently solved.
It turns out that then interesting results become possible, which cannot be achieved with the help of ordinary algorithms. For example, it is possible to build a hash function for which the adversary cannot easily pick up collisions. Or process a large set of numbers and compress it many times, while retaining the ability to check the belonging of numbers to the original set. You can approximately count the number of different elements in the data stream, having only a small amount of additional memory. In this lecture, Maxim Babenko tells the students how exactly this happens.
Hash functions
Suppose we want to come up with a data structure, which in computer science is called an associative table. In this table, pairs of components are written in two columns. The first column is called the “key” and the second is the “value”. The key, for example, can be the name of a person, and the value is his address. Our task is to quickly perform a search on this table: to find a line in the table where a certain key is present, and to give the corresponding value. The option to view the entire table from top to bottom does not suit us, since we want to search quickly. If the number of rows in the table is taken as n, then the search time should be substantially less than n. We believe that in our table all the keys are unique. If the keys were integers, then everything would be simple enough. It would be necessary to create an array in which elements will be indexed with possible key values in the range from zero to m - 1, where m is not too large. This approach is good because with this method of data storage, in order for key k to refer to the corresponding row and find the corresponding value, it is necessary to spend the constant time O (1). The disadvantage of this method is that if, for example, strings are used as keys instead of numbers, you will have to encode these strings with numbers. And with this encoding, the numerical range will be too large.
')
And here hashing comes to our rescue. Suppose we still have a table of size m, but this time m will have nothing to do with what keys we have. The keys here are some kind of integers. How do we, under these conditions, find the position of the key k in the table? Suppose we know a certain function - h (k), called the hash function. It for a given k tells us which cell of m possible contains this key. If you do not consider exactly how the hash function works, then everything looks very simple. But there is a catch. First, we have infinitely many possible key values, and the hash function maps to a finite set. Therefore, of course, when two different keys after applying a hash function fall into the same cell: it is not clear how we can store them at the same time. Such situations are called collisions, and you need to be able to deal with them. There are many ways to fight. One of the simplest, but at the same time quite effective way is to assume that the cells do not contain values, and even for pairs of key - value, but a whole list of pairs. These are all pairs in which the keys, under the action of the hash function, take on some specific value. This is called the resolution of collisions by the chain method.
The key point here is the choice of a hash function. This is what affects performance. If we choose h (k) = 0, then all our hashes will be zero, and in the end we will get one chain in which we will search all the time. It is very slow and unprofitable. But if the values of the hash functions are to some extent random, then this will not happen.
Randomness
Consider the concept of randomness from the point of view of mathematics, or rather, a discrete version of this concept. Suppose we have a regular hex dice. Throwing it, we generate some randomness. Those. we have a lot of elementary events - Ω. In our case, the elementary event will be the face that will be on top after the cube completely stops. Denote the faces (a, b, c, d, e, f). Next, we need to set the probability distribution: create a function that, for each elementary event, will say what its probability is from zero to one. Since if our cube is even and hex, then the probability of each side should fall to 1/6.
The random variable in our case is any function defined on elementary events. If we enumerate the faces of a cube by numbers from 1 to 6, then the number corresponding to the dropped face will be a random variable.
Now consider the concept of the average random variable. If elementary events we have are entities (a 1 , ..., a n ), and the probabilities assigned to them are (p 1 , ..., p n ), and our function maps elementary events to values (x 1 , ..., x n ), then we call the average a weighted sum of the form x 1 p 1 + x 2 p 2 + ... x n p n . Those. you need to see what values are accepted and with what probabilities, and then average with a coefficient that is equal to the probability of occurrence of one or another elementary event.
Markov's inequality
The informal meaning of this lemma is this: if a random variable does not have a very large mean, then it often cannot take large values. We consider the formal formulation of the problem and the proof. Let the discrete probabilistic space (Ω, p) and a random variable on it — f * Ω → R 1 be defined. We are interested in the probability of such an event that the random variable has assumed a value greater than or equal to ε, where ε is some positive number.

We turn to the proof. The proved inequality can be rewritten differently:
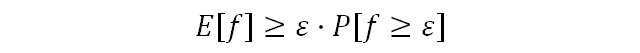
Recall that E [f] = x 1 p 1 + x 2 2 + ⋯ + x n p n . From this we can draw the following conclusion:

After watching the lecture to the end, you will also learn how the above constructions help to build hash functions with a low probability of collisions, and to perform other algorithmic tasks that without the use of random numbers would be impossible or less efficiently solved.
Source: https://habr.com/ru/post/211018/
All Articles