About comparing and optimizing keyboard layouts
This article addresses the issues of analysis and synthesis of keyboard layouts. A comparison of standard and alternative layouts. It also provides one of the possible models for optimizing the layout. This implies standard hard zones for the blind ten-finger dialing method.
Those who are only interested in the model, you can skip the first half of the article.
We will not long describe the traditionally mentioned shortcomings of the YTsUKEN standard layout: 50% of all clicks are made by the index fingers, and often one of them produces several clicks in a row, as well as a significant load on the right pinky. We turn to the characteristics of the next level - the rotation of hands. In my humble opinion (and not only, as will be shown below), this is the most important characteristic affecting the speed of recruitment, since the hands can act independently, and the fingers within each arm move more consistently.
')
The context in which this symbol is located has a significant impact on the convenience and speed of printing a certain character. It is easy to assume that the context is reduced to the location of the key that is pressed before pressing the key with the current character. Although in reality, the convenience of keystroke is influenced not by one key, but by a combination of a certain length (2-3 presses or more, up to several words). Consider the simplest situation. For example, if the previous key was pressed with the other hand, then the time for pressing the next key would be significantly reduced, because Most of the way to the next key can be done simultaneously with the previous movement.
To consider the quality of the YSTUKEN layout, it is according to the criterion of alternation that we will create a summary table characterizing the convenience of recruiting 100 most frequent two-letter combinations according to the data of the National Corpus of the Russian Language ( NCRF ), as well as according to our own calculations. It should be noted that there is some variation in the frequency of individual letters and their combinations depending on the type of text and its volume. But within the most frequent combinations, it is usually insignificant. But one important circumstance follows from this - all calculations based on language statistics, incl. and optimization of layouts should be carried out with an accuracy of a few percent (1-3% is well within the statistical error). If we deduce tenths and hundredths of a percent, then only for some other purposes. Those. Layouts that differ by no more than 1-3% are taken to be equal.
The first column of our table shows the rank of the digram (the number in terms of frequency);
column number 2 - the combination itself;
column number 3 - the frequency of the combination in percent;
Column # 4 - plus is the alternation of hands, if there is none, then the hand indicating the given digram is indicated;
column №5 - numbers of fingers are indicated (1 - index, 2 - middle, 3 - nameless, 4 - little finger, respectively, smaller numbers characterize greater convenience of dialing);
column number 6 - row number (middle row, most convenient for pressing, assigned number 1, top row - number 2, lower, least convenient - number 3, here also smaller numbers are more convenient);
Column No. 7 — summary characteristics of digrams grouped in dozens — relative frequency in percent, the number of digrams dialed with one hand, the amount on the fingers and in rows, characterizing the average convenience.
A total of 20 2-letter combinations for the right hand and 28 for the left. Those. almost half (48%) - on one hand. Apparently, the separation of the most frequent digrams on different hands should give a tangible increase in convenience / speed.
Orange color highlights the fastest combinations (by the sum of fingers and rows no more than 5). Some very fast combinations are used irrationally (for example, several pieces at the end of the first hundred). In part, this may be due to the fact that the inverse (comparable in speed) combination is in the most frequent diagrams (for example, “St” - “tc”). Then the question arises: maybe it is necessary to take the sum of the frequencies responsible for the two combinations (direct and inverse) and determine the correspondence of their frequency of use and speed (convenience of location for pressing)?
Another small note: more rare combinations are leading in the number of combinations per hand, but the dependence is rather non-monotonous. Can I fix something here?
The same non-monotonic dependences are observed on the sums of fingers and rows. Of course, this is not a direct keystroke time, but they have some indirect relation to the speed. Is there room for improvement?
Form the main thesis, which can be taken out of table 1.
There is an opportunity to improve the layout, at least in the first approximation. Most likely, the main improvement should go in the direction of increasing the degree of alternation of hands when typing two-letter combinations and assigning the most frequent combinations to the fastest key pairs.
To once again confirm this thesis, we make up the sum of frequencies for direct and inverse combinations and compare with them the indirect indicators of speed (at least as much in points as for the first table). Note that we are still not going to a good, sustainable optimization rule, but only justify the possibility of improving the layout, starting from its shortcomings. And therefore, approximate estimates and qualitative comparisons will suffice.
If we calculate the share of alternations in all 425 combinations, we get the same value of 205/425 = 48%, i.e. alternations are very rare. If their share could be reduced to at least 75-80%, the speed qualities of the layout would be significantly improved. Suppose that alternating combinations are faster than one-handed at least 20-30%. This corresponds to the real situation, at least on average. Such characteristics were obtained using the Typing Statistics program for estimating the parameters of a set of 20 typesetters with speeds from 500 to 800 dec / min on the website klavogonki.ru .
Then the gain in speed as a whole will be about 7-10%. This is the first opportunity to improve the layout. And, apparently, the main one.
I also recall the period and comma, which are not in the tables mentioned. If they are also separately placed on shortcuts (Shift is automatically removed for a comma), then the speed of the comma will increase by 2 times. Given the frequency of the comma ~ 1%, the total rate will increase by a whole by 0.5% (although these are trifles).
The revision of the zones should also lead to ease of printing, and consequently, to speed. Standard print zones, especially for the left hand and in the production of FWA-OLDJ, are not very convenient. It is advisable to revise them. But this is a topic for a separate work. Apparently, the staging of YVAM TLD is in many cases more comfortable. You can consider other options. Some hands will be quantified below.
Consider the distribution of the number of alternations in dozens of digrams from table 2:
7-7-6-2-4-5-5-4-5-7-7-6-6-7-4-4-4-6-7-7-4-1-3-4-6-6- 3-8-3-5-4-5-4-7-6-4-4-6-5-5-4-3-3- (2).
Let us construct a graph of dozens of frequencies and the number of combinations in them for different hands in order to find out the degree of their mismatch. But even from the above sequence, it is clear that the mismatch is quite strong.
In general, the number of alternations in dozens of digrams fluctuates around a certain average; this type of behavior could be called quasi-random oscillations. The average in this case is about five and there is a weak linear downtrend. The averaged distribution over dozens of combinations is close to uniform with oscillations of considerable amplitude. Those. There is no question of any agreement with frequencies. Here the question arises: is this distribution observed on all hypothetical layouts or can it be improved in the sense of agreement? If it is possible, then this is another way to improve the layout.
In the YTSUKEN layout, as we see, the global distribution mode (eight alternating combinations) generally falls on the 27th decade with very small frequencies.
We form at least at a qualitative level an estimate of the gain, if such a distribution (with the same total number of combinations with alternating hands) is ranked, i.e. number of alternating combinations arranged in descending order. This will be a manual negotiation. Assuming that the rotation of hands accelerates the set by 30% on average, an indirect estimate of the total improvement due to the ranking will be approximately 2%.
In total, we scored 12.5% of the possible increase in speed with average forecasts: 10% due to an increase in the proportion of two-letter combinations recruited with alternating hands, 2% due to the harmonization of frequencies and the number of quick combinations (with alternation), 0.5% for account simplification set comma. Roughly a few percent can be obtained by taking into account other convenient / inconvenient combinations and optimizing the set of other characters. It is not clear how some researchers bring the gain in the transition from QWERTY to Dvorak by several tens of percent, up to 70% (I’ll not give the links now, but I have met similar characteristics somewhere). Surely 70% advantage - only in terms of the path traversed by the fingers when typing. But this is not the most important indicator, and more on that below.
Where else can you look for improvements? As already mentioned, in the arrangement of zones. When transferring the letter K to the middle finger zone, and the letter C to the index finger zone, we will receive a gain both in the convenience of typing (it is not necessary to turn the brush when typing the combination of CS, for example), and in speed (the letter C is more often used than K).
You can also take into account the gain in the redistribution of higher-speed one-armed combinations for more frequent combinations, as well as for combinations with alternation. But since they (one-handed) are still less speedy (than multi-handed), then the gain will not be very large.
Of course, the chosen measure, taking into account the optimization of alternations and one-handed combinations, provides only an indirect estimate. This is without deepening and detailing the nuances. Actually, the optimization criterion is formulated very simply: faster key combinations should correspond to combinations with higher occurrences . It is very difficult to estimate exactly this gain, here only a rough estimation was made, taking into account only the presence / absence of alternation. The real rule should take into account the hand, finger, row, distance to the key (this, by the way, relates directly to the layout selection function, the decisive rule, the objective function — can be called differently). But in general, from the above calculations, it is clear that the YTsUKEN layout is not the worst option. And it seems that theoretically the worst layout from the theoretically best is unlikely to differ by more than 2 times in speed and convenience. From which it can be concluded that the a priori upper estimate (which can never be achieved at all) of the YTsUKEN improvement will be a maximum (and an overestimated maximum), equal, say, to 20%. And even less (according to preliminary data, we obtained only 12.5%).
It is known that in Russian (and, probably, in many European, too), the alternation of vowels and consonants is more common than the combinations of vowel-vowel and consonant-consonant. The question of the statistical relationship of letters in the Russian language was studied by A. A. Markov. According to its results, vowels and consonants alternate in approximately 76.6% of cases.
For a more detailed analysis of the alternation of letters let us compile the following table (frequencies in%).
This suggests a simple rule for building a good alternation of hands layouts: vowels and consonants must fall on different hands. And, apparently, any good layout should use this principle. You can even push it as a criterion for a quick check of the layout for proximity to optimal.
Returning to table 3. It shows that very good properties (unless roughly other criteria are violated) will have a hypothetical layout, on one side of which are vowels and a soft sign, and on the other - all consonants minus a soft sign. But not all vowels and consonants uniquely alternate.
The yellow color indicates combinations where the alternation of a vowel-consonant does not very much dominate over the bunch of vowel-vowel or consonant-consonant (less than 1.5 times). Combinations are shown in red, where such alternation occurs less frequently than the combination of the same name.
For the first four most frequent symbols (O, E, A, I), the alternations clearly dominate, and this is good news, since the greatest load falls on combinations with these letters. And it is here, with the most likely successful combinations, that the foundation for a future good layout is laid.
Next come the consonants H, T. For them, the letters on the left in most cases are still vowels, although they do not so dominate over the consonants. Thus, the relative proportion of alternations will be much less than for the first four letters. This is not very good, since such combinations are also relatively frequent. For letters on the left, the rule of alternation is a consonant-vowel observed in the vast majority of cases. This is a positive thing.
The letter C stands apart. When combined with letters joined at the left, the vowel-consonant alternation is observed in 66% of cases. In the case of letter docking, the trend of alternation is reversed: the consonant-consonant goes in the same 66% of cases. This will affect (within 0.5-0.7% of the speed) the quality of the hypothetical layout, on one side of which there are vowels, and on the other - consonant letters.
It should be said that the option of duplicating letters with the alternation on both sides of the keyboard was considered. The first and most important candidate was the letter "C". But this option had to be abandoned, because There are a lot of letters in Russian, and everything will simply not be located on the main rows of the keyboard. To transfer the letters to the fourth row (digital) or to use the modifier keys for their typing was considered ineffective. Although in the future you can experiment.
In general, the most frequent two-letter combination "ST" is 1.74%. It would seem, therefore, the letters C and T should definitely be spread to different parts of the keyboard, but such a conclusion should be made prematurely at once. Not only this combination determines the convenience of typing letters C or T. It is also necessary to analyze all other combinations with these letters. Only then can we conclude about the convenience of the location of these letters. In our case, the tendencies of alternation of vowels and consonants with the letter C completely balance each other (with an accuracy of 1%), therefore this letter should be placed using some additional criteria (it is possible to use three-letter combinations, take into account the convenience of combinations, hand, finger and etc.). In the first approximation, you can arrange the letter C along with the other consonants.
Then follows a series of consonant letters, for many of which the rules alternate quite often. In these letters, there are three: P, K, P. For them, the letters on the left in most cases are consonants, but for K and P this advantage is rather weak. And in the case of the letter P, the combinations on the left with both vowels and consonants are almost equally probable. When combinations on the right for all these letters, there is a good (from the point of view of the layout in question) value of the fraction of alternations. Then there is a group of five letters, for them the tendency of alternation is not disturbed.
There are three letters in the tail of the frequency distribution, for which alternation is suppressed by the combinations of the same name, but since these letters are quite rare, this does not greatly impair the quality of the layout (0.15% maximum).
It is necessary to make one important remark. So far, we have only considered letters. But there are also character keys (comma, comma, etc.), as well as modifier keys (Shift, etc.). What is the total share of keystrokes of such keys in the total number of keystrokes when typing? First, there is a separator key - a space. Its frequency ranges from 14% to 17.5% (according to various estimates). You can conditionally take 15%.
Further, in Russian punctuation, there are 9 different punctuation marks (for printing):
1. Point (.) Or ellipsis (...) (because they are printed with one key).
2. Comma (,)
3. Dash (-) or hyphen (they are also printed equally in terms of keystrokes)
4. Brackets ()
5. Quotes ("")
6. Question mark (?)
7. Exclamation mark (!)
8. The colon (:)
9. Semicolon (;)
The quotation marks and brackets are distinguishing - they separate out any part of the sentence from the sentence - and are in most cases paired. In this case, the first character is the opening one, the second is the closing one. Other signs have a separating function. They separate sentences, members of a sentence, or parts of a complex sentence from each other.
For completeness, when building a good layout, it is necessary to take into account their frequencies, as well as alternation with different letters or signs. Calculations show that for the point, comma, interrogative and exclamation marks the general rule is fulfilled: after the vowel they follow about 1.4-1.5 times more often than after the consonant. In the standard YTsUKEN layout, a comma and a dot are located on a rather inconvenient key - on the right little finger and the bottom row of the keyboard. In addition, the comma is pressed with Shift. In general, in different texts in the genre, the frequencies of the dot and comma are related differently: in the artistic texts, the frequency of the comma is usually greater, but only slightly. In other genres, there may be a reverse situation. The sum of their frequencies forms a certain invariant, at least on average, regardless of the text genre, approximately equal to 3%.
In addition, you must separately select the Enter key, which highlights the new paragraph (if you analyze only the typing of texts). In addition to paragraphs, this key is entered in dialog boxes, as an alternative to the left mouse button. Those. The frequency of pressing this key can be safely increased to 1%, if we mean the use in various tasks. If we consider it only as a paragraph extractor, then the average frequency of use will be approximately 0.5%.
When typing capital letters, as well as the use of second characters of special keys, use Shift. The frequency of using Shift (lower bound) can be determined from the condition that on average one sentence and one capital letter are on one sentence. Those. The minimum frequency of using Shift will be twice as high as the frequency of using a point (that is, somewhere around 3.0%). In reality, due to proper names and commas, this frequency will be even higher. It may also be worth revisiting the Shift position when building a quasi-optimal layout.
Another frequently used special key is Backspace. She removes typos and performs some other actions. For the average user who owns a blind seal, the error rate is not less than 1%, again, from own practice (for many it is higher, maybe 2% and 3%, and even reach 5% - but this is in very rare cases). This level can be taken as a guideline. And also take into account when optimizing the arrangement of letters / characters on the keyboard.
The total frequency of using the main additional (not alphabetic) keys reaches
15% (Space) +3% (.,) + 1% (Backspace) + 0.5% (Enter) + 0.6% (-) + 0.5% (()) + 0.25% (" ) + 0.15% (?) + 0.07% (!) + 0.07% (:) + 0.02% (;) = 21-22%
even excluding Shift's (i.e., the proportion of the actual letters / characters of the text is 80% or even less). With Shifts taken into account (plus 1.5-3%), this value is close to 24-25%. Quite a tangible value, and it must be considered when building a new layout. Maybe the position of the Shift's should not be changed, since they are arranged symmetrically, and all layouts use them precisely in this quality. On the other hand, it is quite possible to revise Enter and Backspace, since the keys are quite frequency, albeit service.
Let us calculate the relative frequency of the hands alternation relative to the alphabetic part of the hypothetical keyboard (on one hand are all vowels, on the other are all consonants) according to the frequency tables of NCRF digrams. We get 81.1%. This is despite the fact that with the current layout (YTSUKEN), a similar characteristic for the same frequency table of digrams is 54.9%. Those. on the letter part, the new layout is 1.48 times better than YTsUKEN. But we did not take into account that only 75-80% of all characters are letters. Let us try to take this into account, at least approximately, by multiplying the numbers obtained by 0.8, i.e. to the proportion of letters in the text. This is equivalent to the fact that when you press the other keys, the hands alternate altogether (the worst case for the other keys). Those. thus, we define the lower bound of improvement for this particular case:
81.1 * 0.8 = 64.9% - the proportion of alternations, due only to the letter part of the layout, ideal for the alternation of hands;
54.9 * 0.8 = 43.9% - the share of alternations, due only to the letter part of the YTSUKEN layout;
64.9% -43.9% = 21% - the difference in the percentage of alternation of hands, due to the letter part.
In reality, the difference will be even lower. This is due to the fact that for alternations it is necessary to take into account the digrams. And the proportion of pure letter digrams is lower than the proportion of pure letters (70% versus 80%, respectively, but more on that below).
If we keep in mind that alternations improve speed by 30%, then the gain in speed here will be about 21% * 0.3 = 7%. Apparently, this is one of the reasons that alternative layouts provide not a very large actual increase (no more than 20%, according to subjective feelings) of speed and convenience. It is necessary to take into account the alternation of hands when using other keys, incl. service, it is a general picture of the alternations and loads on different fingers and will give the actual percentage of improving the layout.
Those.if the alternation of hands was very rarely used at all, and at the same time they would be loaded fairly evenly, as in the case of normal printing, then when switching to printing with the maximum alternation of hands, the speed would increase by only 30%. (This is assuming that combinations with alternating hands are 30% faster). Thus, an improvement in the layout by 100% (in the sense of alternation) gives an increase in speed by 30%. And the improvement in the layout by 50% is only 15%. A 50% improvement is a very large amount. For this, the initial layout should be very bad (such as alphabetic), and the target layout should be very good (it is generally impossible to achieve 100% alternations or even 90% impossible, if only because even when typing letters, the hands do not always alternate). Then we get the maximum possible hypothetical increase in speed in terms of the increase in the rotation of hands by 80%:
80% * 0.3 = 24%
This is a reasonably well-founded theoretical improvement limit for the worst-case layout speed. Of course, other improvement options are not taken into account, such as alternating fingers in one hand, a set of combinations from the center to the periphery, from the periphery to the center, translation of more frequent letters to faster keys within one hand, etc. But the most significant opportunity to improve layouts - alternating hands, and it gives the maximum possible improvement of 24%.
Many alternative layouts take into account not only the alternation of hands, but also take into account other considerations. In particular, special attention is paid to the distribution of the load between the fingers. In order to identify trends in the development of alternative layouts just by dividing the load into different fingers, a comparative analysis was made of the proportion of keystrokes made by each finger for different layouts (both traditional and alternative for Russian and English).
For the analysis of Russian layouts, we used the results of a statistical analysis of 300 MB of texts in the fiction genre, provided by the user mystes from the site klavogonki.ru . For the analysis of English layouts - site data andong.azurewebsites.net. The calculation results are summarized in table 4.
All or almost all the main existing models for assigning fines when optimizing layouts (such as Klausler, Capewell, QGMLWB, etc.) were analyzed. As a rule, they are not well orthogonalized. Those. one penalty component intersects with the other, taking into account the same circumstance. Example: a “jump” through a row is counted in the distance traveled by the fingers; the same jump is penalized as a difficult combination, although indirectly the same complexity is already taken into account in the distance. But twice to impose a penalty is not necessary. And there are a lot of such nuances.
After a detailed study, the model of fines on andong.azurewebsites.net turned out to be the most acceptable, but it was not finalized. On the other hand, the model http://mkweb.bcgsc.ca/carpalx/ is very well developed, but it only takes distances into account, and does not take into account the costs of keystrokes. For example, when typing characters in the main position, the penalty will be zero. While the physical work is not zero, and the speed is not infinite. The preliminary conclusion is as follows: you need to use a model, the total cost of which will be the sum of the cost of moving your finger to the desired key and the cost of pressing the key. These costs will be subject to rewards and penalties, taking into account convenient / inconvenient combinations.
Let's go back a little, to the analysis of the alternations of hands.
Now, having statistics of digrams, taking into account all characters, and not just letters (NCRF), it is possible to estimate the alternation of hands and using, for example, a space. According to the frequency dictionary , the average word length in the Russian language is 5.28 characters. For each word there is one space (not counting dashes and other characters, separated by a space), i.e. roughly the frequency of the gap can be defined as 1 / (5.28 + 1) = 15.9%. To simplify further approximate calculations we will take 15%.
Diagrams with spaces account for, respectively, about 30% of all digrams, given that the space can be either at the beginning or at the end of the diagram. Then purely letter digrams will be about 70% (ignoring the other characters).
Further suppose that when typing, the “space rule” is observed: the space after the end of a word is always pressed with the other hand. In reality, of course, this rule is not fulfilled by all, and its observance does not affect somehow the speed of dialing or convenience. Rather, it is an attempt to somehow “harmonize” the set so that all fingers are loaded.
To compile a layout with spaces in mind, it is necessary to create a table that will indicate the relative frequencies of the letters representing the beginning and end of the word.
In the calculations, the total number of initial letters was normalized to correspond to the total number of final letters (this is related to the structure of the text, since all words begin with a space - follow it, but not necessarily end with it).
To take into account the alternation of hands when pressing spaces and subsequent keys, it is necessary to consider the hypothetical layout, in which such alternations occur most often, to estimate the gain. Then compare this layout with that already obtained for the criterion of the most frequent alternation of hands when typing letters, and look for a reasonable compromise between them (taking into account the maximization of the total frequency of alternations).
In this case, the maximum alternation of hands after pressing a space will be when the end of the word and the beginning of the next fall on one hand (since the space is always pressed by the opposite hand, compared to the one on which the word has ended). Mathematically, the frequency of interlaces is equivalent to the probability of such an event, and with respect to the total number of digrams, it is written:
30% * {p [lev_nach] * p [lev_kon] + p [gov_nach] * p [prav_kon]},
where p [lev_nach] is the total probability of the beginning of a word from letters on the left hand, p [lev_kon] is the total probability of the word ending on letters that fall on the same left hand; similar for the right hand.
Those. the task is to split the table into two sets of rows and maximize the sum of the products of the post-column sums of probabilities belonging to each of the sets. It sounds a bit cumbersome, but right.
In other words, we first write the same table in a probabilistic form, and then we consider the indicated post-column sums of probabilities, then the products of these sums. Thus, we obtain the probability of alternation with a space for one hand. Do the same for the other. The values obtained for both hands, add. And we strive to maximize this final amount.
Note that this aspect has mostly academic interest, since the rule of alternating spaces in most cases is not respected and the space is pressed with one hand.
Regarding the point and comma, we can say the following. Statistical analysis of large amounts of text (up to several hundred megabytes) shows that the comma and period are more often followed by vowels than by consonants. The same ratio is observed for interrogative and exclamation marks. Approximately 40% of the dots and commas follow after consonants, and in 60% of cases after vowels, respectively. The advantage of vowels in this case is not overwhelming, but it can be taken into account when placing the keys.
The hyphen character (dash) plays the role of a hyphen only in 30% of cases, and in 70% - is a dash, i.e. framed by spaces. After the period and comma follows in 0.1 of all cases of a hyphen, i.e. 0.1 * 30% = 3% of all uses of this symbol.
What is the main difficulty?
Optimization methods (mathematical) are well developed, therefore, the optimization itself is not difficult. The main difficulty is to make the layout quality functional.
What will be the main criterion?
Layouts optimized for speed and comfort are generally two different things. Those.speed layout may not even be ten-finger. The same thing about convenience. But in this case, we are considering the classic method of recruitment.
What is the “blind ten-finger print method (classic) ?:
a) fixed hands;
b) fixed zones - for each finger its own letters;
c) all ten fingers are used (or nine, in case the space is pressed with one thumb).
How to make a model of quality layouts?
a) it is necessary to adequately take into account bad (good) key combinations (separately determine what is “good” or “bad”);
b) choose a compromise between convenience and speed;
c) properly distribute the load on the fingers.
In all these criteria there is some subjectivity, but there are also statements that are accepted by all as true, confirmed with the help of various programs.
For example: pressing keys with different hands, faster in speed than with one hand; set on one row more often faster than on different ones, etc.
It is necessary to collect all possible cases, analyze them, i.e. arrange in order of preference. At the same time, there should not be too many criteria.
Next you need to select the numerical quality assessment. Assume that each key combination assigns some effort in points. Less is better. Here comes subjectivism.
1st subjective choice - which key combinations are good (bad)?
2nd subjective choice - how much better (worse) is this or that combination?
There is one objective criterion - the distance traveled by the fingers from the initial position.
But here it is necessary to take into account that not only the fingers move, but also the hand, i.e. pressing each key is not necessarily from the initial position.
For example: the combination of "ST" - the brush moves to the top row, and then to the bottom. Those.the distance traveled to "T" is greater than from the starting position.
Many optimization models minimize exactly the distance, but this is not the only component, and even far from being the first in importance. The main part of the work falls not on horizontal movements of the fingers, but on keystrokes. And the number of clicks can not be reduced (without automatic replacement ).
Therefore, the main way to improve the layout - minimizing the proportion of uncomfortable combinations, taking into account the distribution of loads on the fingers of each hand.
The cost of pressing each key, according to the previous, will consist of two components: the horizontal movement and the press.
For each finger, cost coefficients for one click and unit of movement are set.
Suppose we chose the coefficients in some way. Next, you need to come up with a system of encouraging good (fast and convenient) combinations and penalizing bad ones.
Suppose we also did this. Now we have a mathematical cost model for typing.
To assess the quality of the layout for the selected model, you need to try (chase away) the layout on any text.
The sample of texts should reflect well the statistical structure of the Russian language and include:
1) a sufficient volume (from several megabytes);
2) different genres (prose, fantasy, scientific texts, journalism), since various combinations of letters and their combinations are used;
3) perhaps even different epochs (classic, modern).
Further, this text is run on the assessment quality assessment model, and the number of points is determined. The layout with the minimum (or maximum, depending on how the model is built) number of points is the best.
But testing the entire multi-megabyte text while testing various layouts is a lengthy exercise, especially since the layouts being tested are millions. Therefore, it is possible to conduct a statistical analysis of the sample and create a table of statistics of n-grams (n-character combinations, n is the desired depth of analysis). In this case, it is no longer necessary to check the entire text, but it is enough to use the statistics table, which is orders of magnitude smaller in size than the source texts. The cost of typing each combination is simply multiplied by the number of repetitions in the text of this combination.
How to choose a quasi-optimal layout, from which set? Obviously, brute force cannot do this, since the number of layouts is N = 33! = 10 64 , taking into account only the permutations of the letters.
It remains to use approximate optimization methods, they are also called heuristic search methods or random / pseudo-random optimization. The main ones I encountered in the analysis of optimization models were:
1) The basic method without any modifications - the Monte Carlo method. The layout is created randomly. We check it in accordance with the model. If it is better for the model than previously calculated, then we take it as the best and create a new layout for testing. Such a method was used by D. Zubachev in the process of searching for his layout.
The other two most commonly used methods are:
2) Imitation annealing method. Used when calculating the QGMLWB layout. Some review of this method can be found here .
3) Genetic method. Used by P. Klausler in calculating his layout. A little introduction is here .
Without further ado, it was decided to use one of the above methods, namely, the annealing method.
Note that the classical method without modifications is quite slow, it has the lowest convergence rate. Therefore, modified optimization methods are commonly used. You also need to consider that all methods of pseudo-random optimization do not guarantee finding the optimal solution, since the number of options is unimaginably large and the probability of getting exactly the best of them is negligible. Of course, in some problems where the “surface of options” has a fairly simple “relief”, you can find a global maximum / minimum, but the task of finding the optimal layout is clearly not one of those.
In the English-language articles on the topic of blind typing, there is information about how they try to take into account the fact that in the process of printing the brush moves, not the fingers. In particular, it is assumed that the neighboring finger of the hand moves in the same direction as the key that is currently pressing, but half the distance (that is, the movements are obtained as if coordinated). Interesting calculations are given in A Theory o Perfomance in skilled typing (BE John, 1996) . In it, the displacement model is supplemented by the finger positioning time, and also the times when the finger is moved up and down (key press / release) are taken into account.
The model of the printing process on three levels is very similar to reality: 1) perception, 2) cognitive, 3) motor. At low print speeds, the throughput of the process (the narrowest point) is dictated by the motor level. And at high (model speed 800 characters / min) - cognitive level. All these models come from the Model Human Processor, in which the work of the brain is modeled by a certain circuit consisting of several discrete components - handlers, buffers, etc.
To take Shift into account when optimizing layouts, it turned out that in some cases there are not enough digram data, and the primary statistics collection algorithm needs to be modified, or it is necessary to restore the missing data, sorting through all the trigrams, etc. Digits with spaces are counted. This is also the load when recruiting. And it will affect the assessment of how profitable this or that layout. Those.spaces should lower the gain of any alternative layout, since they are pressed anyway and for all layouts the same way (if we consider the classic ten-finger dialing method).
The model was taken from the andong.azurewebsites.net site , but with various additions. The total effort (or cost) is made up of two components - pressing a key with each finger and per unit path traveled by each finger. The cost of pressing for little fingers is slightly reduced, because in the original version, they seem disproportionately high.
Costs per press:
2.10 left pinky
1.45 left unnamed
1.05 left middle
1.05 left index
1.00 right index
1.00 right average
1.40 right untitled
2.00 right little finger
1.00 big thumbs
Costs per unit of movement (the key side was taken for the unit):
1.60 left little finger
1.00 left untitled
0.55 left middle
0.75 left index
0.70 right index
0.50 right middle
0.90 right unnamed
1.50 right pinky
As we can see, the odds are somewhat larger for the left hand, which will encourage the use of the right hand in the optimization process. Those.This option is more for right-handers. For left-handers, the coefficients for the right and left hand must be changed.
We should also specify the asymmetry of hand loading. In my opinion, the asymmetry in the number of clicks is 5-10% (that is, if one hand makes 1.05-1.1 times more clicks than the other) does not matter at all.
We see that the cost of pressing taken minimal for index and middle fingers, because they are about equally developed. Perhaps the coefficients for the nameless and little finger should be further reduced.
The cost of movement is minimal for the middle finger, since it is longer than the others. A separate question about the ratio of the cost of moving for the nameless and little fingers. The little fingers are the weakest fingers, but they are more mobile, because these are extreme fingers.
For large fingers, the costs of horizontal movement are absent.
Those.for each key pressed, the costs consisted of two components: the horizontal movement and the pressing. Horizontal displacement may be zero, but total costs will never be zero (as in reality), which explains the choice of such a model as the basis.
For the presentation of a sample of texts, it was decided to use statistics digrams. On the one hand, they are much smaller than the trigrams, which should speed up the optimization process, on the other hand, even the digrams allow you to take into account the main fast / slow combinations, for example, the rotation of hands.
What additional bonuses and penalties need to be charged (i.e., how to encourage convenient, fast digrams and penalize bad ones)? It was decided to introduce the following items:
1. Speed bonus for alternating hands. Perhaps the efforts will not be less when typing a digram with different hands, but the speed on average will be much higher than when typing with one hand. We subtract 60% of the movements for the second letter of the digram (this can be justified by the fact that most of the way to the second letter will be made at the same time as pressing the first one, since in this case the hands move independently). An example of a digram is “SHU”.
2. Movement bonus for agreed motions. Here we need to remember that the fingers do not move independently, but as a whole (the TYPIST model and other works). Those.if the fingers of one hand move to the keys of the same row, then they will travel almost simultaneously. Remove 50% of the movements for the second letter of the digram. Those.in the standard layout, this would be the pressing of the letters "ShG" or "GS" or "SC" or "ES", i.e. standing on the same row (not mainly), but with different fingers.
3. Penalty for pressing the same key. Horizontal displacements for the second letter in the digram are assumed to be zero, since the finger remains above the same position. And we increase the pressure force by 20%. An example is “SS”, “EE”.
4. Penalty for the reverse combination with one hand. If the digram is typed with one hand in the direction from the center of the keyboard to the edge, then the efforts for the second letter both on movements and on pressing increase by 20% (implying a decrease in convenience and speed). An example is “YOU”, “NL”.
5. Penalty for one-finger combinations (excluding repeated pressing of the same letter). The effort to move and press increases by 30% (it is understood that the speed can be significantly reduced). Example - “MA”, “AK”, “OG”, “OT” - in the standard layout there are a lot of such combinations, since 50% of the clicks make the index fingers.
6. Penalty to jump with one hand through a row. Recalling the model of movements, we can say that if there is a jump from the top to the bottom row or vice versa, then the movements to the second letter will be larger than from the starting position. We increase the cost of moving up to the second letter by 50%. Example - "SC", "BSH", "CHU".
7. Fines bottom row. It is believed that on standard keyboards the availability of the lower row is worse than the upper one, therefore it is necessary to enter a complexity factor. For any character in the bottom row, the cost of both moving and pressing increases by 25%.
Some bonuses and penalties may act together. For example, there may be a consistent move to the bottom row, but the digram is typed in reverse order. Those.we get a bonus for the agreed movement and penalties for the bottom row and for the reverse combination with the other hand. An example is “midrange”.
This system of penalties was implemented in the MathCAD package.
The initial data on digrams included all two-character combinations, determined on the basis of an analysis of 300 MB of Russian-language text provided by mystes. As mentioned, pressing Shift's is not taken into account during optimization, since this would require considerable complication, which at first glance is not justified. Accordingly, all capital letters in the statistics were converted to lowercase, and repeating digrams are grouped.
It is necessary to set the layout from which the optimization procedure will start. This layout can be any of the existing, and generated randomly. In our case, the starting layout is the YTsUKEN layout, but with one change - the hard sign and the soft sign are transferred to one key “”, and the comma is replaced by the place “b”. The comma is approximately 1.5% of all characters, and the transfer is done in order to press it without Shift.
Optimization is performed by the annealing method. The optimization step is chosen equal to one permutation of the keys. Do not choose a step too large. This can lead to the fact that the solution will not be close enough to the minimum of the objective function at all. On the other hand, a small step will reduce the rate of convergence. Practice shows that in this case one permutation of keys is a suitable step.
To obtain a reasonable result, the optimization procedure must be performed many times, and then select the best results from the results obtained. This is due to the fact that optimization is stochastic and in most cases will lead to a new result.
The number of iterations for one optimization procedure was chosen to be 1000, 5000, 10000, 50,000, 100,000. As the calculations showed, acceptable results with permissible time costs are provided by the number of iterations 10,000, if you choose from this series.
In order to assess the quality of the layout, not only a force model is used to construct a procedure that defines various characteristics, such as the
proportion of keys of the main row when typing, the
frequency of hands alternation, the
proportion of digrams recruited in reverse order,
the proportion of digrams with coordinated movements, the
proportion of digrams dialed with one finger, the
proportion of diagrams dialed not on adjacent rows with one hand.
Also determined by the breakdown of the load by clicking and moving for each finger. Based on these data, it is possible to make a more reasonable conclusion about the quality of the layout.
Proceeding from the above, optimization as a whole includes the following steps:
1. Load the source file with digram statistics, array preparation (cleaning, converting capital letters to lowercase, grouping).
2. Definition of a matrix of zones for each finger (non-standard zones can also be assigned).
3. Determination of the distance matrix for the zones of claim 2 in relative units.
4. The appointment of two matrices with penalties for moving and pressing for each finger.
5. Assignment of additional bonuses and penalties for various types of digrams.
6. The purpose of the starting layout, the choice of the optimization step, the choice of the number of iterations.
7. Optimization by the annealing method (multiple).
8. Selection of the best layouts.
9. Calculation of additional characteristics of existing Russian-language layouts and optimized layouts.
One of the best results that could be obtained from the point of view of the model described: The
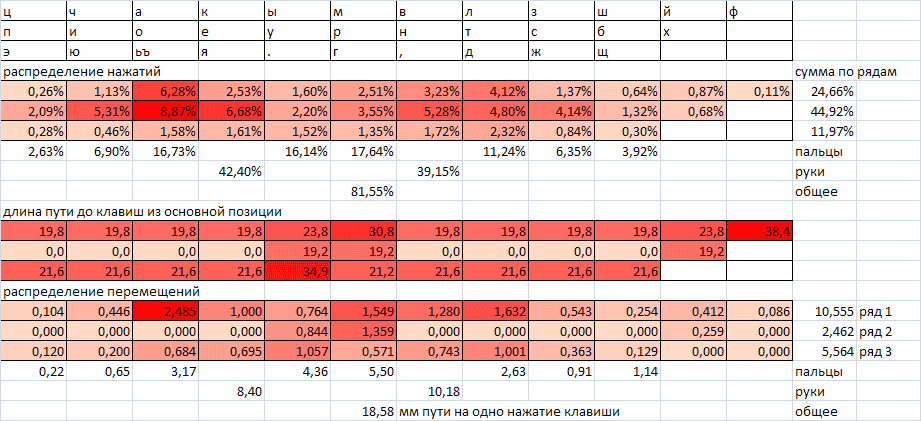
data for loading the fingers in the figure and below can differ, because For optimization, several excellent initial data were used.
The upper row (not in the figure) is corrected manually - the dash is shifted to the number 8. A dash is pressed about 0.8% of all keystrokes and is far ahead of all other punctuation marks, except for the full stop and comma (for which the total is ~ 3%).
This layout provides a total cost equal to 83.5% of the cost of the layout YTSUKEN. As we see, the improvement is not very significant (16.5% by the synthetic criterion), and there is no reason to talk about any huge advantage.
The costs of other layouts with respect to the YTSUKEN layout:
YTZUKEN - 100%;
Speaker - 85.5%;
The layout of D. Zubachev - 86.8%;
Alphabetic - 111.1%.
Those.when taking into account keystrokes, and not just movements, as well as taking into account spaces, the gain becomes not so big at all, within 20%. Determining the gain purely in speed is an even more difficult task.
In one of the articles, The Standard and Dvorak Keyboards Revisited. Direct Measures of Speed (1998) , compares QWERTY and Dvorak. Dvorak is given an advantage in speed of about 4% according to a set of digrams. With the growth of skill, it can reach 10%. But in general, different authors give an advantage in Dvorak's speed from 2% to 7% for a standard skill level. So, there is nothing definite to say about speed, although the gain will obviously be even less than the gain in costs.
Let us assume that the layout, which is minimal for model costs, was obtained. And how to more objectively assess its quality? To increase objectivity, you need to apply other criteria. For example, count such commonly used indicators as hand alternation frequency, the relative number of digits dialed with one finger, the proportion of diagrams recruited in the reverse order, the proportion of digram with jump through a row, the proportion of the main row in the total number of clicks.
The following results were obtained:

Indicators:
1. The proportion of alternations of hands, due only to letter digrams;
2. The proportion of digrams with the agreed movements;
3. The proportion of digits dialed in the reverse order;
4. The proportion of digrams dialed with one finger;
5. The proportion of digrams dialed through the row;
6. The share of clicks on the main row;
7. Costs in relative units per click;
8. The path to the key in relative units (the key size is taken for the unit).
9. Costs for the left hand relative to total costs (excluding the space);
10. The cost of the right hand relative to the total cost (excluding space).
As can be seen, the optimized layout and the Zubachev layout almost coincide in the parameters, with minor variations within 1% for each of the indicators. Moreover, both results were obtained independently, according to different algorithms and according to their criteria. The layouts themselves are of course different. We can say that the optimum is somewhere very close. But which way to optimize is already subjectivism, as well as the choice of the values of fines and rewards.
In addition to the results already obtained, it was decided to search for the best permutations with the minimum number of them, by analogy with carpalx . Those.to find the first best permutation of the keys in the sense of reducing the effort, the second, etc. up to 10-15 permutations. The following results were obtained:
0. Zero permutation (manually) - combining hard and soft signs, and moving a comma to the place .
From this layout we start.
1. W / L (relative improvement relative to the previous layout of 2.8%).
2., / (-2.3%)
3. / (-1.7%)
4. / (-1.7%)
5. / (-1.6%)
6. C /. (-1.3%)
7. U / N (-1.2%)
8. U / L (-1%)
9. D / S (-0.9%)
10. H / F (-0, 5%) at this stage, the force - 1,581.
Parameters were defined for all intermediate options. It turned out that almost all the first replacements of pairs of keys lead only to an improvement in the balancing of efforts on the fingers. At the same time, the main indicators of layouts, such as alternating hands, pressing keys with one finger, etc. may even get worse. Those.The expected result, for example, that described in carpalx with the phased optimization of the English layout, could not be obtained. In this case, the first proposed replacement of E / K leads to an improvement in the alternation of hands and an increase in the frequency of the main position. In our case, the opposite is true. Almost all indicators suffered. Only starting with 5-6 permutations, these indicators begin to improve.
The calculated layout and the layout of D. Zubachev are more consistent with the optimization of the distribution of loads on the fingers. In this case, alternation suffers somewhat, to a greater extent - the frequency of the main position. The proportion of “bad” combinations also increases - backward, one-finger, jumping through a row as a result of an increase in the share of one-armed combinations.
The layout The announcer has a significantly higher proportion of the main position, and the proportion of hands alternating is also slightly higher. The proportion of bad combinations in the amount is very small. Those.The layout is very well done, but using several other criteria and at the cost of some imbalance between the fingers and the hands. For those who do not need good balancing, Announcer is the most acceptable layout.
The study of the new layout for the same areas, as shown by our own experience, is much faster than learning the blind tenfinger method of dialing from scratch. With the experience of recruitment on YTsUKEN 4-5 years, the study of the layout Speaker up to approximately the same speed (> 500 characters / min on texts 300 characters long) occurred in 4.5 months with interruptions ( link ). Further, up to the same speed of 500 zn / min, the layout of D. Zubachev was studied, but already in 2-2.5 months ( link ).
As in all cases of learning a new skill, at the very beginning the speed of learning is the highest, then the growth rate slows down, i.e. the learning curve has an approximately logarithmic form (there is no ceiling, but for each of the next similar increments to speed, it takes several times more time / effort).
But in general, the higher the speed and the longer the experience of typing on the standard layout, the less meaningful the transition to alternative layouts is, unless the standard has very strong inconveniences.
I believe that if the speed reaches 500 characters / min and more on short sections of text, and the work experience on the standard layout is 2-3 years or more, then retraining as a whole does not make much sense. Although, there are also counterexamples , showing that even at high speeds it is possible to relearn and further increase the speed significantly. But mainly it concerns young people (15-25 years old).
In conclusion, we consider another aspect of the applicability of optimization procedures.
Sometimes before the typesetters raises the question of assessing the complexity of the text. Basically, of course, this is purely competitive interest. Suppose one typesetter typed text A at a speed of 700 digits / min, and another - text B at a speed of 650 digits / min. Let the number of corrections in both cases be the same. And the length of the texts is also the same, within the limits of error.
Which of them showed the best result, given that the texts may be of different complexity?
By complexity, in this case, apparently, it is necessary to understand that texts can be composed of words of different frequency, some of which consist of worked out combinations, and others - of poorly worked. In addition, words can be of different lengths, and longer words are harder to perceive and type than standard lengths (4-6 characters). This is the first component of complexity. In the first approximation, you can simply sum up the ranks of words. The final sum (or, let's say, its logarithm) quantifies the complexity of the text.
But there is a second component, let's call it technical - how the fingers move around the keyboard, on which rows they press keys, etc. This is directly related to the layout optimization procedure already described. Only here everything will be done exactly the opposite: if in the process of optimization, different layouts were sorted out on the same language statistics, then to determine the complexity of the text, the layout will be fixed, and the input variable will be the text whose complexity needs to be evaluated.
With increasing skill of the typesetter on a specific layout, the contribution of technical complexity to the overall coefficient of complexity will fall.
In general, the main points when designing layouts were formulated by A. Dvorak (1936) and many other authors, including and modern (in free form):
1) Hand-drawn digrams on average are recruited faster than with one hand;
2) Digrams dialed by the neighboring fingers of one hand are slower than diagrams of fingers spread apart (except for the middle and index fingers);
3) Digrams dialed in the direction of the center-> periphery (from the index to the little finger), slower than in the direction of the periphery-> center;
4) Digrams dialed through a row are slower than diagrams on one row or on adjacent ones;
5) Digrams dialed with one finger are slower than diagrams with different fingers.
To this can add not so much.
Firstly, it is not clear in details what mathematical model was considered when optimizing the layout (meaning A. Dvorak). Which factors are more important and which are minor (although, as was shown above, the result was very good).
Secondly, it is not explicitly taken into account that the fingers belonging to one hand, when the brush is displaced, move all together (the so-called coordinated movements), although there is an echo of this in §2.4. Those.So far, there is no explicit positioning model for the brush when typing. This is a separate very complex task, which is the subject of a separate article. To solve it requires special experiments.
Thirdly, as already mentioned, the context affects the speed of printing a single character. Those.It is possible and necessary to take into account not only digrams, but also trigrams, tetragrams (3-, 4-character combinations), etc., since modern computers allow you to perform similar calculations when optimizing layouts. In general, the trigrams were already taken into account in the carpalx model , where they are divided into several categories according to convenience. But there are no references to which of them are faster and to what extent and by what means the degree of convenience / inconvenience was determined.
Fourth, at the moment there is a very powerful tool for analyzing the various parameters of typing in the face of Typing Statistics(perhaps there are analogues that are unknown to me). It should be noted that A. Dvorak, in developing his principles, also used the TS analog in the form of a paper tape, i.e. could determine the speed of a particular digram. But we must assume that the accuracy of measurement using software methods is now significantly higher.
In summary, the ways to improve the layout optimization model are still not exhausted.
And we note that now almost every student can calculate their own layout, if only they have a computer at hand. Therefore, it is not the fact of the presentation of the new layout that is of particular importance, but the features underlying the mathematical model - how this model differs from the previous ones, what new aspects of the set in it were taken into account, whether it was built on the data on the set of real typesetters, etc.
I thank Vitaly Palyanitsa for the constructive dialogue at the beginning of his work, mystes for the statistical data provided, Dmitry Zubachev for motivation, Maxim Vinokurov for several useful comments, as well as everyone who supported me in the course of my work.
Those who are only interested in the model, you can skip the first half of the article.

Preliminary analysis of possible improvements in the layout JTSUKEN
We will not long describe the traditionally mentioned shortcomings of the YTsUKEN standard layout: 50% of all clicks are made by the index fingers, and often one of them produces several clicks in a row, as well as a significant load on the right pinky. We turn to the characteristics of the next level - the rotation of hands. In my humble opinion (and not only, as will be shown below), this is the most important characteristic affecting the speed of recruitment, since the hands can act independently, and the fingers within each arm move more consistently.
')
The context in which this symbol is located has a significant impact on the convenience and speed of printing a certain character. It is easy to assume that the context is reduced to the location of the key that is pressed before pressing the key with the current character. Although in reality, the convenience of keystroke is influenced not by one key, but by a combination of a certain length (2-3 presses or more, up to several words). Consider the simplest situation. For example, if the previous key was pressed with the other hand, then the time for pressing the next key would be significantly reduced, because Most of the way to the next key can be done simultaneously with the previous movement.
To consider the quality of the YSTUKEN layout, it is according to the criterion of alternation that we will create a summary table characterizing the convenience of recruiting 100 most frequent two-letter combinations according to the data of the National Corpus of the Russian Language ( NCRF ), as well as according to our own calculations. It should be noted that there is some variation in the frequency of individual letters and their combinations depending on the type of text and its volume. But within the most frequent combinations, it is usually insignificant. But one important circumstance follows from this - all calculations based on language statistics, incl. and optimization of layouts should be carried out with an accuracy of a few percent (1-3% is well within the statistical error). If we deduce tenths and hundredths of a percent, then only for some other purposes. Those. Layouts that differ by no more than 1-3% are taken to be equal.
The first column of our table shows the rank of the digram (the number in terms of frequency);
column number 2 - the combination itself;
column number 3 - the frequency of the combination in percent;
Column # 4 - plus is the alternation of hands, if there is none, then the hand indicating the given digram is indicated;
column №5 - numbers of fingers are indicated (1 - index, 2 - middle, 3 - nameless, 4 - little finger, respectively, smaller numbers characterize greater convenience of dialing);
column number 6 - row number (middle row, most convenient for pressing, assigned number 1, top row - number 2, lower, least convenient - number 3, here also smaller numbers are more convenient);
Column No. 7 — summary characteristics of digrams grouped in dozens — relative frequency in percent, the number of digrams dialed with one hand, the amount on the fingers and in rows, characterizing the average convenience.
The beginning of table 1 is here.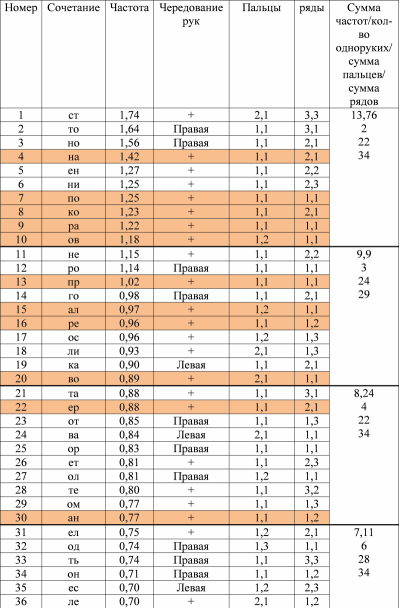

A total of 20 2-letter combinations for the right hand and 28 for the left. Those. almost half (48%) - on one hand. Apparently, the separation of the most frequent digrams on different hands should give a tangible increase in convenience / speed.
Orange color highlights the fastest combinations (by the sum of fingers and rows no more than 5). Some very fast combinations are used irrationally (for example, several pieces at the end of the first hundred). In part, this may be due to the fact that the inverse (comparable in speed) combination is in the most frequent diagrams (for example, “St” - “tc”). Then the question arises: maybe it is necessary to take the sum of the frequencies responsible for the two combinations (direct and inverse) and determine the correspondence of their frequency of use and speed (convenience of location for pressing)?
Another small note: more rare combinations are leading in the number of combinations per hand, but the dependence is rather non-monotonous. Can I fix something here?
The same non-monotonic dependences are observed on the sums of fingers and rows. Of course, this is not a direct keystroke time, but they have some indirect relation to the speed. Is there room for improvement?
Form the main thesis, which can be taken out of table 1.
There is an opportunity to improve the layout, at least in the first approximation. Most likely, the main improvement should go in the direction of increasing the degree of alternation of hands when typing two-letter combinations and assigning the most frequent combinations to the fastest key pairs.
To once again confirm this thesis, we make up the sum of frequencies for direct and inverse combinations and compare with them the indirect indicators of speed (at least as much in points as for the first table). Note that we are still not going to a good, sustainable optimization rule, but only justify the possibility of improving the layout, starting from its shortcomings. And therefore, approximate estimates and qualitative comparisons will suffice.
The beginning of table 2 is here.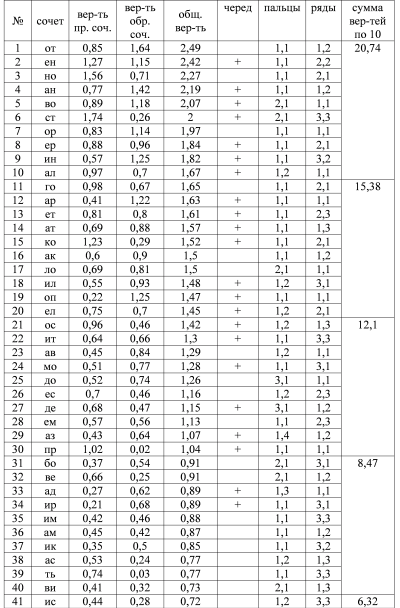

If we calculate the share of alternations in all 425 combinations, we get the same value of 205/425 = 48%, i.e. alternations are very rare. If their share could be reduced to at least 75-80%, the speed qualities of the layout would be significantly improved. Suppose that alternating combinations are faster than one-handed at least 20-30%. This corresponds to the real situation, at least on average. Such characteristics were obtained using the Typing Statistics program for estimating the parameters of a set of 20 typesetters with speeds from 500 to 800 dec / min on the website klavogonki.ru .
Then the gain in speed as a whole will be about 7-10%. This is the first opportunity to improve the layout. And, apparently, the main one.
I also recall the period and comma, which are not in the tables mentioned. If they are also separately placed on shortcuts (Shift is automatically removed for a comma), then the speed of the comma will increase by 2 times. Given the frequency of the comma ~ 1%, the total rate will increase by a whole by 0.5% (although these are trifles).
The revision of the zones should also lead to ease of printing, and consequently, to speed. Standard print zones, especially for the left hand and in the production of FWA-OLDJ, are not very convenient. It is advisable to revise them. But this is a topic for a separate work. Apparently, the staging of YVAM TLD is in many cases more comfortable. You can consider other options. Some hands will be quantified below.
Consider the distribution of the number of alternations in dozens of digrams from table 2:
7-7-6-2-4-5-5-4-5-7-7-6-6-7-4-4-4-6-7-7-4-1-3-4-6-6- 3-8-3-5-4-5-4-7-6-4-4-6-5-5-4-3-3- (2).
Let us construct a graph of dozens of frequencies and the number of combinations in them for different hands in order to find out the degree of their mismatch. But even from the above sequence, it is clear that the mismatch is quite strong.
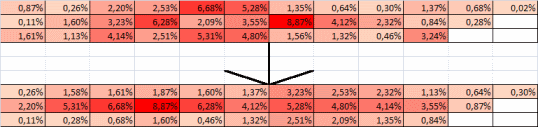
Comparison of frequencies and number of digrams with alternating hands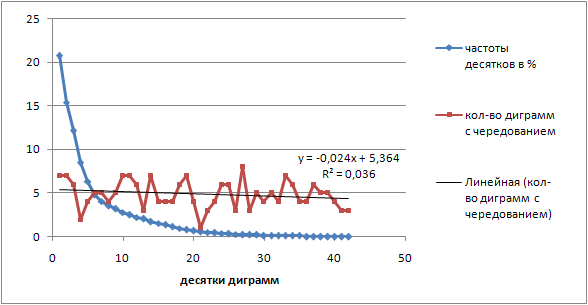

In general, the number of alternations in dozens of digrams fluctuates around a certain average; this type of behavior could be called quasi-random oscillations. The average in this case is about five and there is a weak linear downtrend. The averaged distribution over dozens of combinations is close to uniform with oscillations of considerable amplitude. Those. There is no question of any agreement with frequencies. Here the question arises: is this distribution observed on all hypothetical layouts or can it be improved in the sense of agreement? If it is possible, then this is another way to improve the layout.
In the YTSUKEN layout, as we see, the global distribution mode (eight alternating combinations) generally falls on the 27th decade with very small frequencies.
We form at least at a qualitative level an estimate of the gain, if such a distribution (with the same total number of combinations with alternating hands) is ranked, i.e. number of alternating combinations arranged in descending order. This will be a manual negotiation. Assuming that the rotation of hands accelerates the set by 30% on average, an indirect estimate of the total improvement due to the ranking will be approximately 2%.
In total, we scored 12.5% of the possible increase in speed with average forecasts: 10% due to an increase in the proportion of two-letter combinations recruited with alternating hands, 2% due to the harmonization of frequencies and the number of quick combinations (with alternation), 0.5% for account simplification set comma. Roughly a few percent can be obtained by taking into account other convenient / inconvenient combinations and optimizing the set of other characters. It is not clear how some researchers bring the gain in the transition from QWERTY to Dvorak by several tens of percent, up to 70% (I’ll not give the links now, but I have met similar characteristics somewhere). Surely 70% advantage - only in terms of the path traversed by the fingers when typing. But this is not the most important indicator, and more on that below.
Where else can you look for improvements? As already mentioned, in the arrangement of zones. When transferring the letter K to the middle finger zone, and the letter C to the index finger zone, we will receive a gain both in the convenience of typing (it is not necessary to turn the brush when typing the combination of CS, for example), and in speed (the letter C is more often used than K).
You can also take into account the gain in the redistribution of higher-speed one-armed combinations for more frequent combinations, as well as for combinations with alternation. But since they (one-handed) are still less speedy (than multi-handed), then the gain will not be very large.
Of course, the chosen measure, taking into account the optimization of alternations and one-handed combinations, provides only an indirect estimate. This is without deepening and detailing the nuances. Actually, the optimization criterion is formulated very simply: faster key combinations should correspond to combinations with higher occurrences . It is very difficult to estimate exactly this gain, here only a rough estimation was made, taking into account only the presence / absence of alternation. The real rule should take into account the hand, finger, row, distance to the key (this, by the way, relates directly to the layout selection function, the decisive rule, the objective function — can be called differently). But in general, from the above calculations, it is clear that the YTsUKEN layout is not the worst option. And it seems that theoretically the worst layout from the theoretically best is unlikely to differ by more than 2 times in speed and convenience. From which it can be concluded that the a priori upper estimate (which can never be achieved at all) of the YTsUKEN improvement will be a maximum (and an overestimated maximum), equal, say, to 20%. And even less (according to preliminary data, we obtained only 12.5%).
On the alternation of vowels and consonants
It is known that in Russian (and, probably, in many European, too), the alternation of vowels and consonants is more common than the combinations of vowel-vowel and consonant-consonant. The question of the statistical relationship of letters in the Russian language was studied by A. A. Markov. According to its results, vowels and consonants alternate in approximately 76.6% of cases.
For a more detailed analysis of the alternation of letters let us compile the following table (frequencies in%).
Start of table 3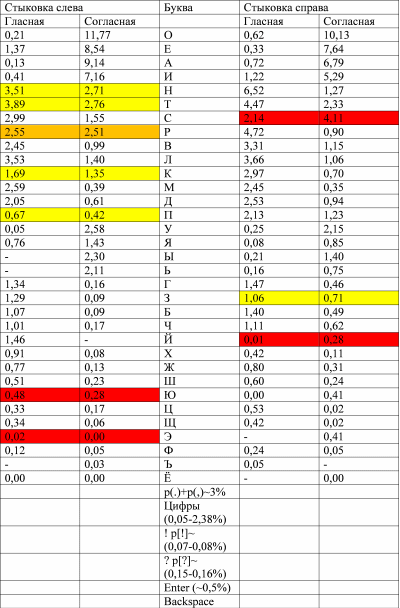

This suggests a simple rule for building a good alternation of hands layouts: vowels and consonants must fall on different hands. And, apparently, any good layout should use this principle. You can even push it as a criterion for a quick check of the layout for proximity to optimal.
A little thought about the alternation of vowels and consonants
The fact that the vowels and consonants alternate follows from the physical features of the acoustic communication channel: source (speech apparatus), transmission medium (air), receiver (ear). If speech consisted only of consonants, then in the presence of external noise it would be very difficult to make out. Vowel sounds add the necessary degree of noise immunity, but at the same time they themselves carry very little information. The main part of the information is transferred by consonant sounds / letters. This can be seen by removing all vowels from the printed text. It is difficult, but it can be disassembled. If you remove the consonants, leaving vowels, then such an operation will be irreversible.
Another purpose of the vowels is to simplify the restructuring of the speech apparatus, to prepare it for pronouncing the new consonant. Those. vowels perform at least two functions.
According to modern ideas about the communication channel, any information produced by the source is compressed to eliminate redundancy (the block where this is done is called the source coder), then this compressed information passes through the channel coder where the redundancy corresponding to the damaging factors of the communication channel is added (noise , fading, etc.). On the receiving side, the signal passes through the channel decoder and the receiver decoder in the same way. From this point of view, the addition of vowels to speech is a noise-resistant coding. You can generally propose a hypothetical binary language consisting of two sounds: 0 or 1 (such language is, in particular, machine), and speak it. But the speech apparatus has more degrees of freedom than speaking out only two sounds. This is the reason for the wealth of the alphabet. Each letter thus carries more information.
Another purpose of the vowels is to simplify the restructuring of the speech apparatus, to prepare it for pronouncing the new consonant. Those. vowels perform at least two functions.
According to modern ideas about the communication channel, any information produced by the source is compressed to eliminate redundancy (the block where this is done is called the source coder), then this compressed information passes through the channel coder where the redundancy corresponding to the damaging factors of the communication channel is added (noise , fading, etc.). On the receiving side, the signal passes through the channel decoder and the receiver decoder in the same way. From this point of view, the addition of vowels to speech is a noise-resistant coding. You can generally propose a hypothetical binary language consisting of two sounds: 0 or 1 (such language is, in particular, machine), and speak it. But the speech apparatus has more degrees of freedom than speaking out only two sounds. This is the reason for the wealth of the alphabet. Each letter thus carries more information.
Returning to table 3. It shows that very good properties (unless roughly other criteria are violated) will have a hypothetical layout, on one side of which are vowels and a soft sign, and on the other - all consonants minus a soft sign. But not all vowels and consonants uniquely alternate.
The yellow color indicates combinations where the alternation of a vowel-consonant does not very much dominate over the bunch of vowel-vowel or consonant-consonant (less than 1.5 times). Combinations are shown in red, where such alternation occurs less frequently than the combination of the same name.
For the first four most frequent symbols (O, E, A, I), the alternations clearly dominate, and this is good news, since the greatest load falls on combinations with these letters. And it is here, with the most likely successful combinations, that the foundation for a future good layout is laid.
Next come the consonants H, T. For them, the letters on the left in most cases are still vowels, although they do not so dominate over the consonants. Thus, the relative proportion of alternations will be much less than for the first four letters. This is not very good, since such combinations are also relatively frequent. For letters on the left, the rule of alternation is a consonant-vowel observed in the vast majority of cases. This is a positive thing.
The letter C stands apart. When combined with letters joined at the left, the vowel-consonant alternation is observed in 66% of cases. In the case of letter docking, the trend of alternation is reversed: the consonant-consonant goes in the same 66% of cases. This will affect (within 0.5-0.7% of the speed) the quality of the hypothetical layout, on one side of which there are vowels, and on the other - consonant letters.
It should be said that the option of duplicating letters with the alternation on both sides of the keyboard was considered. The first and most important candidate was the letter "C". But this option had to be abandoned, because There are a lot of letters in Russian, and everything will simply not be located on the main rows of the keyboard. To transfer the letters to the fourth row (digital) or to use the modifier keys for their typing was considered ineffective. Although in the future you can experiment.
In general, the most frequent two-letter combination "ST" is 1.74%. It would seem, therefore, the letters C and T should definitely be spread to different parts of the keyboard, but such a conclusion should be made prematurely at once. Not only this combination determines the convenience of typing letters C or T. It is also necessary to analyze all other combinations with these letters. Only then can we conclude about the convenience of the location of these letters. In our case, the tendencies of alternation of vowels and consonants with the letter C completely balance each other (with an accuracy of 1%), therefore this letter should be placed using some additional criteria (it is possible to use three-letter combinations, take into account the convenience of combinations, hand, finger and etc.). In the first approximation, you can arrange the letter C along with the other consonants.
Then follows a series of consonant letters, for many of which the rules alternate quite often. In these letters, there are three: P, K, P. For them, the letters on the left in most cases are consonants, but for K and P this advantage is rather weak. And in the case of the letter P, the combinations on the left with both vowels and consonants are almost equally probable. When combinations on the right for all these letters, there is a good (from the point of view of the layout in question) value of the fraction of alternations. Then there is a group of five letters, for them the tendency of alternation is not disturbed.
There are three letters in the tail of the frequency distribution, for which alternation is suppressed by the combinations of the same name, but since these letters are quite rare, this does not greatly impair the quality of the layout (0.15% maximum).
Punctuation marks and service keys
It is necessary to make one important remark. So far, we have only considered letters. But there are also character keys (comma, comma, etc.), as well as modifier keys (Shift, etc.). What is the total share of keystrokes of such keys in the total number of keystrokes when typing? First, there is a separator key - a space. Its frequency ranges from 14% to 17.5% (according to various estimates). You can conditionally take 15%.
Further, in Russian punctuation, there are 9 different punctuation marks (for printing):
1. Point (.) Or ellipsis (...) (because they are printed with one key).
2. Comma (,)
3. Dash (-) or hyphen (they are also printed equally in terms of keystrokes)
4. Brackets ()
5. Quotes ("")
6. Question mark (?)
7. Exclamation mark (!)
8. The colon (:)
9. Semicolon (;)
The quotation marks and brackets are distinguishing - they separate out any part of the sentence from the sentence - and are in most cases paired. In this case, the first character is the opening one, the second is the closing one. Other signs have a separating function. They separate sentences, members of a sentence, or parts of a complex sentence from each other.
For completeness, when building a good layout, it is necessary to take into account their frequencies, as well as alternation with different letters or signs. Calculations show that for the point, comma, interrogative and exclamation marks the general rule is fulfilled: after the vowel they follow about 1.4-1.5 times more often than after the consonant. In the standard YTsUKEN layout, a comma and a dot are located on a rather inconvenient key - on the right little finger and the bottom row of the keyboard. In addition, the comma is pressed with Shift. In general, in different texts in the genre, the frequencies of the dot and comma are related differently: in the artistic texts, the frequency of the comma is usually greater, but only slightly. In other genres, there may be a reverse situation. The sum of their frequencies forms a certain invariant, at least on average, regardless of the text genre, approximately equal to 3%.
In addition, you must separately select the Enter key, which highlights the new paragraph (if you analyze only the typing of texts). In addition to paragraphs, this key is entered in dialog boxes, as an alternative to the left mouse button. Those. The frequency of pressing this key can be safely increased to 1%, if we mean the use in various tasks. If we consider it only as a paragraph extractor, then the average frequency of use will be approximately 0.5%.
When typing capital letters, as well as the use of second characters of special keys, use Shift. The frequency of using Shift (lower bound) can be determined from the condition that on average one sentence and one capital letter are on one sentence. Those. The minimum frequency of using Shift will be twice as high as the frequency of using a point (that is, somewhere around 3.0%). In reality, due to proper names and commas, this frequency will be even higher. It may also be worth revisiting the Shift position when building a quasi-optimal layout.
Another frequently used special key is Backspace. She removes typos and performs some other actions. For the average user who owns a blind seal, the error rate is not less than 1%, again, from own practice (for many it is higher, maybe 2% and 3%, and even reach 5% - but this is in very rare cases). This level can be taken as a guideline. And also take into account when optimizing the arrangement of letters / characters on the keyboard.
The total frequency of using the main additional (not alphabetic) keys reaches
15% (Space) +3% (.,) + 1% (Backspace) + 0.5% (Enter) + 0.6% (-) + 0.5% (()) + 0.25% (" ) + 0.15% (?) + 0.07% (!) + 0.07% (:) + 0.02% (;) = 21-22%
even excluding Shift's (i.e., the proportion of the actual letters / characters of the text is 80% or even less). With Shifts taken into account (plus 1.5-3%), this value is close to 24-25%. Quite a tangible value, and it must be considered when building a new layout. Maybe the position of the Shift's should not be changed, since they are arranged symmetrically, and all layouts use them precisely in this quality. On the other hand, it is quite possible to revise Enter and Backspace, since the keys are quite frequency, albeit service.
End of preliminary stage
Let us calculate the relative frequency of the hands alternation relative to the alphabetic part of the hypothetical keyboard (on one hand are all vowels, on the other are all consonants) according to the frequency tables of NCRF digrams. We get 81.1%. This is despite the fact that with the current layout (YTSUKEN), a similar characteristic for the same frequency table of digrams is 54.9%. Those. on the letter part, the new layout is 1.48 times better than YTsUKEN. But we did not take into account that only 75-80% of all characters are letters. Let us try to take this into account, at least approximately, by multiplying the numbers obtained by 0.8, i.e. to the proportion of letters in the text. This is equivalent to the fact that when you press the other keys, the hands alternate altogether (the worst case for the other keys). Those. thus, we define the lower bound of improvement for this particular case:
81.1 * 0.8 = 64.9% - the proportion of alternations, due only to the letter part of the layout, ideal for the alternation of hands;
54.9 * 0.8 = 43.9% - the share of alternations, due only to the letter part of the YTSUKEN layout;
64.9% -43.9% = 21% - the difference in the percentage of alternation of hands, due to the letter part.
In reality, the difference will be even lower. This is due to the fact that for alternations it is necessary to take into account the digrams. And the proportion of pure letter digrams is lower than the proportion of pure letters (70% versus 80%, respectively, but more on that below).
If we keep in mind that alternations improve speed by 30%, then the gain in speed here will be about 21% * 0.3 = 7%. Apparently, this is one of the reasons that alternative layouts provide not a very large actual increase (no more than 20%, according to subjective feelings) of speed and convenience. It is necessary to take into account the alternation of hands when using other keys, incl. service, it is a general picture of the alternations and loads on different fingers and will give the actual percentage of improving the layout.
Those.if the alternation of hands was very rarely used at all, and at the same time they would be loaded fairly evenly, as in the case of normal printing, then when switching to printing with the maximum alternation of hands, the speed would increase by only 30%. (This is assuming that combinations with alternating hands are 30% faster). Thus, an improvement in the layout by 100% (in the sense of alternation) gives an increase in speed by 30%. And the improvement in the layout by 50% is only 15%. A 50% improvement is a very large amount. For this, the initial layout should be very bad (such as alphabetic), and the target layout should be very good (it is generally impossible to achieve 100% alternations or even 90% impossible, if only because even when typing letters, the hands do not always alternate). Then we get the maximum possible hypothetical increase in speed in terms of the increase in the rotation of hands by 80%:
80% * 0.3 = 24%
This is a reasonably well-founded theoretical improvement limit for the worst-case layout speed. Of course, other improvement options are not taken into account, such as alternating fingers in one hand, a set of combinations from the center to the periphery, from the periphery to the center, translation of more frequent letters to faster keys within one hand, etc. But the most significant opportunity to improve layouts - alternating hands, and it gives the maximum possible improvement of 24%.
Calculation of the load on each finger for different keyboard layouts
Many alternative layouts take into account not only the alternation of hands, but also take into account other considerations. In particular, special attention is paid to the distribution of the load between the fingers. In order to identify trends in the development of alternative layouts just by dividing the load into different fingers, a comparative analysis was made of the proportion of keystrokes made by each finger for different layouts (both traditional and alternative for Russian and English).
For the analysis of Russian layouts, we used the results of a statistical analysis of 300 MB of texts in the fiction genre, provided by the user mystes from the site klavogonki.ru . For the analysis of English layouts - site data andong.azurewebsites.net. The calculation results are summarized in table 4.
Table 4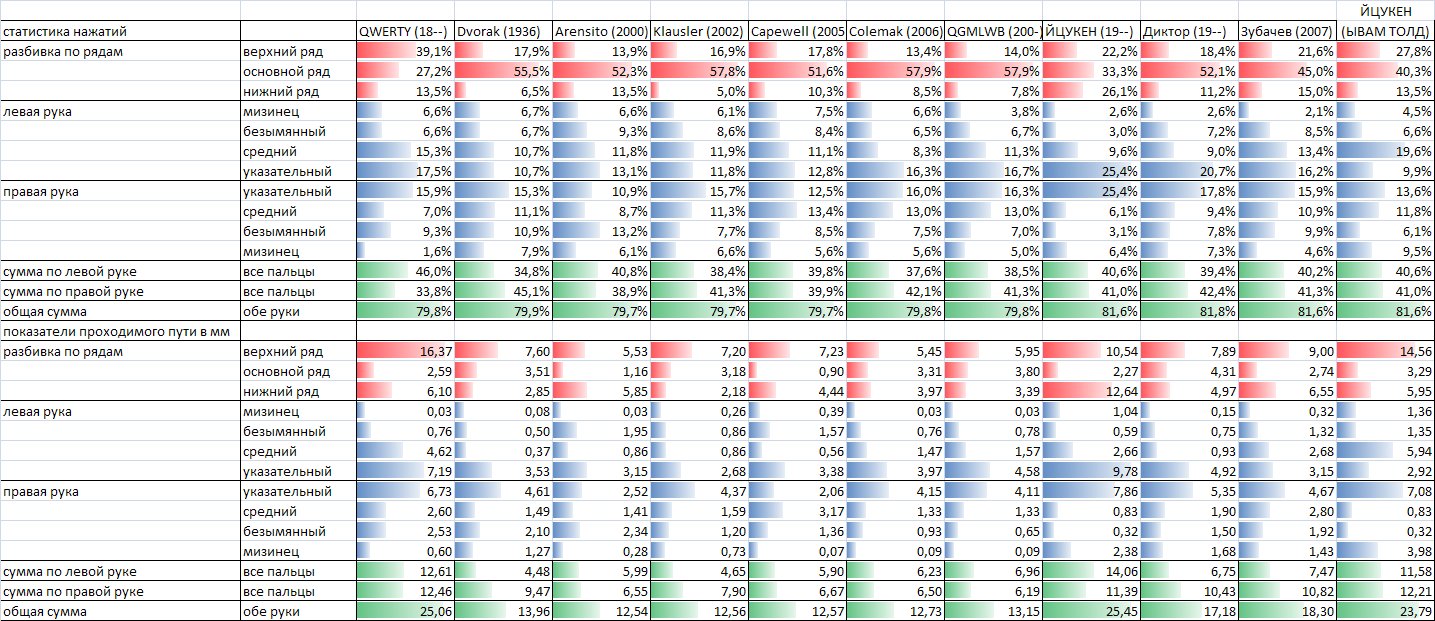

Discussion of the layouts according to table 4
.
QWERTY . – (27%) (39%). (.. ), . 46%/34% = 1,35. Those. 35% . . , . , , , . – 12,61 12,46 – .. . 25 . 4, .
QWERTY: ; , – ; , ; ( , ) – .
Dvorak . – 55,5%. QWERTY. ( ) – 6,5%, .
, , QWERTY. , . – , . , : 35%/45% = 0,78, , 1,28. Those. 28% . , – , . , , – 4,48 9,47 , .. , 2 . , ( ). , . 13,96 . QWERTY 80% (!). , , . , , . , , , , .
ARENSITO . , . 52,3% – . – 13,9% 13,5% – , , .. .
ARENSITO ( Kinesis, Maltron), . ( , Dvorak QWERTY). 13,2% (, – 10,9%), . 40,8%/38,9%=1,05, .. 5%. ( , Dvorak) – . (5,99 6,55 ) 10%- , ( ). Those. - . 12,54 – (, , , ). , Dvorak 11%. ARENSITO . . ARENSITO Dvorak.
, . QWERTY, . Dvorak, . . ARENSITO, , , ( ARENSITO), (ARENSITO ). , .
( Klausler ). 57,8% – . – 5,0% – . , , .
, ( ). , ARENSITO. 38,4%/41,3%=1,075 – 7,5% , . , . , . , 0,86 : , . (4,65 7,98 ), , Dvorak, - 70% . ( ) , , . , . . , Dvorak ( , , ). , , 12,56 – . , . , , Dvorak - . , .
. ( . Capewell ). . , , , . , Dvorak Klausler, , , .
51,6%. , . 10,3% – , ARENSITO, , Klausler.
-, - (.. ), , , ARENSITO Klausler . «» – 13,4%, – 12,5%. 39,8%/39,9%=1 (!). , . , 10% ( , .. ) , , . , , . – QWERTY, .
: , – . Those. . (5,90 , 6,67 ) , 13%. 12,57 – ARENSITO (12,54 ) Klausler (12,56 ).
Colemak . , , 57,9%. ( 0,1% , Klausler, , , ; 2-3% ). – 8,5% – .
, . 16% 5,6% – . : (8,3%), -, , (6,5%) ( 0,1%). , ( , .). 37,6%/42,1%=1,12 ( 12%). – ( , , ). Those. , . (6,23 6,50 ) ( 5%). , , - , , 12,73 . .
– , (, -, , ). Those. . - . , - , , . – ARENSITO. – Capewell. – Dvorak. – Colemak.
QGMLWB . – 57,9%; – 7,8%. .
, , .. . . . . , ( QWERTY, QWERTY , ). – 38,5%/41,3% = 0,93 ( 7% ) – .
Colemak. . , Colemak – 6,96 /6,19 = 1,12. ( Colemak) . , , 13,15 , , .
, , QGMLWB, , , .
.
. 33,3%. , , .. . (26,1% 22,2%), . , , .
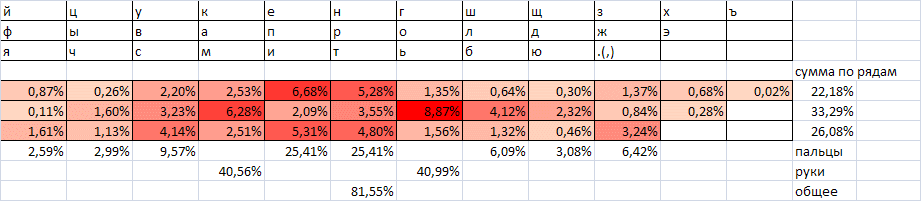
By interdigital balancing of the proportion of clicks, you can immediately say that the index fingers are knocked out - each of them accounts for 25% of the total number of clicks (in total, index fingers account for 50.8% of clicks, on the middle ones - 15.7%, for unnamed - 6.1%, for little fingers - 9%). For those whose index fingers are very well developed, YTsUKEN may even be a very high-speed layout (implying a set of basically two of the most powerful fingers). In general, such a layout should be quite good when working with the mouse, when only one hand rests on the keyboard. But with a blind set is made with two hands, so this plus can be very doubtful. Compared with the index heavily underloaded middle fingers, as well as unnamed. The right little finger is overloaded (even without the Shift and “-” keys). Interdigital balancing is one of the worst. The main load falls on the index. But according to the balance of the share of clicks for the hands, JTSUKEN shows a very good result: 40.6% / 41.0% (asymmetry 1%) - similar to the Capewell indicator, when compared with English-language layouts. By moving the little fingers are very heavily loaded (more than in any of the English-language layouts: they account for 3.42 mm). In other layouts, the movements of the little fingers did not have more than 1-2 mm. It can be noted that the nameless underutilized, and the index perform too much movement. The left hand gives 14.06 mm movements for one press, the right hand - 11.39 mm. Asymmetry is 23% (not a very good indicator, but far from the worst). In general, one click accounts for 25.45 mm - even more than in QWERTY, although a priori it can be assumed that, due to ergonomics, JTSUKEN should take better place among Russian-language layouts than QWERTY among English-language layouts. One of the general conclusions drawn from this point: the ergonomics of the Russian-language layouts, all other things being equal, will be worse than for English-speaking ones.
Layout Announcer . In this layout, a significant optimization has already been made in comparison with JCUKEN. The share of the main series is 52.1%. The share of the bottom row - 11.2%. When considering the share of clicks on each of the fingers, it can be seen that in comparison with YTsUKEN, the balancing of the share of clicks is significantly improved: the unnamed are loaded in accordance with their total share in much the same way as the best examples of English-language layouts. Although the right little finger is heavily loaded - 7.3% (in YTSUKEN it was 6.4%).
But in general, the load on the fingers of each hand decreases rather monotonously. The movements of the fingers of the left hand form a monotonously decreasing sequence, although it would be possible to load the left middle finger more heavily. For the right hand, the sequence also looks quite good, for the middle, ringless, little finger, there are approximately equal movements, with the dominance of the index finger. The right little finger passes 1.68 mm per click (this is less than in YTSUKEN, where there was 2.38 mm). The contribution to the movement of each of the hands is 6.75 mm and 10.43 mm, the asymmetry is very significant at 54%. And the general asymmetry develops, because she encourages the right hand for both pressing and moving. The average horizontal distance traveled by the fingers when you press one key is 17.18 mm, i.e. a very significant improvement over YTsUKEN (by 48%). It is also worth mentioning the frequency of the hands alternations: for YTsUKEN, it is equal to 61.2%, for the speaker’s layout - 76.2%.
The layout of D. Zubachev (links to the discussion of the layout: 1 , 2 ). The share of the main (middle) series by pressing is equal to 45.0%, the share of the lower one - 15.0%. At first glance, not very good performance. But if you look at the interdigital balance by pressing the keys, you can see very good dependencies. Besides the fact that they are monotone, these dependences have a constant change in the transition from finger to finger. And the loads of pairwise sums on the fingers of both hands (both of the index, both of the middle ones, etc.) converge with the partial loads of the fingers of each hand. Those. it can be said that the dependencies for both hands are in good agreement. At the same time, the Zubachev layout also demonstrates a rather small asymmetry of hand presses: 40.2% / 41.3% = 0.97 (asymmetry is less than 3%).
Apparently, the layout is well balanced.
The distribution of the movements on the fingers of each of the hands is subject to monotonous dependence. Finger movements are distributed fairly well, i.e. the total load on the index significantly exceeds the load on the average, etc. decreasing right up to the little fingers. The asymmetry of movement in each of the hands (7.47 mm to 10.82 mm) is 45% - less than in the Announcer, although more than in YTsUKEN. Balancing movements between hands is worse than pressing, but also not very bad (much better, for example, than for Dvorak). The average distance traveled by the fingers when you press one key is 18.30 mm and a little more than for the Speaker layout (by 6.5%). Apparently, here we come to the point that we have already encountered when considering the English-language layouts, after which an improvement in the balancing of the loads on the fingers leads to a more significant decrease in ergonomics. Those. balancing in comparison with the layout Announcer is significantly improved, but ergonomics suffered by 6.5%. The proportion of hands alternations is 75.8%.
Next, we consider the standard layout YTSUKEN , but with non-standard hands. In general, a change in the position of the hands in some measure can be considered equivalent to a change in the layout. Probably, the same can be said about the application of the dynamic method of dialing . In the non-standard hand setting, there is no amount per row as such (fingers are not located on the same row). Therefore, all keys were taken as the top row, which is higher than the main position, while the bottom row was taken as those below. The main row was taken as the main position plus the keys adjacent to its edges horizontally.
YTsUKEN staged by YVAM TOLD . The share of the middle row by pressing is 40.3%, the share of the bottom row is 13.5%. Such indicators are not very outstanding, although they are much better than in the standard formulation of the FIWA OLDJ. One can see a strong underload of the index finger of the left hand and a significant overload of the average. The share of pressing each finger of the left hand would be good if you swap the load of the middle and index fingers. On the right hand, everything is much better, except for the little finger, which produces 9.5% of the keys, which is a lot. It is obvious that the asymmetry between the hands on pressing will be the same as for the setting of the FIWA OLDJ, since the layout did not change (only the hands are changed).
A similar picture is observed in the movements of each of the fingers: the middle finger moves a lot on the left hand and the index finger moves a little. On the right - middle and nameless (middle in particular) move a little and a little - little finger (although the index finger also makes a significant proportion of movements). The asymmetry between the hands in displacement is very small - 11.58 mm to 12.21 mm (5.4%) - the best of the indicators for all the considered layouts and hand positions. The total distance for one keystroke is 23.79 mm. Those. a slight improvement compared with the production of the FIJA OLDJ.
Let us say a few words about the changes in the setting of each hand. For changing the setting of the left hand, both YVAM and YVAP are good. In comparison with FYVA, the reduction in movements on the left hand reaches 21.4%. At distances it will be about 2.5 mm cut. The TLD setting for the right hand, in comparison with the OLDJ, improves the balancing of the finger parts of the pressure, but worsens the ergonomics of the right hand by 0.8 mm (less than 5%).
The layout of YTSUKEN has one significant drawback: with any finger positioning, the right little finger is very heavily loaded. And little - ring finger.
From the point of view of the load balance of the fingers for the left hand, the setting of the UVAP is good (as well as from the point of view of ergonomics). For the right hand, the formulation of OLDJ is more ergonomic, and providing a better balance (however, also increasing the load on the little finger) - TLD. Those. the operation mode of the left hand can be seriously corrected by simply changing the setting. For the right hand, this option is not suitable. The option of changing the layout / use of dynamic dialing suggests itself.
In general, the improvement of layouts follows the path of improving the balancing of taps and movements that occur on individual fingers, along with an increase in the frequency of letters that are in the main position. For the English language, the Dvorak layouts deserve attention (according to some people, they had pains in the left wrist when switching from QWERTY to Dvorak), especially for right-handers, Colemak. For left-handers, the standard QWERTY layout will be good.
For the Russian language, it is possible to consider both a change in the main position (which improves balancing by unloading the index fingers), and alternative layouts - Announcer and Zubachev's layout. In this case, the Announcer layout corresponds more to an increase in the proportion of clicks in the main row, and the Zubachev layout improves balancing and reduces the load on the little fingers.
All of the above applies only to the classic blind set with rigid zones and standard hands, because With dynamic or recruitment, the advantages of alternative layouts will not be as significant.
QWERTY . – (27%) (39%). (.. ), . 46%/34% = 1,35. Those. 35% . . , . , , , . – 12,61 12,46 – .. . 25 . 4, .
QWERTY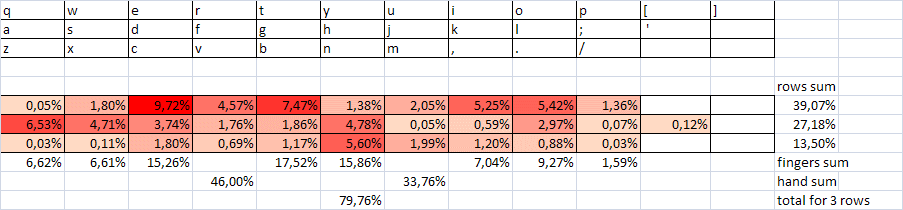

QWERTY: ; , – ; , ; ( , ) – .
Dvorak . – 55,5%. QWERTY. ( ) – 6,5%, .
Dvorak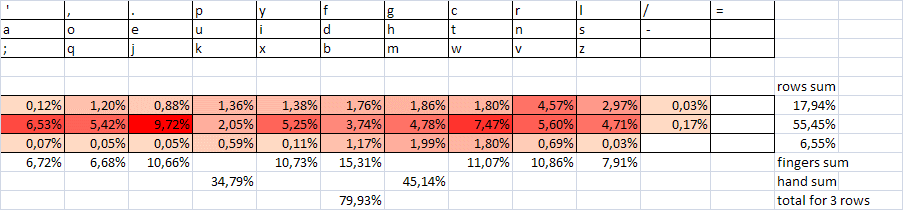

, , QWERTY. , . – , . , : 35%/45% = 0,78, , 1,28. Those. 28% . , – , . , , – 4,48 9,47 , .. , 2 . , ( ). , . 13,96 . QWERTY 80% (!). , , . , , . , , , , .
ARENSITO . , . 52,3% – . – 13,9% 13,5% – , , .. .
ARENSITO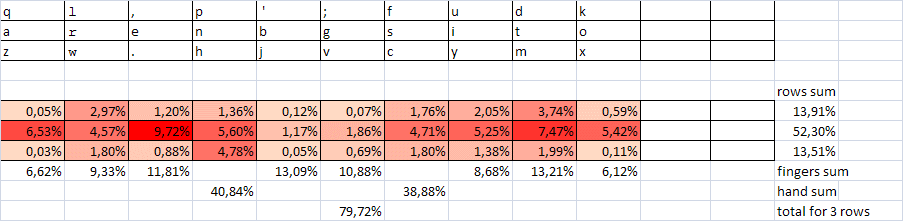

ARENSITO ( Kinesis, Maltron), . ( , Dvorak QWERTY). 13,2% (, – 10,9%), . 40,8%/38,9%=1,05, .. 5%. ( , Dvorak) – . (5,99 6,55 ) 10%- , ( ). Those. - . 12,54 – (, , , ). , Dvorak 11%. ARENSITO . . ARENSITO Dvorak.
, . QWERTY, . Dvorak, . . ARENSITO, , , ( ARENSITO), (ARENSITO ). , .
( Klausler ). 57,8% – . – 5,0% – . , , .
Klausler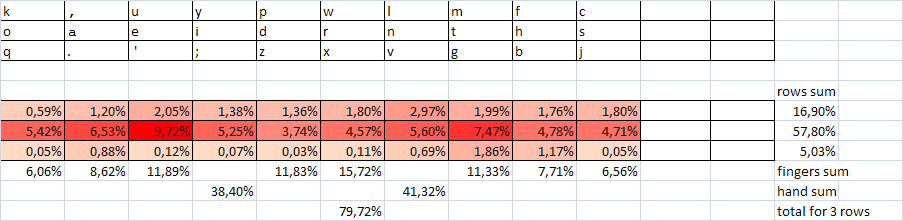

, ( ). , ARENSITO. 38,4%/41,3%=1,075 – 7,5% , . , . , . , 0,86 : , . (4,65 7,98 ), , Dvorak, - 70% . ( ) , , . , . . , Dvorak ( , , ). , , 12,56 – . , . , , Dvorak - . , .
. ( . Capewell ). . , , , . , Dvorak Klausler, , , .
51,6%. , . 10,3% – , ARENSITO, , Klausler.
Capewell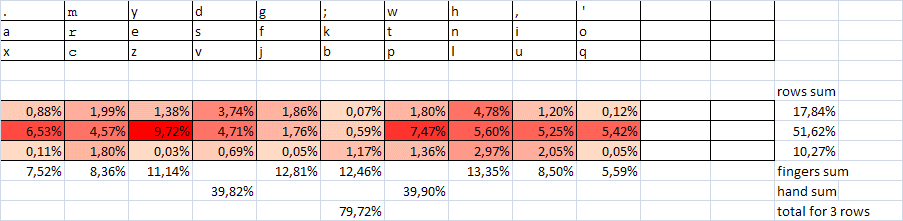

-, - (.. ), , , ARENSITO Klausler . «» – 13,4%, – 12,5%. 39,8%/39,9%=1 (!). , . , 10% ( , .. ) , , . , , . – QWERTY, .
: , – . Those. . (5,90 , 6,67 ) , 13%. 12,57 – ARENSITO (12,54 ) Klausler (12,56 ).
Colemak . , , 57,9%. ( 0,1% , Klausler, , , ; 2-3% ). – 8,5% – .
Colemak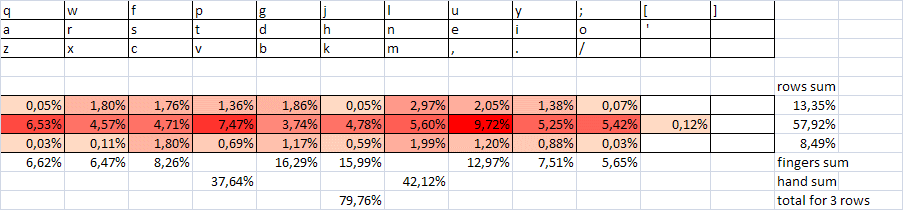

, . 16% 5,6% – . : (8,3%), -, , (6,5%) ( 0,1%). , ( , .). 37,6%/42,1%=1,12 ( 12%). – ( , , ). Those. , . (6,23 6,50 ) ( 5%). , , - , , 12,73 . .
– , (, -, , ). Those. . - . , - , , . – ARENSITO. – Capewell. – Dvorak. – Colemak.
QGMLWB . – 57,9%; – 7,8%. .
QGMLWB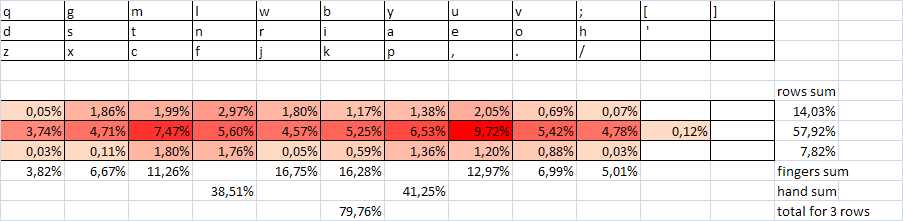

, , .. . . . . , ( QWERTY, QWERTY , ). – 38,5%/41,3% = 0,93 ( 7% ) – .
Colemak. . , Colemak – 6,96 /6,19 = 1,12. ( Colemak) . , , 13,15 , , .
, , QGMLWB, , , .
.
. 33,3%. , , .. . (26,1% 22,2%), . , , .

By interdigital balancing of the proportion of clicks, you can immediately say that the index fingers are knocked out - each of them accounts for 25% of the total number of clicks (in total, index fingers account for 50.8% of clicks, on the middle ones - 15.7%, for unnamed - 6.1%, for little fingers - 9%). For those whose index fingers are very well developed, YTsUKEN may even be a very high-speed layout (implying a set of basically two of the most powerful fingers). In general, such a layout should be quite good when working with the mouse, when only one hand rests on the keyboard. But with a blind set is made with two hands, so this plus can be very doubtful. Compared with the index heavily underloaded middle fingers, as well as unnamed. The right little finger is overloaded (even without the Shift and “-” keys). Interdigital balancing is one of the worst. The main load falls on the index. But according to the balance of the share of clicks for the hands, JTSUKEN shows a very good result: 40.6% / 41.0% (asymmetry 1%) - similar to the Capewell indicator, when compared with English-language layouts. By moving the little fingers are very heavily loaded (more than in any of the English-language layouts: they account for 3.42 mm). In other layouts, the movements of the little fingers did not have more than 1-2 mm. It can be noted that the nameless underutilized, and the index perform too much movement. The left hand gives 14.06 mm movements for one press, the right hand - 11.39 mm. Asymmetry is 23% (not a very good indicator, but far from the worst). In general, one click accounts for 25.45 mm - even more than in QWERTY, although a priori it can be assumed that, due to ergonomics, JTSUKEN should take better place among Russian-language layouts than QWERTY among English-language layouts. One of the general conclusions drawn from this point: the ergonomics of the Russian-language layouts, all other things being equal, will be worse than for English-speaking ones.
Layout Announcer . In this layout, a significant optimization has already been made in comparison with JCUKEN. The share of the main series is 52.1%. The share of the bottom row - 11.2%. When considering the share of clicks on each of the fingers, it can be seen that in comparison with YTsUKEN, the balancing of the share of clicks is significantly improved: the unnamed are loaded in accordance with their total share in much the same way as the best examples of English-language layouts. Although the right little finger is heavily loaded - 7.3% (in YTSUKEN it was 6.4%).
The distribution of the number of clicks for the layout Announcer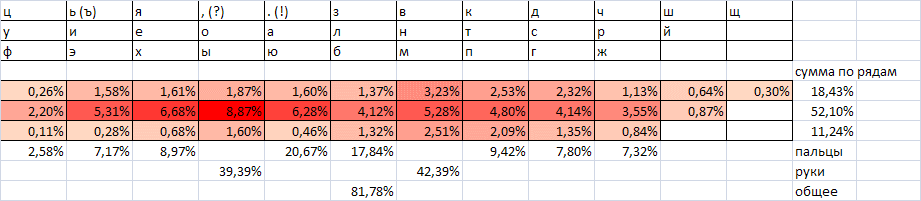

But in general, the load on the fingers of each hand decreases rather monotonously. The movements of the fingers of the left hand form a monotonously decreasing sequence, although it would be possible to load the left middle finger more heavily. For the right hand, the sequence also looks quite good, for the middle, ringless, little finger, there are approximately equal movements, with the dominance of the index finger. The right little finger passes 1.68 mm per click (this is less than in YTSUKEN, where there was 2.38 mm). The contribution to the movement of each of the hands is 6.75 mm and 10.43 mm, the asymmetry is very significant at 54%. And the general asymmetry develops, because she encourages the right hand for both pressing and moving. The average horizontal distance traveled by the fingers when you press one key is 17.18 mm, i.e. a very significant improvement over YTsUKEN (by 48%). It is also worth mentioning the frequency of the hands alternations: for YTsUKEN, it is equal to 61.2%, for the speaker’s layout - 76.2%.
The layout of D. Zubachev (links to the discussion of the layout: 1 , 2 ). The share of the main (middle) series by pressing is equal to 45.0%, the share of the lower one - 15.0%. At first glance, not very good performance. But if you look at the interdigital balance by pressing the keys, you can see very good dependencies. Besides the fact that they are monotone, these dependences have a constant change in the transition from finger to finger. And the loads of pairwise sums on the fingers of both hands (both of the index, both of the middle ones, etc.) converge with the partial loads of the fingers of each hand. Those. it can be said that the dependencies for both hands are in good agreement. At the same time, the Zubachev layout also demonstrates a rather small asymmetry of hand presses: 40.2% / 41.3% = 0.97 (asymmetry is less than 3%).
The distribution of the number of clicks for the layout Zubachev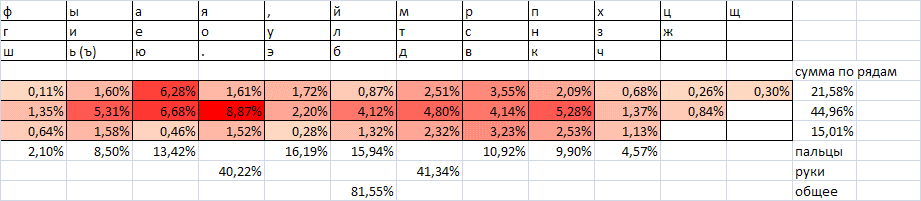

Apparently, the layout is well balanced.
The distribution of the movements on the fingers of each of the hands is subject to monotonous dependence. Finger movements are distributed fairly well, i.e. the total load on the index significantly exceeds the load on the average, etc. decreasing right up to the little fingers. The asymmetry of movement in each of the hands (7.47 mm to 10.82 mm) is 45% - less than in the Announcer, although more than in YTsUKEN. Balancing movements between hands is worse than pressing, but also not very bad (much better, for example, than for Dvorak). The average distance traveled by the fingers when you press one key is 18.30 mm and a little more than for the Speaker layout (by 6.5%). Apparently, here we come to the point that we have already encountered when considering the English-language layouts, after which an improvement in the balancing of the loads on the fingers leads to a more significant decrease in ergonomics. Those. balancing in comparison with the layout Announcer is significantly improved, but ergonomics suffered by 6.5%. The proportion of hands alternations is 75.8%.
Next, we consider the standard layout YTSUKEN , but with non-standard hands. In general, a change in the position of the hands in some measure can be considered equivalent to a change in the layout. Probably, the same can be said about the application of the dynamic method of dialing . In the non-standard hand setting, there is no amount per row as such (fingers are not located on the same row). Therefore, all keys were taken as the top row, which is higher than the main position, while the bottom row was taken as those below. The main row was taken as the main position plus the keys adjacent to its edges horizontally.
YTsUKEN staged by YVAM TOLD . The share of the middle row by pressing is 40.3%, the share of the bottom row is 13.5%. Such indicators are not very outstanding, although they are much better than in the standard formulation of the FIWA OLDJ. One can see a strong underload of the index finger of the left hand and a significant overload of the average. The share of pressing each finger of the left hand would be good if you swap the load of the middle and index fingers. On the right hand, everything is much better, except for the little finger, which produces 9.5% of the keys, which is a lot. It is obvious that the asymmetry between the hands on pressing will be the same as for the setting of the FIWA OLDJ, since the layout did not change (only the hands are changed).
A similar picture is observed in the movements of each of the fingers: the middle finger moves a lot on the left hand and the index finger moves a little. On the right - middle and nameless (middle in particular) move a little and a little - little finger (although the index finger also makes a significant proportion of movements). The asymmetry between the hands in displacement is very small - 11.58 mm to 12.21 mm (5.4%) - the best of the indicators for all the considered layouts and hand positions. The total distance for one keystroke is 23.79 mm. Those. a slight improvement compared with the production of the FIJA OLDJ.
The distribution of the number of clicks for YTsUKEN in different productions
YWAM TOLD

YVAM OLJ

YVAP OLJ
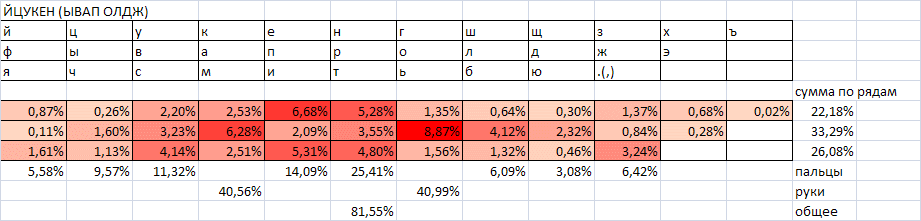

YVAM OLJ

YVAP OLJ

Let us say a few words about the changes in the setting of each hand. For changing the setting of the left hand, both YVAM and YVAP are good. In comparison with FYVA, the reduction in movements on the left hand reaches 21.4%. At distances it will be about 2.5 mm cut. The TLD setting for the right hand, in comparison with the OLDJ, improves the balancing of the finger parts of the pressure, but worsens the ergonomics of the right hand by 0.8 mm (less than 5%).
The layout of YTSUKEN has one significant drawback: with any finger positioning, the right little finger is very heavily loaded. And little - ring finger.
From the point of view of the load balance of the fingers for the left hand, the setting of the UVAP is good (as well as from the point of view of ergonomics). For the right hand, the formulation of OLDJ is more ergonomic, and providing a better balance (however, also increasing the load on the little finger) - TLD. Those. the operation mode of the left hand can be seriously corrected by simply changing the setting. For the right hand, this option is not suitable. The option of changing the layout / use of dynamic dialing suggests itself.
In general, the improvement of layouts follows the path of improving the balancing of taps and movements that occur on individual fingers, along with an increase in the frequency of letters that are in the main position. For the English language, the Dvorak layouts deserve attention (according to some people, they had pains in the left wrist when switching from QWERTY to Dvorak), especially for right-handers, Colemak. For left-handers, the standard QWERTY layout will be good.
For the Russian language, it is possible to consider both a change in the main position (which improves balancing by unloading the index fingers), and alternative layouts - Announcer and Zubachev's layout. In this case, the Announcer layout corresponds more to an increase in the proportion of clicks in the main row, and the Zubachev layout improves balancing and reduces the load on the little fingers.
All of the above applies only to the classic blind set with rigid zones and standard hands, because With dynamic or recruitment, the advantages of alternative layouts will not be as significant.
Preliminary notes on the optimization model
All or almost all the main existing models for assigning fines when optimizing layouts (such as Klausler, Capewell, QGMLWB, etc.) were analyzed. As a rule, they are not well orthogonalized. Those. one penalty component intersects with the other, taking into account the same circumstance. Example: a “jump” through a row is counted in the distance traveled by the fingers; the same jump is penalized as a difficult combination, although indirectly the same complexity is already taken into account in the distance. But twice to impose a penalty is not necessary. And there are a lot of such nuances.
After a detailed study, the model of fines on andong.azurewebsites.net turned out to be the most acceptable, but it was not finalized. On the other hand, the model http://mkweb.bcgsc.ca/carpalx/ is very well developed, but it only takes distances into account, and does not take into account the costs of keystrokes. For example, when typing characters in the main position, the penalty will be zero. While the physical work is not zero, and the speed is not infinite. The preliminary conclusion is as follows: you need to use a model, the total cost of which will be the sum of the cost of moving your finger to the desired key and the cost of pressing the key. These costs will be subject to rewards and penalties, taking into account convenient / inconvenient combinations.
Some sites, information from which was somehow useful in analyzing and comparing layouts, and was also used in building your own optimization model.
shiar.nl/misc/dvorak
dvorak.mwbrooks.com/index.html
andong.azurewebsites.net
mkweb.bcgsc.ca/carpalx
www.michaelcapewell.com/projects/keyboard/layout_capewell.htm#Capewell
www.pvv.org/~hakonhal/main.cgi/keyboard
www.maltron.com/keyboard-info/academic-papers
patorjk.com/keyboard-layout-analyzer
www.workmanlayout.com/blog
xahlee.info/kbd/dvorak_vs_colemak.html
millikeys.sourceforge.net/asset
dvorak.mwbrooks.com/index.html
andong.azurewebsites.net
mkweb.bcgsc.ca/carpalx
www.michaelcapewell.com/projects/keyboard/layout_capewell.htm#Capewell
www.pvv.org/~hakonhal/main.cgi/keyboard
www.maltron.com/keyboard-info/academic-papers
patorjk.com/keyboard-layout-analyzer
www.workmanlayout.com/blog
xahlee.info/kbd/dvorak_vs_colemak.html
millikeys.sourceforge.net/asset
Hand rotations using some non-letter keys
Let's go back a little, to the analysis of the alternations of hands.
Now, having statistics of digrams, taking into account all characters, and not just letters (NCRF), it is possible to estimate the alternation of hands and using, for example, a space. According to the frequency dictionary , the average word length in the Russian language is 5.28 characters. For each word there is one space (not counting dashes and other characters, separated by a space), i.e. roughly the frequency of the gap can be defined as 1 / (5.28 + 1) = 15.9%. To simplify further approximate calculations we will take 15%.
Diagrams with spaces account for, respectively, about 30% of all digrams, given that the space can be either at the beginning or at the end of the diagram. Then purely letter digrams will be about 70% (ignoring the other characters).
Further suppose that when typing, the “space rule” is observed: the space after the end of a word is always pressed with the other hand. In reality, of course, this rule is not fulfilled by all, and its observance does not affect somehow the speed of dialing or convenience. Rather, it is an attempt to somehow “harmonize” the set so that all fingers are loaded.
To compile a layout with spaces in mind, it is necessary to create a table that will indicate the relative frequencies of the letters representing the beginning and end of the word.
Sample table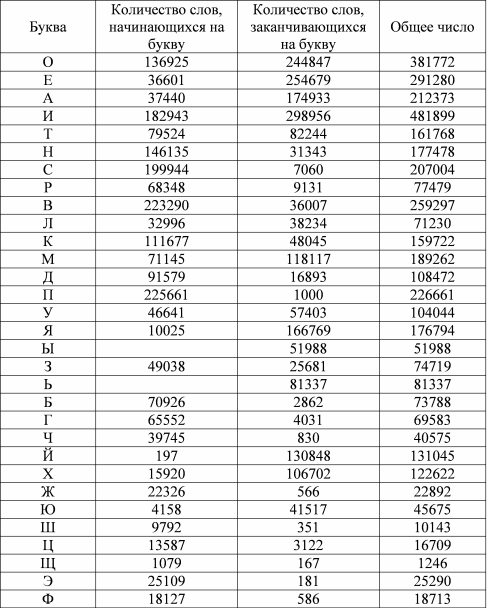

In the calculations, the total number of initial letters was normalized to correspond to the total number of final letters (this is related to the structure of the text, since all words begin with a space - follow it, but not necessarily end with it).
To take into account the alternation of hands when pressing spaces and subsequent keys, it is necessary to consider the hypothetical layout, in which such alternations occur most often, to estimate the gain. Then compare this layout with that already obtained for the criterion of the most frequent alternation of hands when typing letters, and look for a reasonable compromise between them (taking into account the maximization of the total frequency of alternations).
In this case, the maximum alternation of hands after pressing a space will be when the end of the word and the beginning of the next fall on one hand (since the space is always pressed by the opposite hand, compared to the one on which the word has ended). Mathematically, the frequency of interlaces is equivalent to the probability of such an event, and with respect to the total number of digrams, it is written:
30% * {p [lev_nach] * p [lev_kon] + p [gov_nach] * p [prav_kon]},
where p [lev_nach] is the total probability of the beginning of a word from letters on the left hand, p [lev_kon] is the total probability of the word ending on letters that fall on the same left hand; similar for the right hand.
Those. the task is to split the table into two sets of rows and maximize the sum of the products of the post-column sums of probabilities belonging to each of the sets. It sounds a bit cumbersome, but right.
In other words, we first write the same table in a probabilistic form, and then we consider the indicated post-column sums of probabilities, then the products of these sums. Thus, we obtain the probability of alternation with a space for one hand. Do the same for the other. The values obtained for both hands, add. And we strive to maximize this final amount.
Note that this aspect has mostly academic interest, since the rule of alternating spaces in most cases is not respected and the space is pressed with one hand.
Some data on the alternations attributable to alphabetic digrams and diagrams with a space
Best in hand total
by digits with spaces 21%
by letter digrams 55.8%
only 76.8%
YZUKEN
at the expense of digrams with spaces 22.2%
by letter digrams 39%
only 61.2%
Speaker
at the expense of digrams with spaces 20.2%
by letter digrams 56.1%
only 76.3%
layout D. Zubachev
due to digrams with spaces 20.6%
by letter digrams 55.2%
only 75.8%
Phonetic
at the expense of digrams with spaces 21.8%
at the expense of letter digrams 36.1%
only 57.9%
Alphabetic
at the expense of digrams with spaces 21.4%
by letter digrams 35.9%
only 57.3%
As you can see, under almost any conditions (unless specifically worsening them) alternation with a space gives an approximately constant value of 20-22%.
by digits with spaces 21%
by letter digrams 55.8%
only 76.8%
YZUKEN
at the expense of digrams with spaces 22.2%
by letter digrams 39%
only 61.2%
Speaker
at the expense of digrams with spaces 20.2%
by letter digrams 56.1%
only 76.3%
layout D. Zubachev
due to digrams with spaces 20.6%
by letter digrams 55.2%
only 75.8%
Phonetic
at the expense of digrams with spaces 21.8%
at the expense of letter digrams 36.1%
only 57.9%
Alphabetic
at the expense of digrams with spaces 21.4%
by letter digrams 35.9%
only 57.3%
As you can see, under almost any conditions (unless specifically worsening them) alternation with a space gives an approximately constant value of 20-22%.
Regarding the point and comma, we can say the following. Statistical analysis of large amounts of text (up to several hundred megabytes) shows that the comma and period are more often followed by vowels than by consonants. The same ratio is observed for interrogative and exclamation marks. Approximately 40% of the dots and commas follow after consonants, and in 60% of cases after vowels, respectively. The advantage of vowels in this case is not overwhelming, but it can be taken into account when placing the keys.
The hyphen character (dash) plays the role of a hyphen only in 30% of cases, and in 70% - is a dash, i.e. framed by spaces. After the period and comma follows in 0.1 of all cases of a hyphen, i.e. 0.1 * 30% = 3% of all uses of this symbol.
Some more interesting graphs without detailed interpretation.
Secondary data analysis site andong.azurewebsites.net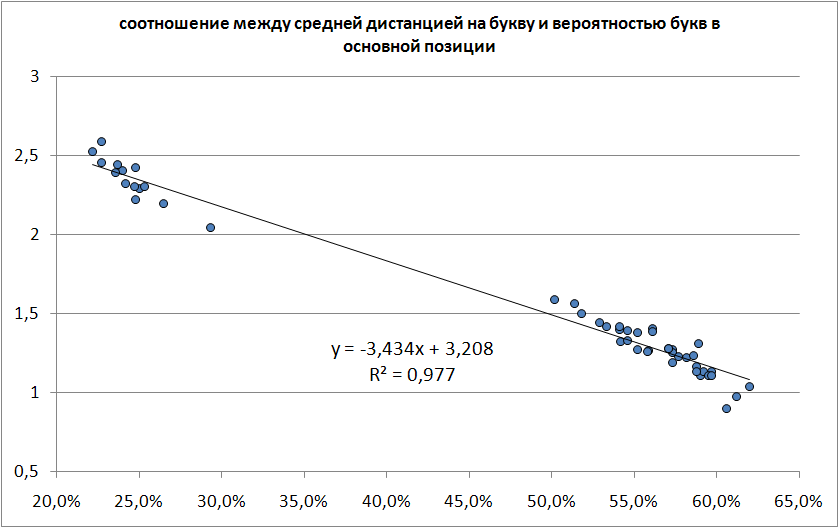
Everything is clear here - the higher the frequency of eight letters in the main position, the less the average path per click. Clear logical connection. On the left - non-optimized layouts (QWERTY, alphabetic), on the right - a family of modern, optimized (Dvorak, Maltron, Workman, Colemak.
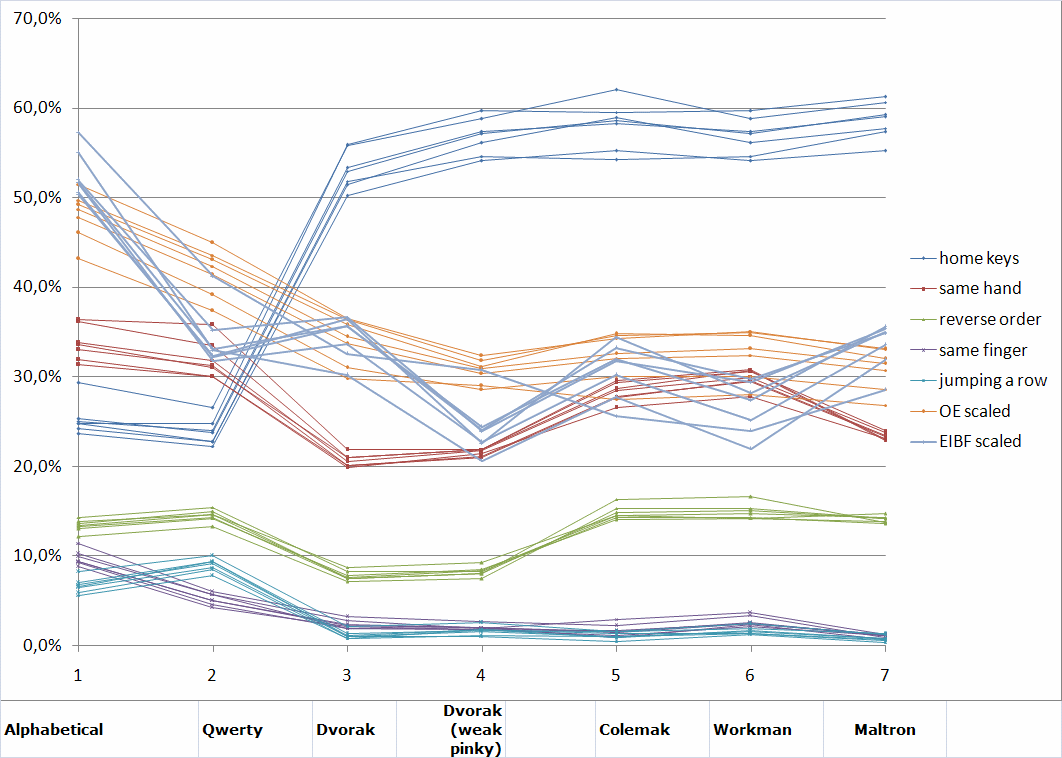
Information on various parameters of layouts. All counting algorithms from the above site. I don’t need to explain the legend, except for OE - Overall Effort - common efforts, EIBF - imbalance of loads on different fingers. It is clearly visible how two classes of layouts are distinguished by the parameters - “old” and “new”.
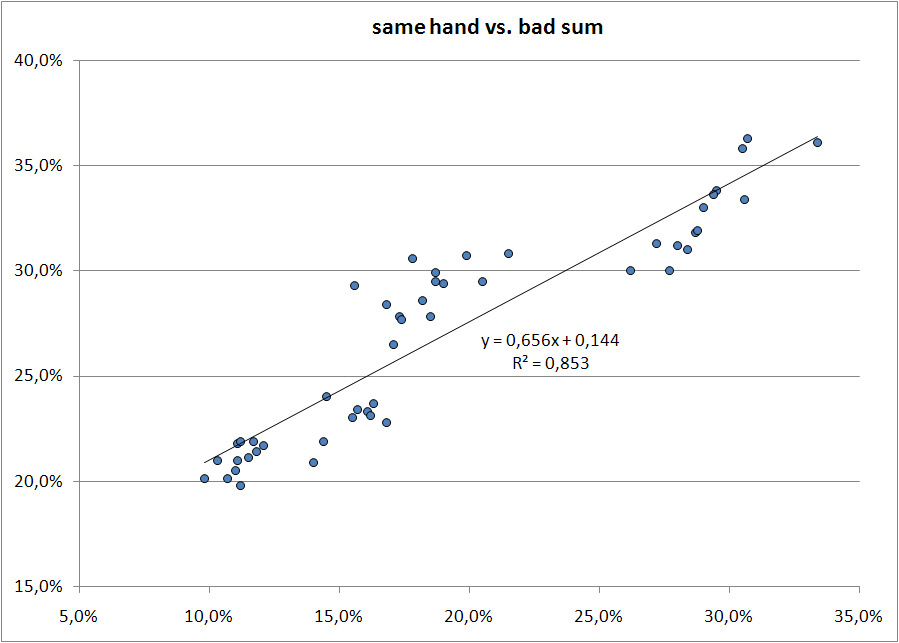
By “bad sum” is meant the sum of the probabilities of three uncomfortable combinations - “same hand”, “inverse order”, “jumping a row”. The leaders here are both Dvorak'a - standard and modified - the lower left corner of the graph.

Everything is clear here - the higher the frequency of eight letters in the main position, the less the average path per click. Clear logical connection. On the left - non-optimized layouts (QWERTY, alphabetic), on the right - a family of modern, optimized (Dvorak, Maltron, Workman, Colemak.

Information on various parameters of layouts. All counting algorithms from the above site. I don’t need to explain the legend, except for OE - Overall Effort - common efforts, EIBF - imbalance of loads on different fingers. It is clearly visible how two classes of layouts are distinguished by the parameters - “old” and “new”.

By “bad sum” is meant the sum of the probabilities of three uncomfortable combinations - “same hand”, “inverse order”, “jumping a row”. The leaders here are both Dvorak'a - standard and modified - the lower left corner of the graph.
Model building questions for layout optimization
What is the main difficulty?
Optimization methods (mathematical) are well developed, therefore, the optimization itself is not difficult. The main difficulty is to make the layout quality functional.
What will be the main criterion?
Layouts optimized for speed and comfort are generally two different things. Those.speed layout may not even be ten-finger. The same thing about convenience. But in this case, we are considering the classic method of recruitment.
What is the “blind ten-finger print method (classic) ?:
a) fixed hands;
b) fixed zones - for each finger its own letters;
c) all ten fingers are used (or nine, in case the space is pressed with one thumb).
How to make a model of quality layouts?
a) it is necessary to adequately take into account bad (good) key combinations (separately determine what is “good” or “bad”);
b) choose a compromise between convenience and speed;
c) properly distribute the load on the fingers.
In all these criteria there is some subjectivity, but there are also statements that are accepted by all as true, confirmed with the help of various programs.
For example: pressing keys with different hands, faster in speed than with one hand; set on one row more often faster than on different ones, etc.
It is necessary to collect all possible cases, analyze them, i.e. arrange in order of preference. At the same time, there should not be too many criteria.
Next you need to select the numerical quality assessment. Assume that each key combination assigns some effort in points. Less is better. Here comes subjectivism.
1st subjective choice - which key combinations are good (bad)?
2nd subjective choice - how much better (worse) is this or that combination?
There is one objective criterion - the distance traveled by the fingers from the initial position.
But here it is necessary to take into account that not only the fingers move, but also the hand, i.e. pressing each key is not necessarily from the initial position.
For example: the combination of "ST" - the brush moves to the top row, and then to the bottom. Those.the distance traveled to "T" is greater than from the starting position.
Many optimization models minimize exactly the distance, but this is not the only component, and even far from being the first in importance. The main part of the work falls not on horizontal movements of the fingers, but on keystrokes. And the number of clicks can not be reduced (without automatic replacement ).
Therefore, the main way to improve the layout - minimizing the proportion of uncomfortable combinations, taking into account the distribution of loads on the fingers of each hand.
The cost of pressing each key, according to the previous, will consist of two components: the horizontal movement and the press.
For each finger, cost coefficients for one click and unit of movement are set.
Suppose we chose the coefficients in some way. Next, you need to come up with a system of encouraging good (fast and convenient) combinations and penalizing bad ones.
Suppose we also did this. Now we have a mathematical cost model for typing.
To assess the quality of the layout for the selected model, you need to try (chase away) the layout on any text.
The sample of texts should reflect well the statistical structure of the Russian language and include:
1) a sufficient volume (from several megabytes);
2) different genres (prose, fantasy, scientific texts, journalism), since various combinations of letters and their combinations are used;
3) perhaps even different epochs (classic, modern).
Further, this text is run on the assessment quality assessment model, and the number of points is determined. The layout with the minimum (or maximum, depending on how the model is built) number of points is the best.
But testing the entire multi-megabyte text while testing various layouts is a lengthy exercise, especially since the layouts being tested are millions. Therefore, it is possible to conduct a statistical analysis of the sample and create a table of statistics of n-grams (n-character combinations, n is the desired depth of analysis). In this case, it is no longer necessary to check the entire text, but it is enough to use the statistics table, which is orders of magnitude smaller in size than the source texts. The cost of typing each combination is simply multiplied by the number of repetitions in the text of this combination.
How to choose a quasi-optimal layout, from which set? Obviously, brute force cannot do this, since the number of layouts is N = 33! = 10 64 , taking into account only the permutations of the letters.
It remains to use approximate optimization methods, they are also called heuristic search methods or random / pseudo-random optimization. The main ones I encountered in the analysis of optimization models were:
1) The basic method without any modifications - the Monte Carlo method. The layout is created randomly. We check it in accordance with the model. If it is better for the model than previously calculated, then we take it as the best and create a new layout for testing. Such a method was used by D. Zubachev in the process of searching for his layout.
The other two most commonly used methods are:
2) Imitation annealing method. Used when calculating the QGMLWB layout. Some review of this method can be found here .
3) Genetic method. Used by P. Klausler in calculating his layout. A little introduction is here .
Without further ado, it was decided to use one of the above methods, namely, the annealing method.
Note that the classical method without modifications is quite slow, it has the lowest convergence rate. Therefore, modified optimization methods are commonly used. You also need to consider that all methods of pseudo-random optimization do not guarantee finding the optimal solution, since the number of options is unimaginably large and the probability of getting exactly the best of them is negligible. Of course, in some problems where the “surface of options” has a fairly simple “relief”, you can find a global maximum / minimum, but the task of finding the optimal layout is clearly not one of those.
In the English-language articles on the topic of blind typing, there is information about how they try to take into account the fact that in the process of printing the brush moves, not the fingers. In particular, it is assumed that the neighboring finger of the hand moves in the same direction as the key that is currently pressing, but half the distance (that is, the movements are obtained as if coordinated). Interesting calculations are given in A Theory o Perfomance in skilled typing (BE John, 1996) . In it, the displacement model is supplemented by the finger positioning time, and also the times when the finger is moved up and down (key press / release) are taken into account.
The model of the printing process on three levels is very similar to reality: 1) perception, 2) cognitive, 3) motor. At low print speeds, the throughput of the process (the narrowest point) is dictated by the motor level. And at high (model speed 800 characters / min) - cognitive level. All these models come from the Model Human Processor, in which the work of the brain is modeled by a certain circuit consisting of several discrete components - handlers, buffers, etc.
Optimization Keys and Fines System
To take Shift into account when optimizing layouts, it turned out that in some cases there are not enough digram data, and the primary statistics collection algorithm needs to be modified, or it is necessary to restore the missing data, sorting through all the trigrams, etc. Digits with spaces are counted. This is also the load when recruiting. And it will affect the assessment of how profitable this or that layout. Those.spaces should lower the gain of any alternative layout, since they are pressed anyway and for all layouts the same way (if we consider the classic ten-finger dialing method).
The model was taken from the andong.azurewebsites.net site , but with various additions. The total effort (or cost) is made up of two components - pressing a key with each finger and per unit path traveled by each finger. The cost of pressing for little fingers is slightly reduced, because in the original version, they seem disproportionately high.
Costs per press:
2.10 left pinky
1.45 left unnamed
1.05 left middle
1.05 left index
1.00 right index
1.00 right average
1.40 right untitled
2.00 right little finger
1.00 big thumbs
Costs per unit of movement (the key side was taken for the unit):
1.60 left little finger
1.00 left untitled
0.55 left middle
0.75 left index
0.70 right index
0.50 right middle
0.90 right unnamed
1.50 right pinky
As we can see, the odds are somewhat larger for the left hand, which will encourage the use of the right hand in the optimization process. Those.This option is more for right-handers. For left-handers, the coefficients for the right and left hand must be changed.
We should also specify the asymmetry of hand loading. In my opinion, the asymmetry in the number of clicks is 5-10% (that is, if one hand makes 1.05-1.1 times more clicks than the other) does not matter at all.
We see that the cost of pressing taken minimal for index and middle fingers, because they are about equally developed. Perhaps the coefficients for the nameless and little finger should be further reduced.
The cost of movement is minimal for the middle finger, since it is longer than the others. A separate question about the ratio of the cost of moving for the nameless and little fingers. The little fingers are the weakest fingers, but they are more mobile, because these are extreme fingers.
For large fingers, the costs of horizontal movement are absent.
Those.for each key pressed, the costs consisted of two components: the horizontal movement and the pressing. Horizontal displacement may be zero, but total costs will never be zero (as in reality), which explains the choice of such a model as the basis.
For the presentation of a sample of texts, it was decided to use statistics digrams. On the one hand, they are much smaller than the trigrams, which should speed up the optimization process, on the other hand, even the digrams allow you to take into account the main fast / slow combinations, for example, the rotation of hands.
Additional bonuses and penalties
What additional bonuses and penalties need to be charged (i.e., how to encourage convenient, fast digrams and penalize bad ones)? It was decided to introduce the following items:
1. Speed bonus for alternating hands. Perhaps the efforts will not be less when typing a digram with different hands, but the speed on average will be much higher than when typing with one hand. We subtract 60% of the movements for the second letter of the digram (this can be justified by the fact that most of the way to the second letter will be made at the same time as pressing the first one, since in this case the hands move independently). An example of a digram is “SHU”.
2. Movement bonus for agreed motions. Here we need to remember that the fingers do not move independently, but as a whole (the TYPIST model and other works). Those.if the fingers of one hand move to the keys of the same row, then they will travel almost simultaneously. Remove 50% of the movements for the second letter of the digram. Those.in the standard layout, this would be the pressing of the letters "ShG" or "GS" or "SC" or "ES", i.e. standing on the same row (not mainly), but with different fingers.
3. Penalty for pressing the same key. Horizontal displacements for the second letter in the digram are assumed to be zero, since the finger remains above the same position. And we increase the pressure force by 20%. An example is “SS”, “EE”.
4. Penalty for the reverse combination with one hand. If the digram is typed with one hand in the direction from the center of the keyboard to the edge, then the efforts for the second letter both on movements and on pressing increase by 20% (implying a decrease in convenience and speed). An example is “YOU”, “NL”.
5. Penalty for one-finger combinations (excluding repeated pressing of the same letter). The effort to move and press increases by 30% (it is understood that the speed can be significantly reduced). Example - “MA”, “AK”, “OG”, “OT” - in the standard layout there are a lot of such combinations, since 50% of the clicks make the index fingers.
6. Penalty to jump with one hand through a row. Recalling the model of movements, we can say that if there is a jump from the top to the bottom row or vice versa, then the movements to the second letter will be larger than from the starting position. We increase the cost of moving up to the second letter by 50%. Example - "SC", "BSH", "CHU".
7. Fines bottom row. It is believed that on standard keyboards the availability of the lower row is worse than the upper one, therefore it is necessary to enter a complexity factor. For any character in the bottom row, the cost of both moving and pressing increases by 25%.
Some bonuses and penalties may act together. For example, there may be a consistent move to the bottom row, but the digram is typed in reverse order. Those.we get a bonus for the agreed movement and penalties for the bottom row and for the reverse combination with the other hand. An example is “midrange”.
This system of penalties was implemented in the MathCAD package.
Brief description of the optimization process
The initial data on digrams included all two-character combinations, determined on the basis of an analysis of 300 MB of Russian-language text provided by mystes. As mentioned, pressing Shift's is not taken into account during optimization, since this would require considerable complication, which at first glance is not justified. Accordingly, all capital letters in the statistics were converted to lowercase, and repeating digrams are grouped.
It is necessary to set the layout from which the optimization procedure will start. This layout can be any of the existing, and generated randomly. In our case, the starting layout is the YTsUKEN layout, but with one change - the hard sign and the soft sign are transferred to one key “”, and the comma is replaced by the place “b”. The comma is approximately 1.5% of all characters, and the transfer is done in order to press it without Shift.
Optimization is performed by the annealing method. The optimization step is chosen equal to one permutation of the keys. Do not choose a step too large. This can lead to the fact that the solution will not be close enough to the minimum of the objective function at all. On the other hand, a small step will reduce the rate of convergence. Practice shows that in this case one permutation of keys is a suitable step.
Annealing Optimization Graph
. . .

. . .
To obtain a reasonable result, the optimization procedure must be performed many times, and then select the best results from the results obtained. This is due to the fact that optimization is stochastic and in most cases will lead to a new result.
The number of iterations for one optimization procedure was chosen to be 1000, 5000, 10000, 50,000, 100,000. As the calculations showed, acceptable results with permissible time costs are provided by the number of iterations 10,000, if you choose from this series.
In order to assess the quality of the layout, not only a force model is used to construct a procedure that defines various characteristics, such as the
proportion of keys of the main row when typing, the
frequency of hands alternation, the
proportion of digrams recruited in reverse order,
the proportion of digrams with coordinated movements, the
proportion of digrams dialed with one finger, the
proportion of diagrams dialed not on adjacent rows with one hand.
Also determined by the breakdown of the load by clicking and moving for each finger. Based on these data, it is possible to make a more reasonable conclusion about the quality of the layout.
Proceeding from the above, optimization as a whole includes the following steps:
1. Load the source file with digram statistics, array preparation (cleaning, converting capital letters to lowercase, grouping).
2. Definition of a matrix of zones for each finger (non-standard zones can also be assigned).
3. Determination of the distance matrix for the zones of claim 2 in relative units.
4. The appointment of two matrices with penalties for moving and pressing for each finger.
5. Assignment of additional bonuses and penalties for various types of digrams.
6. The purpose of the starting layout, the choice of the optimization step, the choice of the number of iterations.
7. Optimization by the annealing method (multiple).
8. Selection of the best layouts.
9. Calculation of additional characteristics of existing Russian-language layouts and optimized layouts.
Analysis and interpretation of results
One of the best results that could be obtained from the point of view of the model described: The

data for loading the fingers in the figure and below can differ, because For optimization, several excellent initial data were used.
The upper row (not in the figure) is corrected manually - the dash is shifted to the number 8. A dash is pressed about 0.8% of all keystrokes and is far ahead of all other punctuation marks, except for the full stop and comma (for which the total is ~ 3%).
This layout provides a total cost equal to 83.5% of the cost of the layout YTSUKEN. As we see, the improvement is not very significant (16.5% by the synthetic criterion), and there is no reason to talk about any huge advantage.
The costs of other layouts with respect to the YTSUKEN layout:
YTZUKEN - 100%;
Speaker - 85.5%;
The layout of D. Zubachev - 86.8%;
Alphabetic - 111.1%.
Those.when taking into account keystrokes, and not just movements, as well as taking into account spaces, the gain becomes not so big at all, within 20%. Determining the gain purely in speed is an even more difficult task.
In one of the articles, The Standard and Dvorak Keyboards Revisited. Direct Measures of Speed (1998) , compares QWERTY and Dvorak. Dvorak is given an advantage in speed of about 4% according to a set of digrams. With the growth of skill, it can reach 10%. But in general, different authors give an advantage in Dvorak's speed from 2% to 7% for a standard skill level. So, there is nothing definite to say about speed, although the gain will obviously be even less than the gain in costs.
Let us assume that the layout, which is minimal for model costs, was obtained. And how to more objectively assess its quality? To increase objectivity, you need to apply other criteria. For example, count such commonly used indicators as hand alternation frequency, the relative number of digits dialed with one finger, the proportion of diagrams recruited in the reverse order, the proportion of digram with jump through a row, the proportion of the main row in the total number of clicks.
The following results were obtained:

Indicators:
1. The proportion of alternations of hands, due only to letter digrams;
2. The proportion of digrams with the agreed movements;
3. The proportion of digits dialed in the reverse order;
4. The proportion of digrams dialed with one finger;
5. The proportion of digrams dialed through the row;
6. The share of clicks on the main row;
7. Costs in relative units per click;
8. The path to the key in relative units (the key size is taken for the unit).
9. Costs for the left hand relative to total costs (excluding the space);
10. The cost of the right hand relative to the total cost (excluding space).
As can be seen, the optimized layout and the Zubachev layout almost coincide in the parameters, with minor variations within 1% for each of the indicators. Moreover, both results were obtained independently, according to different algorithms and according to their criteria. The layouts themselves are of course different. We can say that the optimum is somewhere very close. But which way to optimize is already subjectivism, as well as the choice of the values of fines and rewards.
In addition to the results already obtained, it was decided to search for the best permutations with the minimum number of them, by analogy with carpalx . Those.to find the first best permutation of the keys in the sense of reducing the effort, the second, etc. up to 10-15 permutations. The following results were obtained:
0. Zero permutation (manually) - combining hard and soft signs, and moving a comma to the place .
From this layout we start.
1. W / L (relative improvement relative to the previous layout of 2.8%).
2., / (-2.3%)
3. / (-1.7%)
4. / (-1.7%)
5. / (-1.6%)
6. C /. (-1.3%)
7. U / N (-1.2%)
8. U / L (-1%)
9. D / S (-0.9%)
10. H / F (-0, 5%) at this stage, the force - 1,581.
Parameters were defined for all intermediate options. It turned out that almost all the first replacements of pairs of keys lead only to an improvement in the balancing of efforts on the fingers. At the same time, the main indicators of layouts, such as alternating hands, pressing keys with one finger, etc. may even get worse. Those.The expected result, for example, that described in carpalx with the phased optimization of the English layout, could not be obtained. In this case, the first proposed replacement of E / K leads to an improvement in the alternation of hands and an increase in the frequency of the main position. In our case, the opposite is true. Almost all indicators suffered. Only starting with 5-6 permutations, these indicators begin to improve.
The calculated layout and the layout of D. Zubachev are more consistent with the optimization of the distribution of loads on the fingers. In this case, alternation suffers somewhat, to a greater extent - the frequency of the main position. The proportion of “bad” combinations also increases - backward, one-finger, jumping through a row as a result of an increase in the share of one-armed combinations.
The layout The announcer has a significantly higher proportion of the main position, and the proportion of hands alternating is also slightly higher. The proportion of bad combinations in the amount is very small. Those.The layout is very well done, but using several other criteria and at the cost of some imbalance between the fingers and the hands. For those who do not need good balancing, Announcer is the most acceptable layout.
About the issue of retraining
The study of the new layout for the same areas, as shown by our own experience, is much faster than learning the blind tenfinger method of dialing from scratch. With the experience of recruitment on YTsUKEN 4-5 years, the study of the layout Speaker up to approximately the same speed (> 500 characters / min on texts 300 characters long) occurred in 4.5 months with interruptions ( link ). Further, up to the same speed of 500 zn / min, the layout of D. Zubachev was studied, but already in 2-2.5 months ( link ).
As in all cases of learning a new skill, at the very beginning the speed of learning is the highest, then the growth rate slows down, i.e. the learning curve has an approximately logarithmic form (there is no ceiling, but for each of the next similar increments to speed, it takes several times more time / effort).
Approximate view of the learning curve

But in general, the higher the speed and the longer the experience of typing on the standard layout, the less meaningful the transition to alternative layouts is, unless the standard has very strong inconveniences.
I believe that if the speed reaches 500 characters / min and more on short sections of text, and the work experience on the standard layout is 2-3 years or more, then retraining as a whole does not make much sense. Although, there are also counterexamples , showing that even at high speeds it is possible to relearn and further increase the speed significantly. But mainly it concerns young people (15-25 years old).
In conclusion, we consider another aspect of the applicability of optimization procedures.
To the question of assessing the complexity of the text
Sometimes before the typesetters raises the question of assessing the complexity of the text. Basically, of course, this is purely competitive interest. Suppose one typesetter typed text A at a speed of 700 digits / min, and another - text B at a speed of 650 digits / min. Let the number of corrections in both cases be the same. And the length of the texts is also the same, within the limits of error.
Which of them showed the best result, given that the texts may be of different complexity?
By complexity, in this case, apparently, it is necessary to understand that texts can be composed of words of different frequency, some of which consist of worked out combinations, and others - of poorly worked. In addition, words can be of different lengths, and longer words are harder to perceive and type than standard lengths (4-6 characters). This is the first component of complexity. In the first approximation, you can simply sum up the ranks of words. The final sum (or, let's say, its logarithm) quantifies the complexity of the text.
But there is a second component, let's call it technical - how the fingers move around the keyboard, on which rows they press keys, etc. This is directly related to the layout optimization procedure already described. Only here everything will be done exactly the opposite: if in the process of optimization, different layouts were sorted out on the same language statistics, then to determine the complexity of the text, the layout will be fixed, and the input variable will be the text whose complexity needs to be evaluated.
With increasing skill of the typesetter on a specific layout, the contribution of technical complexity to the overall coefficient of complexity will fall.
Further ways to improve the model
In general, the main points when designing layouts were formulated by A. Dvorak (1936) and many other authors, including and modern (in free form):
1) Hand-drawn digrams on average are recruited faster than with one hand;
2) Digrams dialed by the neighboring fingers of one hand are slower than diagrams of fingers spread apart (except for the middle and index fingers);
3) Digrams dialed in the direction of the center-> periphery (from the index to the little finger), slower than in the direction of the periphery-> center;
4) Digrams dialed through a row are slower than diagrams on one row or on adjacent ones;
5) Digrams dialed with one finger are slower than diagrams with different fingers.
To this can add not so much.
Firstly, it is not clear in details what mathematical model was considered when optimizing the layout (meaning A. Dvorak). Which factors are more important and which are minor (although, as was shown above, the result was very good).
Secondly, it is not explicitly taken into account that the fingers belonging to one hand, when the brush is displaced, move all together (the so-called coordinated movements), although there is an echo of this in §2.4. Those.So far, there is no explicit positioning model for the brush when typing. This is a separate very complex task, which is the subject of a separate article. To solve it requires special experiments.
Thirdly, as already mentioned, the context affects the speed of printing a single character. Those.It is possible and necessary to take into account not only digrams, but also trigrams, tetragrams (3-, 4-character combinations), etc., since modern computers allow you to perform similar calculations when optimizing layouts. In general, the trigrams were already taken into account in the carpalx model , where they are divided into several categories according to convenience. But there are no references to which of them are faster and to what extent and by what means the degree of convenience / inconvenience was determined.
Fourth, at the moment there is a very powerful tool for analyzing the various parameters of typing in the face of Typing Statistics(perhaps there are analogues that are unknown to me). It should be noted that A. Dvorak, in developing his principles, also used the TS analog in the form of a paper tape, i.e. could determine the speed of a particular digram. But we must assume that the accuracy of measurement using software methods is now significantly higher.
In summary, the ways to improve the layout optimization model are still not exhausted.
And we note that now almost every student can calculate their own layout, if only they have a computer at hand. Therefore, it is not the fact of the presentation of the new layout that is of particular importance, but the features underlying the mathematical model - how this model differs from the previous ones, what new aspects of the set in it were taken into account, whether it was built on the data on the set of real typesetters, etc.
I thank Vitaly Palyanitsa for the constructive dialogue at the beginning of his work, mystes for the statistical data provided, Dmitry Zubachev for motivation, Maxim Vinokurov for several useful comments, as well as everyone who supported me in the course of my work.
Source: https://habr.com/ru/post/210826/
All Articles