Cryptanalysis hash functions GOST R 34.11-2012
At the end of 2013, the Technical Committee for Standardization "Cryptographic Information Protection" (TC 26), the Academy of Cryptography of the Russian Federation and OJSC InfoTeKS announced a contest for cryptanalysis of the national hash standard GOST R 34.11-2012. A detailed description of the conditions of the competition is published on the website www.streebog.info . Thus, we can assume that the existing work on the analysis of this cryptostandard became the subject of heightened interest of cryptanalysts, since they are the starting point for further research of the algorithm GOST R 34.11-2012.
To date, there are several works dedicated to cryptoanalysis of GOST R 34.11-2012. But it was in the work of Zongyue Wang, Hongbo Yu and Xiaoyun Wang “ Cryptanalysis of GOST R Hash Function ” that the most effective attacks on this algorithm were proposed. Therefore, in my opinion, this work is of the greatest interest among the works on this topic; its translation is what I bring to your attention.
The translation preserved the author's names of the hashing standards: under the name “GOST” I mean the 1994 standard GOST R 34.11-94, and “GOST R” refers to the GOST R 34.11-2012 algorithm studied in this paper.
The work has been translated and published in Russian with the permission of its authors.
GOST R is a standard for hash function in Russia. This paper presents some results of GOST R cryptanalysis. Using the techniques of rebound attacks, we obtained attacks that allow us to find collisions of the compression function with a reduced number of rounds. An attack on 9.5 rounds with a labor-intensive rate of 2,176 operations and memory requirements of 2,128 bytes was proposed. On the basis of this attack, a discriminator has been proposed ( Approx. Transl .: Discriminator is an algorithm that allows to distinguish the attacked function from a randomly and equally likely selected function). Moreover, a design method for k- collisions is presented for the 512-bit version of GOST R, which shows the weakness of the structure used in GOST R. As far as we know, these are the first results of the analysis of GOST R.
Keywords : hash function, GOST R, rebound attack, multicollision.
Hash functions play an important role in cryptography and are used in many applications, such as electronic signature, authentication, and data integrity. Since the MD5 and SHA-1 algorithms [1, 2] have been hacked, cryptographers have been looking for strong and efficient hash functions. The successor of the algorithm GOST, GOST R is the standard of hashing in Russia [3]. Similar in structure to Whirlpool [4], it also uses the AES-like block cipher in its compression function.
Rebound-attack is a technology using degrees of freedom, which can be used to search for collisions for hashing algorithms based on both permutations and block ciphers. This technology was first proposed in the work of Mendel (et al.) And others to form collision search attacks for the truncated Whirlpool and Grøstl algorithms [5]. It aims to effectively search for pairs of values that correspond to a predetermined truncated differential. The search procedure is divided into two phases: the internal (inbound) phase and the external (outbound) phase. In the internal phase, the attacker fully utilizes the available degrees of freedom and generates quite a few pairs of values that satisfy the paths of the truncated differential of the internal phase, used as starting points. Subsequently, in the external phase, these starting points are checked to find pairs of values that satisfy the paths of the truncated differential of the external phase.
Lamberger et al. Strengthened this technology in [6] and obtained improved results for Whirlpool. The available degrees of freedom in the key scheme are used to extend the internal phase of a rebound attack by up to two rounds. The best results of [6] are near-collision for the 9.5 round of the compression function with the complexity of 2,176 . This result was then used to construct the first distinguishing algorithm for the full 10-round compression function of the Whirlpool algorithm. At the same time, Gilbert et al. Proposed an advanced replacement technology (Super-Sbox) for a rebound attack in [7], where two rounds of AES-like transformations were considered as one level of advanced replacement. In addition, the rebound attack can also be used to analyze AES and AES-like block ciphers [8, 9], as well as ARX ciphers ( Note : ARX is an abbreviation of Add-Rotate-Xor, these operations are basic in ARX-ciphers). [ten]. Recently, using the adapted technology of rebound attacks, Duc (Duc) and others have constructed differential characteristics for Keccak in [11].
As an alternative to collision searching for hash functions, Joux proposed a method for constructing multicollisions in [12]. He showed that for an iterative hash function, the search for a multicollision is no more difficult than the search for a single collision. This method can be applied in most cases to analyze the stability of the structure of the hash function.
Due to the similarity of the GOST R and Whirlpool structure, the rebound attack used in [6] for the Whirlpool analysis can also be applied to GOST R. However, GOST P uses a matrix permutation instead of ShiftRows operation in AES-like structures. We will show that this difference leads to greater vulnerability.
In this paper, we present the first results of the GOST R analysis. More precisely, using the methods of rebound attacks, similar to those given in [6], we have received collision search attacks for 4.5, 5.5, 7.5 and 9.5 Round compression function GOST R. Our attacks on the search for collisions for the compression function GOST R are given in Table. 1. We further demonstrated that an attack on 9.5 rounds can be subsequently converted into a 10-round discriminator. In addition, we proposed a method for constructing multicollisions for the full 512-bit version of GOST R. This result shows that the structure used in GOST R is not ideal.
')
Tab. 1. Summary results for the GOST R compression function. The resource capacity indicated in brackets refers to modified attacks using a precomputed table, which requires 2,128 units of time and memory to fill.
Summary of this work: in Chapter 2, we briefly describe the GOST R hash function. Then we give a detailed description of the rebound attack in Chapter 3; A description of the discriminator will be given in Chapter 4. In Chapter 5, we will present a method for constructing multicollisions. Finally, in chapter 6 we summarize the work.
GOST R is the hash standard in Russia [3]. It processes 512-bit message blocks and calculates 512-bit or 256-bit hash values. The l- bit message is first supplemented to a size multiple of 512 bits. A single bit joins the end of the message; it is followed by 512 - 1 - ( l mod 512) zero bits. Let M = M t || M t -1 || ... || M 1 is a message consisting of t blocks after a supplement, presented in big-endian form. Then, as shown in fig. 1, the calculation of H ( M ) can be described as follows:
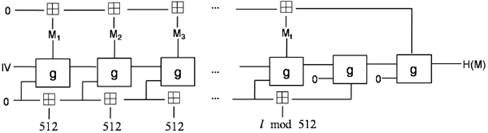
Fig. 1. Hash function GOST R
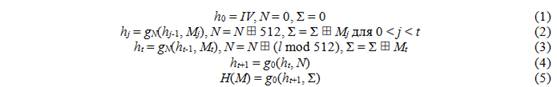
where IV is a predetermined initial value, and
denotes the operation of addition in the ring 
. g N ( h , m ) is a compression function of the GOST R algorithm, which is based on a 512-bit block cipher and is calculated as follows:
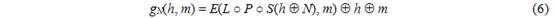
The block cipher E used in GOST R is a variant of AES, which updates the 64-byte state (represented as an 8 x 8 array - the state can also be represented as 64 x 64 in the GF (2) field) and a round key, performing 12 rounds. In each round, the state is updated by performing a round transform r i as follows:
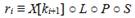
Round conversion consists of:
The round key k i is calculated as follows:
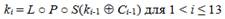
where C i - constants of the algorithm GOST R, and the initial value of k 1 is defined as
After the last round of the state update transform, the output value of the block cipher E , the previous state value h j -1, and the message block M j are combined by the XOR operation as the output value of the compression function.
We denote the result of the round transformation r i as R i +1 , and the intermediate states after the transformations S , P and L as, respectively, R i S , R i P and R i L. Initial state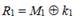
.
Rebound-attack is a hash function analysis technology that was first proposed by Mendel et al. [5] to attack Grøstl and Whirlpool with a truncated number of rounds. The main idea of this technology is to build a differential path using the available degrees of freedom to match fragments with low probability. Usually it consists of an internal phase, including a search for a match in the middle (match-in-the-middle), and a subsequent probabilistic external phase.
Using the rebound technology, we find collisions for the 4.5 and 5.5-round GOST R compression function. Moreover, using the available degrees of freedom of the key expansion scheme, as in [6], we amplify the results before the collisions for 7.5 and 9.5 rounds.
In a rebound attack, the block cipher or hash function permutation used in the compression function is divided into three parts. Let E be a block cipher, then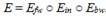
. Rebound-attack is divided into two phases:
Before describing the rebound attack on the GOST R algorithm, we briefly describe some of the properties of its linear transformation L and the table replacement of the compression function.
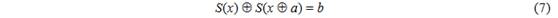
there can be only 0, 2, 4, 6, 8 and 256, which occurs with a frequency of 38235, 22454, 4377, 444, 25 and 1, respectively. On average, for a randomly selected differential ( a , b ), we can expect to find a single value as a solution. And a 256 x 256 input / output difference table can help find solutions with a little computation.
In this section, we describe the use of a rebound attack on the compression function of the GOST R algorithm, truncated to 4.5 rounds. The core of the attack is a 4-round differential path with the following sequence of active S-boxes:
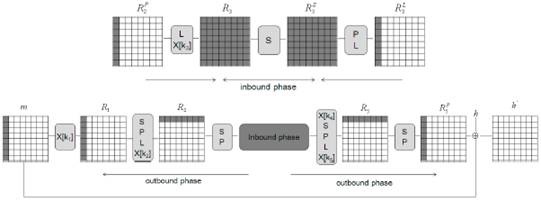
Fig. 2. Schematic representation of the attack on 4.5 rounds of the GOST R compression function. Active status bytes are highlighted in black.
In a rebound attack, we primarily divide the block cipher E into three sub-codes
. As shown in fig. 2, the most resource-intensive part of the differential path is hidden in the internal phase. Available degrees of freedom are used to maintain the differential path in E in .
In the first step of the internal phase, we start with an 8-byte difference simultaneously at the stages R 2 P and R 3 L and move forward and backward to R 3 and R 3 S, respectively (see Fig. 2). According to the propagation properties of the difference operation L , described in Section 3.2, we obtain the fully active state in both R 3 and R 3 S.
In the second step of the internal phase, we perform a search for a match at the S level in r 3 in order to find a suitable combination of input / output difference. As shown in section 3.2, we expect to find on average one solution for a given differential path. It is worth noting that there are a total of 2,128 different differential paths, and we can get no more than 2,128 actual values for R 3 and R 3 S. Since k 3 can have any value, the maximum number of start points is 2,128 + 512 = 2,640 .
In the external phase, we use the starting points developed in the internal phase and process their values in the forward and reverse directions. As shown in fig. 2, differences in R 2 P and R 3 L lead to differences only in the first columns in R 1 and R 5 P, respectively.
You can easily construct a collision for the GOST R compression function, truncated to 4.5 rounds, using the values generated in the previous step. Insofar as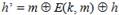
, for identical values of h and k , the same difference for m and E ( k , m ) always leads to a collision. For a pair of values generated on the external phase, the difference is equivalent for m and E ( k , m ) with a probability of 2 -64 . Therefore, we need to generate about 2 64 start points to construct collisions. The complexity of this is about 2 64 . Since we only need to store a table of 256 x 256 input / output differences for the replacement table, the memory requirements are only 2 16 bytes.
Using advanced replacement technology [7], we can enhance the 4.5 round result by adding one round to the internal phase. This leads to an attack on the 5.5-round compression function of GOST R. The external phase of this attack is the same as in the attack on 4.5 rounds, and the new sequence of active S-boxes is as follows:
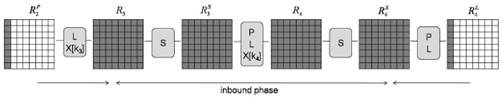
Fig. 3. The internal phase of the attack on the 5.5-round compression function GOST R
As shown in fig. 3, the values in each row of R 4 S depend only on the corresponding column of R 3 . In other words, knowing the pair of column values at stage R 3 , since we know k 4 , we can calculate the values of the corresponding row R 4 S. Consequently, we can assume that the correspondence between each column of R 3 and the corresponding row of R 4 S is an extended replacement. For each extended replacement with a randomly specified input and output difference, we expect to find an average of one real value.
Next, we describe the attack on 5.5 rounds in detail.
The internal phase of the rebound attack on 5.5 rounds of GOST R can be described as follows:
We can choose other differences in the R 2 P stage to get more valid values that satisfy the differences. For the input difference in R 2 P, we propose to find about 2 64 start points.
The outer phase is the same as in the 4.5 round attack, where we need 2 64 start points. Consequently, the complexity and memory requirements for finding a 5.5-round collision are 2 64 each .
We can improve 4.5 round results by adding 3 rounds to the internal phase by using degrees of freedom at the expense of a key expansion scheme, as in [6]. The main idea is to divide the internal phase into two subphases. These two subphases can be subsequently combined by fully using the degrees of freedom in the key expansion procedure. As a result, we get a collision for the compression function of GOST R, truncated to 7.5 rounds.
For enhanced internal phase, we use the following sequence of active bytes:
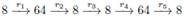
The internal phase, in turn, is divided into two subphases in order to find the input values corresponding to the differential path (Fig. 4). In the first subphase, we perform a matching search for rounds 1-2 and 4-5. And in the second subphase, we combine the active state values between r 2 and r 4 using degrees of freedom by selecting the value of the round key.
Fig. 4. The internal phase of the collision search for the 7.5-round compression function GOST R
In this subphase, we perform a matching search for rounds 1-2 and 4-5, which can be described as follows:
1. Rounds 1-2:
2. Rounds 4-5: do the same as for rounds 1-2.
Now, after performing the first subphase of the attack with a labor intensity of about 2 9 round transformations, we have 2 64 candidates for R 2 S , as well as for R 5 .
Within the framework of the second subphase, we must combine the differences in R 2 S and the differences in R 5 , as well as the actual values, using the degrees of freedom in the key expansion scheme. This means that we must solve the following equation:
at
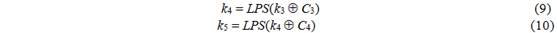
For 2 64 candidates for R 2 S and 2 64 candidates for R 5 , taking into account 512 degrees of freedom of the values of k 3 , k 4 and k 5, we expect to find 2 64 solutions. Since LP ( R 2 S ) = R 2 L and ( X [ k 5 ]) -1 = X [ k 5 ], we can rewrite (8) as follows:
Since we can always change the order of P and S and
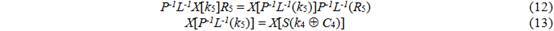
we get the following equation:
Enter the notation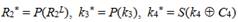
and T = P -1 L -1 ( R 5 ), then the above equation can be rewritten as:
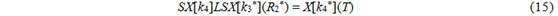
The solution of this equation is equivalent to combining the differences and the values of R 2 S and R 5 . We describe the method used to solve the equation, below.
Fig. 5. Internal subphase 2 attack by finding a collision for the 7.5-round compression function GOST R
Since the difference in R 2 L and R 4 S is fixed within subphase 1, the differences in R 2 * and T are also fixed. And 2 64 values for the states of R 2 S and R 5 generated on subphase 1, directly lead to 2 64 values for R 2 * and T, respectively. Now we can solve (15) for each row independently, as shown in fig. 5, which can be described as follows:
1. Calculate 8-byte differences and 2 64 values for R 2 * from R 2 S and calculate 8-bytes differences and corresponding 2 64 values for T from R 5 . We only need to calculate and save the string of values for R 2 * and T , since we can solve the equation line by line.The complexity and memory requirements of this step are 2 9 instead of 2 65 .
2. For all 2 64 values of the first row R 3 * repeat the following steps:
3. In this step, we combine the values of rows 2–8 for the corresponding R 2 * and T obtained in the previous step. For each row, an exhaustive search is performed independently over all 2 64 values of the corresponding key string k 3 * . Note that we want to connect 64-bit values, and by checking 2 64 key values, we expect to always find a solution.
After all these steps, we get 2 64 corresponding values, linking R 2 * and T . In other words, we get 2 64starting points for the outer phase. The complexity is about 2 128 of round transformations with the memory requirements of about 2 16 bytes. On average, we expect to find a starting point with a labor intensity of 2 64 . Step 3 can be skipped by using a 2,128 lookup table . Using the lookup table, we expect to find the starting point with an average complexity of 1. However, the complexity of building a lookup table is 2,128 , and the memory requirements are 2,128 bytes. Note that there are 2 64 differences for R 3 and 2 64 differences for R 4 S. For a fixed pair of differences in R 3 and R 4 S, we expect to find 2 64 starting points. Thus, in total, we need to generate no more than 2 192 start points for the external phase.
The outer phase of a 7.5 round attack is similar to a 4.5 round attack. The collision search attack for 7.5 rounds uses the following sequence of active bytes:
The complexity of collision search for 7.5 rounds of the GOST R compression function is about 2 64 + 64 = 2 128, with memory requirements of 2 16 bytes.
Although we can get over 2 192 start points, only 2 64 of them are required for the outer phase of the 7.5 round attack . We can expand the external phase by adding one round at the beginning and one round at the end to construct an attack to find collisions for a 9.5 round. Such an attack uses the following sequence of active bytes:
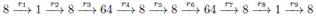
Next, we describe the external phase of the 9.5 round attack in detail.
Fig. 6. Schematic image of the attack for a 9.5-round compression function GOST R
In contrast to the external phase of the attack for 7.5 rounds, here we use truncated differentials. After the internal phase is completed, the generated values result in an 8-byte difference in R 3 and R 8 , as shown in Fig. 6. We want to match the truncated differential path 8 → 1 in both directions. The probability of this truncated differential path is 2 -56 . A 1-byte difference in R 2 and R 9 always results in 8 active bytes for R 1 and R 10 . Therefore, the probability of the external phase is 2 -112 . Therefore, we must generate in 2112 times the starting points.
Since the collision of the compression function, truncated to 9.5 rounds, requires the same difference in m and in R 10 P , we have to generate a total of 2,112 + 64 = 2,176 starting points. As described in section 3.5, we expect to find one starting point with a complexity of 2 64 . Therefore, the complexity of finding a collision for a 9.5 round is approximately 2 64 + 176 = 2 240 , and the memory requirements are 2 16 bytes. When using a lookup table with 2,128 values, the work is 2,176with memory requirements of 2,128 bytes.
In this chapter, we present the discriminator for the GOST R compression function, truncated to 10 rounds.
The type of discriminators proposed by Gilbert et al. [7] can be described as follows: for a random function that performs b -bit permutation, mapping the input difference from a subspace of size I to the output difference from a subspace of size J requires only max {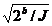
, 2 b / ( IJ )} function calls (without loss of generality, we assume that I ≤ J ).
By applying L and X [ k 11] to the previous result for the 9.5 round, we extend the differential path to 10 rounds. Even though R 11 is fully active in terms of truncated differentials, the differences in R 11 still belong to a subspace of dimension less than 64. Since the input differences of the compression function belong to a subspace of 2 64 , the output differences belong to a subspace of 2 128 . For a random function, we need 2,512- (64 + 128) = 2,320 calculations to fully determine the correspondence of the input and output differences of this kind. But for the compression function, truncated to 10 rounds, the complexity is only 2,176with memory requirements of 2 16 or 2 128 with memory requirements of 2 128 . The complexity required for the compression function is much less than that for a random function. This property can be used to distinguish the GOST-R compression function from a random function.
Now we consider the stability of the structure of the GOST R hash function. For a structure of this type, we propose a method for constructing k- collisions. In this case, the laboriousness is substantially less than the laboriousness of constructing a k- collision for an ideal structure. In other words, we prove that this kind of structure is not ideal.
For an ideal hash function with an n -bit output value, the complexity of finding a pair that gives a collision is approximately 2 n / 2 , and for searching for k- collisions (multicollisions) - 2 n ( k -1) / k. However, based on pairwise collisions, Joux on Crypto'04 [12] proposed a method of constructing 2 t- collisions for an iterative structure with a total complexity of t x 2 n / 2 . As shown in fig. 7, the attacker first generates t different pairwise collisions {( B 1 , B 1 * ), ( B 2 , B 2 * ), ..., ( B t , B t * )}. Then, the attacker can immediately get a 2 t collision of the form ( b 1 , b 2 , ..., b t ), where b i is one of the two blocks B i and B i * .
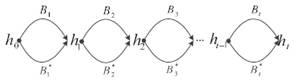
Fig. 7. Scheme 2 t- Jouay collisions. 2 t messages have the form ( b 1 , b 2 , ..., b t ), where b i is one of the two blocks B i and B i *
Despite the fact that the structure of GOST R is not iterative, for it we can also construct k- collision. This method is as follows:
1. As shown in Fig. 8, we generate 2 t messages leading to the same value of h t :
2. Among the 2 t messages generated in step 1, we are trying to find k collisions in ∑ and get k messages as a result. Note that all 2 t messages have the same N value , and these k messages always result in a k- collision hash function GOST R.
Fig. 8. Schematic representation of the construction of k collisions for GOST R.
Since all the message blocks of step 1 are of the form 0 256 || {0, 1} 256 and ∑ = b 1 b 2 ... b t , meaning bits in ∑ no more than log 2 t + 256. In the ideal model, step 2 requires 
messages to construct k collisions ∑, which requires compliance with the following inequalities, in which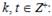 
Solving the above inequalities, we have:
176 ≤ t ≤ 2 256
and
In other words, for a t- block message, where 176 ≤ t ≤ 2 256 , we can find the k- collision of the GOST R hash function by running only calculationsThis complexity is significantly less than the complexity of finding k- collisions for the hash function of an ideal structure.
In this paper, we presented some cryptanalytic results for GOST R. At first, we described our attack on the GOST-R 4.5 compression feature using rebound attack technology. Further, this result was enhanced to 5.5 rounds using advanced replacement technology. Then the degrees of freedom of the key expansion scheme were used to achieve attacks on 7.5 rounds and 9.5 rounds. Moreover, using the result of a 9.5-round attack, we presented a 10-round discriminator for the GOST R compression function. Finally, we presented a k- collision design method for the GOST R hash function, which shows the weakness of the structure used in GOST R .
To date, there are several works dedicated to cryptoanalysis of GOST R 34.11-2012. But it was in the work of Zongyue Wang, Hongbo Yu and Xiaoyun Wang “ Cryptanalysis of GOST R Hash Function ” that the most effective attacks on this algorithm were proposed. Therefore, in my opinion, this work is of the greatest interest among the works on this topic; its translation is what I bring to your attention.
The translation preserved the author's names of the hashing standards: under the name “GOST” I mean the 1994 standard GOST R 34.11-94, and “GOST R” refers to the GOST R 34.11-2012 algorithm studied in this paper.
The work has been translated and published in Russian with the permission of its authors.
annotation
GOST R is a standard for hash function in Russia. This paper presents some results of GOST R cryptanalysis. Using the techniques of rebound attacks, we obtained attacks that allow us to find collisions of the compression function with a reduced number of rounds. An attack on 9.5 rounds with a labor-intensive rate of 2,176 operations and memory requirements of 2,128 bytes was proposed. On the basis of this attack, a discriminator has been proposed ( Approx. Transl .: Discriminator is an algorithm that allows to distinguish the attacked function from a randomly and equally likely selected function). Moreover, a design method for k- collisions is presented for the 512-bit version of GOST R, which shows the weakness of the structure used in GOST R. As far as we know, these are the first results of the analysis of GOST R.
Keywords : hash function, GOST R, rebound attack, multicollision.
1. Introduction
Hash functions play an important role in cryptography and are used in many applications, such as electronic signature, authentication, and data integrity. Since the MD5 and SHA-1 algorithms [1, 2] have been hacked, cryptographers have been looking for strong and efficient hash functions. The successor of the algorithm GOST, GOST R is the standard of hashing in Russia [3]. Similar in structure to Whirlpool [4], it also uses the AES-like block cipher in its compression function.
Rebound-attack is a technology using degrees of freedom, which can be used to search for collisions for hashing algorithms based on both permutations and block ciphers. This technology was first proposed in the work of Mendel (et al.) And others to form collision search attacks for the truncated Whirlpool and Grøstl algorithms [5]. It aims to effectively search for pairs of values that correspond to a predetermined truncated differential. The search procedure is divided into two phases: the internal (inbound) phase and the external (outbound) phase. In the internal phase, the attacker fully utilizes the available degrees of freedom and generates quite a few pairs of values that satisfy the paths of the truncated differential of the internal phase, used as starting points. Subsequently, in the external phase, these starting points are checked to find pairs of values that satisfy the paths of the truncated differential of the external phase.
Lamberger et al. Strengthened this technology in [6] and obtained improved results for Whirlpool. The available degrees of freedom in the key scheme are used to extend the internal phase of a rebound attack by up to two rounds. The best results of [6] are near-collision for the 9.5 round of the compression function with the complexity of 2,176 . This result was then used to construct the first distinguishing algorithm for the full 10-round compression function of the Whirlpool algorithm. At the same time, Gilbert et al. Proposed an advanced replacement technology (Super-Sbox) for a rebound attack in [7], where two rounds of AES-like transformations were considered as one level of advanced replacement. In addition, the rebound attack can also be used to analyze AES and AES-like block ciphers [8, 9], as well as ARX ciphers ( Note : ARX is an abbreviation of Add-Rotate-Xor, these operations are basic in ARX-ciphers). [ten]. Recently, using the adapted technology of rebound attacks, Duc (Duc) and others have constructed differential characteristics for Keccak in [11].
As an alternative to collision searching for hash functions, Joux proposed a method for constructing multicollisions in [12]. He showed that for an iterative hash function, the search for a multicollision is no more difficult than the search for a single collision. This method can be applied in most cases to analyze the stability of the structure of the hash function.
1.1. Our contribution
Due to the similarity of the GOST R and Whirlpool structure, the rebound attack used in [6] for the Whirlpool analysis can also be applied to GOST R. However, GOST P uses a matrix permutation instead of ShiftRows operation in AES-like structures. We will show that this difference leads to greater vulnerability.
In this paper, we present the first results of the GOST R analysis. More precisely, using the methods of rebound attacks, similar to those given in [6], we have received collision search attacks for 4.5, 5.5, 7.5 and 9.5 Round compression function GOST R. Our attacks on the search for collisions for the compression function GOST R are given in Table. 1. We further demonstrated that an attack on 9.5 rounds can be subsequently converted into a 10-round discriminator. In addition, we proposed a method for constructing multicollisions for the full 512-bit version of GOST R. This result shows that the structure used in GOST R is not ideal.
')
Tab. 1. Summary results for the GOST R compression function. The resource capacity indicated in brackets refers to modified attacks using a precomputed table, which requires 2,128 units of time and memory to fill.
| Rounds | Complexity / memory | Type of | Description |
| 4.5 | 2 64/2 16 | Collision | Section 3.3 |
| 5.5 | 2 64/2 64 | Collision | Section 3.4 |
| 7.5 | 2 128/2 16 | Collision | Section 3.5 |
| 9.5 | 2 240/2 16 (2 176/2 128 ) | Collision | Section 3.6 |
1.2. The content of the work
Summary of this work: in Chapter 2, we briefly describe the GOST R hash function. Then we give a detailed description of the rebound attack in Chapter 3; A description of the discriminator will be given in Chapter 4. In Chapter 5, we will present a method for constructing multicollisions. Finally, in chapter 6 we summarize the work.
2. Hash function GOST R
GOST R is the hash standard in Russia [3]. It processes 512-bit message blocks and calculates 512-bit or 256-bit hash values. The l- bit message is first supplemented to a size multiple of 512 bits. A single bit joins the end of the message; it is followed by 512 - 1 - ( l mod 512) zero bits. Let M = M t || M t -1 || ... || M 1 is a message consisting of t blocks after a supplement, presented in big-endian form. Then, as shown in fig. 1, the calculation of H ( M ) can be described as follows:
Fig. 1. Hash function GOST R
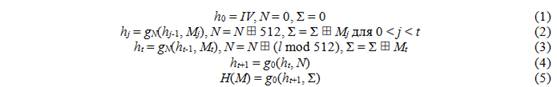
where IV is a predetermined initial value, and
denotes the operation of addition in the ring . g N ( h , m ) is a compression function of the GOST R algorithm, which is based on a 512-bit block cipher and is calculated as follows:
The block cipher E used in GOST R is a variant of AES, which updates the 64-byte state (represented as an 8 x 8 array - the state can also be represented as 64 x 64 in the GF (2) field) and a round key, performing 12 rounds. In each round, the state is updated by performing a round transform r i as follows:
Round conversion consists of:
- the level of nonlinear transformations S , where a table replacement is applied independently to each state byte;
- byte permutation P , rearranging the elements of the state matrix;
- linear transformation L , which is an independent multiplication on the right of each status line by 64 x 64 matrix A in the field GF (2);
- operations X [ k i +1 ] performing the imposition of a round key k i +1 on the state by an XOR operation.
The round key k i is calculated as follows:
where C i - constants of the algorithm GOST R, and the initial value of k 1 is defined as
After the last round of the state update transform, the output value of the block cipher E , the previous state value h j -1, and the message block M j are combined by the XOR operation as the output value of the compression function.
We denote the result of the round transformation r i as R i +1 , and the intermediate states after the transformations S , P and L as, respectively, R i S , R i P and R i L. Initial state
.
3. Rebound-attack on the compression function GOST R
Rebound-attack is a hash function analysis technology that was first proposed by Mendel et al. [5] to attack Grøstl and Whirlpool with a truncated number of rounds. The main idea of this technology is to build a differential path using the available degrees of freedom to match fragments with low probability. Usually it consists of an internal phase, including a search for a match in the middle (match-in-the-middle), and a subsequent probabilistic external phase.
Using the rebound technology, we find collisions for the 4.5 and 5.5-round GOST R compression function. Moreover, using the available degrees of freedom of the key expansion scheme, as in [6], we amplify the results before the collisions for 7.5 and 9.5 rounds.
3.1. Original rebound attack
In a rebound attack, the block cipher or hash function permutation used in the compression function is divided into three parts. Let E be a block cipher, then
. Rebound-attack is divided into two phases:
- Internal phase : this phase starts with several selected input / output differences in E in , which propagate through the linear level in the forward and reverse direction. Then all possible pairs of actual values are generated, which satisfy the required difference and correspond to the differences after one level of table replacement. These actual value pairs are starting points for the external phase.
- Outer phase : matched pairs of the inner phase are used in forward and reverse calculations via E fw and E bw to obtain the desired collisions or near-collisions. Usually E fw and E bw have a low probability, so it is necessary to repeat the internal phase to get more start points.
3.2. Preliminary calculations for rebound attacks
Before describing the rebound attack on the GOST R algorithm, we briefly describe some of the properties of its linear transformation L and the table replacement of the compression function.
- Distribution of the difference in L : since L is a linear transformation, a certain input difference in L leads to a certain output difference. Since L acts on each status line independently, the output difference of a specific line depends only on the input difference of this line. With the only active byte of the string, the L transform always results in eight active bytes, both in the forward and reverse directions, regardless of the position of the active byte.
- Differential properties S : for certain
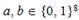the number of equality solutions
there can be only 0, 2, 4, 6, 8 and 256, which occurs with a frequency of 38235, 22454, 4377, 444, 25 and 1, respectively. On average, for a randomly selected differential ( a , b ), we can expect to find a single value as a solution. And a 256 x 256 input / output difference table can help find solutions with a little computation.
3.3. Finding collisions for the 4.5-round compression function GOST R
In this section, we describe the use of a rebound attack on the compression function of the GOST R algorithm, truncated to 4.5 rounds. The core of the attack is a 4-round differential path with the following sequence of active S-boxes:
Fig. 2. Schematic representation of the attack on 4.5 rounds of the GOST R compression function. Active status bytes are highlighted in black.
In a rebound attack, we primarily divide the block cipher E into three sub-codes
. As shown in fig. 2, the most resource-intensive part of the differential path is hidden in the internal phase. Available degrees of freedom are used to maintain the differential path in E in .
3.3.1. Internal phase
In the first step of the internal phase, we start with an 8-byte difference simultaneously at the stages R 2 P and R 3 L and move forward and backward to R 3 and R 3 S, respectively (see Fig. 2). According to the propagation properties of the difference operation L , described in Section 3.2, we obtain the fully active state in both R 3 and R 3 S.
In the second step of the internal phase, we perform a search for a match at the S level in r 3 in order to find a suitable combination of input / output difference. As shown in section 3.2, we expect to find on average one solution for a given differential path. It is worth noting that there are a total of 2,128 different differential paths, and we can get no more than 2,128 actual values for R 3 and R 3 S. Since k 3 can have any value, the maximum number of start points is 2,128 + 512 = 2,640 .
3.3.2. External phase
In the external phase, we use the starting points developed in the internal phase and process their values in the forward and reverse directions. As shown in fig. 2, differences in R 2 P and R 3 L lead to differences only in the first columns in R 1 and R 5 P, respectively.
You can easily construct a collision for the GOST R compression function, truncated to 4.5 rounds, using the values generated in the previous step. Insofar as
, for identical values of h and k , the same difference for m and E ( k , m ) always leads to a collision. For a pair of values generated on the external phase, the difference is equivalent for m and E ( k , m ) with a probability of 2 -64 . Therefore, we need to generate about 2 64 start points to construct collisions. The complexity of this is about 2 64 . Since we only need to store a table of 256 x 256 input / output differences for the replacement table, the memory requirements are only 2 16 bytes.
3.4. Finding collisions for the 5.5-round compression function GOST R
Using advanced replacement technology [7], we can enhance the 4.5 round result by adding one round to the internal phase. This leads to an attack on the 5.5-round compression function of GOST R. The external phase of this attack is the same as in the attack on 4.5 rounds, and the new sequence of active S-boxes is as follows:
Fig. 3. The internal phase of the attack on the 5.5-round compression function GOST R
As shown in fig. 3, the values in each row of R 4 S depend only on the corresponding column of R 3 . In other words, knowing the pair of column values at stage R 3 , since we know k 4 , we can calculate the values of the corresponding row R 4 S. Consequently, we can assume that the correspondence between each column of R 3 and the corresponding row of R 4 S is an extended replacement. For each extended replacement with a randomly specified input and output difference, we expect to find an average of one real value.
Next, we describe the attack on 5.5 rounds in detail.
3.4.1. Internal phase
The internal phase of the rebound attack on 5.5 rounds of GOST R can be described as follows:
- We start with a difference of 8 active bytes in the first column of R 2 P and move forward to R 3 .
- For each independent extended replacement, knowing its input difference, we process all 2 64 pairs of input values and calculate the forward replacement. This gives us 2 64 output difference values. For each difference obtained, we save the corresponding pairs of input values leading to it. This phase requires about 2 64 operations and memory.
- For each 8-byte difference in R 4 L, move back to R 4 S. We check all the previously saved values for the presence of the required difference.
We can choose other differences in the R 2 P stage to get more valid values that satisfy the differences. For the input difference in R 2 P, we propose to find about 2 64 start points.
3.4.2. External phase
The outer phase is the same as in the 4.5 round attack, where we need 2 64 start points. Consequently, the complexity and memory requirements for finding a 5.5-round collision are 2 64 each .
3.5. Finding collisions for the 7.5-round compression function GOST R
We can improve 4.5 round results by adding 3 rounds to the internal phase by using degrees of freedom at the expense of a key expansion scheme, as in [6]. The main idea is to divide the internal phase into two subphases. These two subphases can be subsequently combined by fully using the degrees of freedom in the key expansion procedure. As a result, we get a collision for the compression function of GOST R, truncated to 7.5 rounds.
For enhanced internal phase, we use the following sequence of active bytes:
The internal phase, in turn, is divided into two subphases in order to find the input values corresponding to the differential path (Fig. 4). In the first subphase, we perform a matching search for rounds 1-2 and 4-5. And in the second subphase, we combine the active state values between r 2 and r 4 using degrees of freedom by selecting the value of the round key.
Fig. 4. The internal phase of the collision search for the 7.5-round compression function GOST R
3.5.1. Internal subphase 1
In this subphase, we perform a matching search for rounds 1-2 and 4-5, which can be described as follows:
1. Rounds 1-2:
- We start with a difference of 8 bytes in the first column of R 3 and move in the opposite direction to R 2 S.
- For each difference of 8 bytes in the first column of R 1 P, we move forward to R 2 . Since there are only 2 64 different difference values in R 1 P , we can get 2 64 differences for R 2 . After matching, these differences result in approximately 2 64 valid values. However, we can perform a match search for each row independently and get 2 to 8 valid values for the row. Consequently, the laboriousness of generating 2 64 actual values corresponding to the differential path is only 2 8 round conversions.
2. Rounds 4-5: do the same as for rounds 1-2.
Now, after performing the first subphase of the attack with a labor intensity of about 2 9 round transformations, we have 2 64 candidates for R 2 S , as well as for R 5 .
3.5.2. Internal subphase 2
Within the framework of the second subphase, we must combine the differences in R 2 S and the differences in R 5 , as well as the actual values, using the degrees of freedom in the key expansion scheme. This means that we must solve the following equation:
at
For 2 64 candidates for R 2 S and 2 64 candidates for R 5 , taking into account 512 degrees of freedom of the values of k 3 , k 4 and k 5, we expect to find 2 64 solutions. Since LP ( R 2 S ) = R 2 L and ( X [ k 5 ]) -1 = X [ k 5 ], we can rewrite (8) as follows:
Since we can always change the order of P and S and
we get the following equation:
Enter the notation
and T = P -1 L -1 ( R 5 ), then the above equation can be rewritten as:
The solution of this equation is equivalent to combining the differences and the values of R 2 S and R 5 . We describe the method used to solve the equation, below.
Fig. 5. Internal subphase 2 attack by finding a collision for the 7.5-round compression function GOST R
Since the difference in R 2 L and R 4 S is fixed within subphase 1, the differences in R 2 * and T are also fixed. And 2 64 values for the states of R 2 S and R 5 generated on subphase 1, directly lead to 2 64 values for R 2 * and T, respectively. Now we can solve (15) for each row independently, as shown in fig. 5, which can be described as follows:
1. Calculate 8-byte differences and 2 64 values for R 2 * from R 2 S and calculate 8-bytes differences and corresponding 2 64 values for T from R 5 . We only need to calculate and save the string of values for R 2 * and T , since we can solve the equation line by line.The complexity and memory requirements of this step are 2 9 instead of 2 65 .
2. For all 2 64 values of the first row R 3 * repeat the following steps:
- Since the difference in R 3 * is known, for the selected value of the first row of R 3 * we calculate in the forward direction the values of the first row of R 3 L and the difference for the first row of R 4 .
- R 4 R 4 S R 4 . R 3 L , k 4 .
- k 3 * , R 2 * , R 4 S T . R 2 * , R 4 S 2 64 , . , , .
3. In this step, we combine the values of rows 2–8 for the corresponding R 2 * and T obtained in the previous step. For each row, an exhaustive search is performed independently over all 2 64 values of the corresponding key string k 3 * . Note that we want to connect 64-bit values, and by checking 2 64 key values, we expect to always find a solution.
After all these steps, we get 2 64 corresponding values, linking R 2 * and T . In other words, we get 2 64starting points for the outer phase. The complexity is about 2 128 of round transformations with the memory requirements of about 2 16 bytes. On average, we expect to find a starting point with a labor intensity of 2 64 . Step 3 can be skipped by using a 2,128 lookup table . Using the lookup table, we expect to find the starting point with an average complexity of 1. However, the complexity of building a lookup table is 2,128 , and the memory requirements are 2,128 bytes. Note that there are 2 64 differences for R 3 and 2 64 differences for R 4 S. For a fixed pair of differences in R 3 and R 4 S, we expect to find 2 64 starting points. Thus, in total, we need to generate no more than 2 192 start points for the external phase.
3.5.3. External phase
The outer phase of a 7.5 round attack is similar to a 4.5 round attack. The collision search attack for 7.5 rounds uses the following sequence of active bytes:
The complexity of collision search for 7.5 rounds of the GOST R compression function is about 2 64 + 64 = 2 128, with memory requirements of 2 16 bytes.
3.6. Finding collisions for a 9.5-round compression function GOST R
Although we can get over 2 192 start points, only 2 64 of them are required for the outer phase of the 7.5 round attack . We can expand the external phase by adding one round at the beginning and one round at the end to construct an attack to find collisions for a 9.5 round. Such an attack uses the following sequence of active bytes:
Next, we describe the external phase of the 9.5 round attack in detail.
Fig. 6. Schematic image of the attack for a 9.5-round compression function GOST R
3.6.1. External phase
In contrast to the external phase of the attack for 7.5 rounds, here we use truncated differentials. After the internal phase is completed, the generated values result in an 8-byte difference in R 3 and R 8 , as shown in Fig. 6. We want to match the truncated differential path 8 → 1 in both directions. The probability of this truncated differential path is 2 -56 . A 1-byte difference in R 2 and R 9 always results in 8 active bytes for R 1 and R 10 . Therefore, the probability of the external phase is 2 -112 . Therefore, we must generate in 2112 times the starting points.
Since the collision of the compression function, truncated to 9.5 rounds, requires the same difference in m and in R 10 P , we have to generate a total of 2,112 + 64 = 2,176 starting points. As described in section 3.5, we expect to find one starting point with a complexity of 2 64 . Therefore, the complexity of finding a collision for a 9.5 round is approximately 2 64 + 176 = 2 240 , and the memory requirements are 2 16 bytes. When using a lookup table with 2,128 values, the work is 2,176with memory requirements of 2,128 bytes.
4. Distributor for 10 rounds
In this chapter, we present the discriminator for the GOST R compression function, truncated to 10 rounds.
The type of discriminators proposed by Gilbert et al. [7] can be described as follows: for a random function that performs b -bit permutation, mapping the input difference from a subspace of size I to the output difference from a subspace of size J requires only max {
, 2 b / ( IJ )} function calls (without loss of generality, we assume that I ≤ J ).
By applying L and X [ k 11] to the previous result for the 9.5 round, we extend the differential path to 10 rounds. Even though R 11 is fully active in terms of truncated differentials, the differences in R 11 still belong to a subspace of dimension less than 64. Since the input differences of the compression function belong to a subspace of 2 64 , the output differences belong to a subspace of 2 128 . For a random function, we need 2,512- (64 + 128) = 2,320 calculations to fully determine the correspondence of the input and output differences of this kind. But for the compression function, truncated to 10 rounds, the complexity is only 2,176with memory requirements of 2 16 or 2 128 with memory requirements of 2 128 . The complexity required for the compression function is much less than that for a random function. This property can be used to distinguish the GOST-R compression function from a random function.
5. Multicollision hash function GOST R
Now we consider the stability of the structure of the GOST R hash function. For a structure of this type, we propose a method for constructing k- collisions. In this case, the laboriousness is substantially less than the laboriousness of constructing a k- collision for an ideal structure. In other words, we prove that this kind of structure is not ideal.
For an ideal hash function with an n -bit output value, the complexity of finding a pair that gives a collision is approximately 2 n / 2 , and for searching for k- collisions (multicollisions) - 2 n ( k -1) / k. However, based on pairwise collisions, Joux on Crypto'04 [12] proposed a method of constructing 2 t- collisions for an iterative structure with a total complexity of t x 2 n / 2 . As shown in fig. 7, the attacker first generates t different pairwise collisions {( B 1 , B 1 * ), ( B 2 , B 2 * ), ..., ( B t , B t * )}. Then, the attacker can immediately get a 2 t collision of the form ( b 1 , b 2 , ..., b t ), where b i is one of the two blocks B i and B i * .
Fig. 7. Scheme 2 t- Jouay collisions. 2 t messages have the form ( b 1 , b 2 , ..., b t ), where b i is one of the two blocks B i and B i *
Despite the fact that the structure of GOST R is not iterative, for it we can also construct k- collision. This method is as follows:
1. As shown in Fig. 8, we generate 2 t messages leading to the same value of h t :
- Let h 0 be the initial value of the IV algorithm GOST R.
- i 1 t :
- B i B i * , g N ( h i -1 , B i ) = g N ( h i -1 , B i *), B i B i * 0 256 || {0, 1} 256 . 2 256 , [13].
- Compiling the resulting 2 t messages in the form ( b 1 , ..., b t ), where b i is one of two blocks: B i or B i * .
2. Among the 2 t messages generated in step 1, we are trying to find k collisions in ∑ and get k messages as a result. Note that all 2 t messages have the same N value , and these k messages always result in a k- collision hash function GOST R.
Fig. 8. Schematic representation of the construction of k collisions for GOST R.
Since all the message blocks of step 1 are of the form 0 256 || {0, 1} 256 and ∑ = b 1
b 2 ... b t , meaning bits in ∑ no more than log 2 t + 256. In the ideal model, step 2 requires messages to construct k collisions ∑, which requires compliance with the following inequalities, in which
Solving the above inequalities, we have:
176 ≤ t ≤ 2 256
and
In other words, for a t- block message, where 176 ≤ t ≤ 2 256 , we can find the k- collision of the GOST R hash function by running only
calculationsThis complexity is significantly less than the complexity of finding k- collisions for the hash function of an ideal structure.
6. Conclusion
In this paper, we presented some cryptanalytic results for GOST R. At first, we described our attack on the GOST-R 4.5 compression feature using rebound attack technology. Further, this result was enhanced to 5.5 rounds using advanced replacement technology. Then the degrees of freedom of the key expansion scheme were used to achieve attacks on 7.5 rounds and 9.5 rounds. Moreover, using the result of a 9.5-round attack, we presented a 10-round discriminator for the GOST R compression function. Finally, we presented a k- collision design method for the GOST R hash function, which shows the weakness of the structure used in GOST R .
Literature
- X. Wang, H. Yu. How to Break MD5 and Other Hash Functions, in: Advances in Cryptology – EUROCRYPT 2005, Springer, 2005, pp. 19–35.
- X. Wang, YL Yin, H. Yu, Finding Collisions in the Full SHA-1, in: Advances in Cryptology–CRYPTO 2005, Springer, 2005, pp. 17–36.
- V. Dolmatov, Gost R 34.11-94: Hash function algorithm.
- P. Barreto, V. Rijmen, The Whirlpool Hashing Function, in: First open NESSIE Workshop, Leuven, Belgium, Vol. 13, 2000, p. 14.
- F. Mendel, C. Rechberger, M. Schläffer, SS Thomsen, The Rebound Attack: Cryptanalysis of Reduced Whirlpool and Grøstl, in: Fast Software Encryption, Springer, 2009, pp. 260–276.
- M. Lamberger, F. Mendel, C. Rechberger, V. Rijmen, M. Schläffer, Rebound Distinguishers: Results on the Full Whirlpool Compression Function, in: Advances in Cryptology–ASIACRYPT 2009, Springer, 2009, pp. 126–143.
- H. Gilbert, T. Peyrin, Super-sbox Cryptanalysis: Improved Attacks for AES-like Permutations, in: Fast Software Encryption, Springer, 2010, pp. 365–383.
- O. Dunkelman, N. Keller, A. Shamir, Improved Single-Key Attacks on 8-Round AES-192 and AES-256, in: Advances in Cryptology-ASIACRYPT 2010, Springer, 2010, pp. 158–176.
- F. Mendel, T. Peyrin, C. Rechberger, M. Schläffer, Improved Cryptanalysis of the Reduced Grøstl Compression Function, Echo Permutation and AES Block Cipher, in: Selected Areas in Cryptography, Springer, 2009, pp. 16–35.
- D. Khovratovich, I. Nikolić, C. Rechberger, Rotational Rebound Attacks on Reduced Skein, in: Advances in Cryptology-ASIACRYPT 2010, Springer, 2010, pp. 1–19.
- A. Duc, J. Guo, T. Peyrin, L. Wei, Unaligned Rebound Attack: Application to Keccak, in: Fast Software Encryption, Springer, 2012, pp. 402–421.
- A. Joux, Multicollisions in Iterated Hash Functions: Application to Cascaded Constructions, in: Advances in Cryptology–CRYPTO 2004, Springer, 2004, pp. 306–316.
- D. Wagner, A Generalized Birthday Problem, in: Advances in Cryptology–CRYPTO 2002, Springer, 2002, pp. 288–304.
Source: https://habr.com/ru/post/210684/
All Articles