Spatio-temporal image processing on GPU
Not so long ago it became popular to use video cards for computing. One fine day, a few years ago, and I looked at a new, then, CUDA technology. There was a good card in the hands of those times GTX8800, and there were also tasks for parallelization.
Who worked with the GPU, knows about the integration of requests, the conflict of banks and how to deal with it, and if it did not work, then you can find several useful articles on the basics of programming on CUDA [1] . The GTX8800 card, in a sense, was good because it was one of the first and supported only the first versions of CUDA, so it was clearly visible on it when there are bank conflicts or global memory requests are not merged, because time increased in this case times. All this helped to better understand all the rules for working with the map and write normal code.
In new models add more and more functionality, which facilitates and accelerates the development. Atomic operations, cache, dynamic parallelism, etc. appeared.
In the post, I will tell you about the space-time filtering of images and the implementation for compute capability = 1.0, and how you can accelerate the resulting result with new features.
Temporal filtering can be useful when observing satellites or in other filtering situations when precise background suppression is required.

Cut as far as I could, but left the most important thing. So, at the entrance comes a sequence of frames. Each frame can be represented as the sum of the matrix noise, the background and the useful signal.
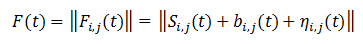
Using several previous frames, you can whitewash the newly arrived frame and highlight the signal, if present. To do this, it is necessary to predict the background on this frame, to get its assessment, according to the implementation in the previous frames. Let the number of frames in the history of N, then the background estimate can be represented as the sum of frames with some weights.
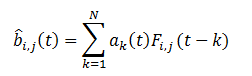
The quality criterion will be the difference of the frame and the predicted background, which must be minimized.
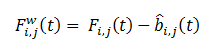
The solution is:
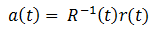
The sample correlation matrix is calculated as:
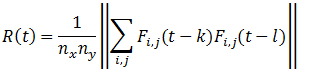
and the vector of the right side has the form:
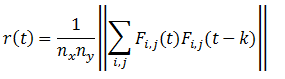
where k, l - vary from 1 to N.
However, this method does not take into account frame shift. If we present the coefficients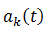 as an explicit shift function
as an explicit shift function 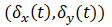 relative to some reference frame, it is possible to formulate a quality criterion and write a solution. There should be a lot of formulas, but as a result
relative to some reference frame, it is possible to formulate a quality criterion and write a solution. There should be a lot of formulas, but as a result 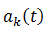 depends only on shifts.
depends only on shifts.
Shifts are calculated relative to some reference frame. according to the following formulas:
according to the following formulas:
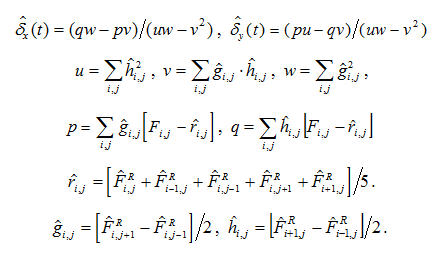
Knowing the frame shifts relative to the reference frame, we calculate the vector of coefficients a (t) using the following formula:
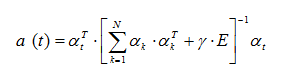
Where α is a vector of coefficients of a polynomial of degree n, γ is a sufficiently small quantity, E is the identity matrix.
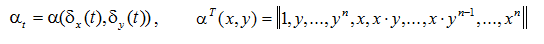
Consider the implementation of the second filtering method. On the GPU, it is beneficial to transfer the frame whitening function and the function of finding frame shifts. The function of calculating the whitening coefficients by known shifts takes little time and is too small in size.
Immediately, I’ll make a reservation that this is one of the first projects I wrote, so the code does not pretend to perfection, however, I will try to point out the flaws and ways to correct them, some of them we will fix and look at the result.
First, in the memory of the video card you need to throw a sequence of frames. To do this, select an array with pointers to the GPU memory and then copy it into the GPU memory too.
')
With such an organization there is a small flaw. If you read from the frame as follows
then in earlier versions of the compute capability, with such a reading, requests were not merged into global memory.
This is now a cache and pointers to frames are deposited in it and quickly read. To satisfy the rules for merging requests, you must either preload these pointers into shared memory (which also takes time) or, for example, do this:
In this case, the read request will be merged and we will notice a noticeable speed increase.
The frame whitening function for a GPU looks like this:
In general, everything is simple, we create shared memory for the result of the whitening of the frame, load our vector of coefficients, synchronize the threads, and further in the cycle we whitewash our frame with these coefficients. Also here you can choose not a square block of flows, but a linear one, which in general will be even more correct, since it will reduce the number of calculations in the indexing.
For the shift search function, a standard optimized algorithm was used to search for the sum of the array [2] . In this function, you must first find the coefficients rij, gij, hij and then calculate it using the sum formulas given above.
At the very end, it is still necessary to add the results for all the blocks. Since the number of blocks is not very large, the result is more profitable to get on the processor. Since for each frame the shift is calculated independently, we can come up with an implementation when one core counts the shift for all frames, adding another dimension to the flow table for indexing the filter memory frames. However, it will be beneficial if the frames are small.
What are the main disadvantages here.
1. The final result we get on the processor.
2. The coefficients for the reference frame rij, gij, hij are repeatedly calculated for each frame.
Let's look at the result in the profiler and evaluate whether this implementation works well. The profiler tells us that the read requests are merged, and the instructions take up most of the time.
Offset Search Core:

Core to whitewash staff:

Since the old GTX8800 was on a different computer and had already gone somewhere, I’m bringing results for the GTX Titan.
For frames of size 512x512, the following work time results were obtained. The core for calculating the shift coefficients takes 60 μs. If we add to it the copying of the coefficients and the final summation, we get 130 μs. With a memory of 20 frames, the running time is 2.6 ms, respectively. The whitening function takes 156 µs. There is also a function for calculating the coefficients on the processor; this is another 50 µs. The total is 2.806 ms.
Accordingly, on the CPU, the calculation of shifts takes 40 ms, the whitening of the frame is 30 ms and the calculation of the coefficients is another 50 μs. In total, it turns out 70 ms, which is 25 times slower than on the GPU (in fact, it is not, but more on that later).
The implementation is quite simple and is compatible with SS = 1.0. Let's now see what can be fixed. The last action in the search for shifts can be changed and implemented through atomic operations, which will work several times faster.
The modified code now looks like this:
In this case, the core takes about the same time, 66 µs.
You can get rid of multiple recounting rij, gij, hij by writing a separate kernel to calculate them, but then you have to load them every time, and this is three times more memory, since instead of loading one reference frame you will have to load three frames with coefficients. The optimal solution would be to make one core to calculate all the shifts at once, making a frame-by-frame loop inside the core.
Suppose that we have a more general task and could not have done so, and it would have been necessary to launch the kernel many times. At this point, you might think that everything is fine, the cores are written as a whole optimally, and the acceleration turned out up to 25 times, but if you look at the profiler, we will see the following picture:

Our functions on the GPU work only a small amount of time, the rest is delays, copying memory and other intermediate operations. In total, it raises 11.5 ms to calculate the offsets for all frames. As a result, the acceleration turned out only 6 times relative to the CPU. Remove all intermediate calculations and run the kernels one after the other in a loop:
After optimization, the profiler shows a completely different picture.

Much nicer turned out, really? .. Now the part with the calculation of shifts takes 1.40 ms instead of 11.5 ms. There remained a small interval between the cores of 4 µs, which is given by the profiler. And now let's try to run the kernel in different threads.
Now the profiler shows this result and here the interval is 1.22 ms.

And it is even less by 0.12 ms than 0.066 * 20 = 1.320.
The processor load is 84%.

As a result, the total time is 1.22 ms + 50 μs + 156 μs = 1.426 ms, which is 50 times faster than on the CPU.
Of course, it would be more correct to write one core for calculating shifts, but this is another way of optimization, and we considered a more general way, which cannot be underestimated. You can write a good implementation on the GPU, but forget about optimizing interaction with the GPU. The less time it takes for the kernel to work, the more the intervals between calls in which there are any actions on the CPU will be affected.
For example, images of the starry sky were taken, a moving dim object was added to them, small vibrations and self-noise.
Before processing:

After treatment:

Before processing:

After treatment:

In addition to the algorithm, it is possible and even necessary to add the function of deleting an object from previous frames, since it can badly spoil the result of filtering, leaving traces behind.
Unfortunately, the real recording did not work out, but if it works out and it will be interesting for readers, I will write about the results.
PS Found 4GB 10Mpix frames with a wide-angle camera. I'll try to process.
1. Work with memory in CUDA.
2. The algorithm for calculating the amount of CUDA.
Who worked with the GPU, knows about the integration of requests, the conflict of banks and how to deal with it, and if it did not work, then you can find several useful articles on the basics of programming on CUDA [1] . The GTX8800 card, in a sense, was good because it was one of the first and supported only the first versions of CUDA, so it was clearly visible on it when there are bank conflicts or global memory requests are not merged, because time increased in this case times. All this helped to better understand all the rules for working with the map and write normal code.
In new models add more and more functionality, which facilitates and accelerates the development. Atomic operations, cache, dynamic parallelism, etc. appeared.
In the post, I will tell you about the space-time filtering of images and the implementation for compute capability = 1.0, and how you can accelerate the resulting result with new features.
Temporal filtering can be useful when observing satellites or in other filtering situations when precise background suppression is required.

Some theory
Cut as far as I could, but left the most important thing. So, at the entrance comes a sequence of frames. Each frame can be represented as the sum of the matrix noise, the background and the useful signal.
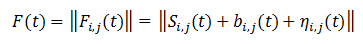
Using several previous frames, you can whitewash the newly arrived frame and highlight the signal, if present. To do this, it is necessary to predict the background on this frame, to get its assessment, according to the implementation in the previous frames. Let the number of frames in the history of N, then the background estimate can be represented as the sum of frames with some weights.
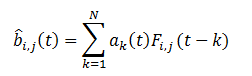
The quality criterion will be the difference of the frame and the predicted background, which must be minimized.
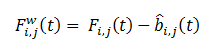
The solution is:
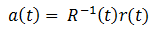
The sample correlation matrix is calculated as:
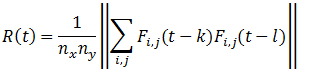
and the vector of the right side has the form:
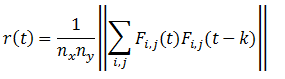
where k, l - vary from 1 to N.
However, this method does not take into account frame shift. If we present the coefficients
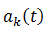 as an explicit shift function
as an explicit shift function 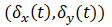 relative to some reference frame, it is possible to formulate a quality criterion and write a solution. There should be a lot of formulas, but as a result
relative to some reference frame, it is possible to formulate a quality criterion and write a solution. There should be a lot of formulas, but as a result 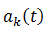 depends only on shifts.
depends only on shifts.Shifts are calculated relative to some reference frame.
 according to the following formulas:
according to the following formulas: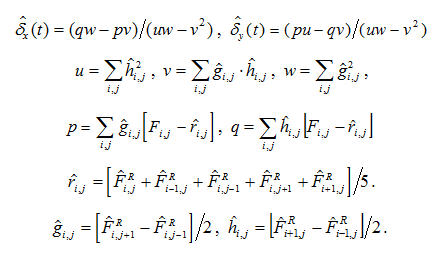
Knowing the frame shifts relative to the reference frame, we calculate the vector of coefficients a (t) using the following formula:
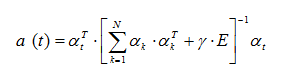
Where α is a vector of coefficients of a polynomial of degree n, γ is a sufficiently small quantity, E is the identity matrix.
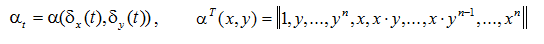
GPU implementation
Consider the implementation of the second filtering method. On the GPU, it is beneficial to transfer the frame whitening function and the function of finding frame shifts. The function of calculating the whitening coefficients by known shifts takes little time and is too small in size.
Immediately, I’ll make a reservation that this is one of the first projects I wrote, so the code does not pretend to perfection, however, I will try to point out the flaws and ways to correct them, some of them we will fix and look at the result.
First, in the memory of the video card you need to throw a sequence of frames. To do this, select an array with pointers to the GPU memory and then copy it into the GPU memory too.
float **h_array_list, **d_array_list; h_array_list = ( float** )malloc( num_arrays * sizeof( float* )); cudaMalloc((void**)&d_array_list, num_arrays * sizeof( float * )); for ( int i = 0; i < num_arrays; i++ ) cudaMalloc((void**)&h_array_list[i], data_size); cudaMemcpy( d_array_list, h_array_list, num_arrays * sizeof(float*), cudaMemcpyHostToDevice ); ')
With such an organization there is a small flaw. If you read from the frame as follows
int bx = blockIdx.x; int by = blockIdx.y; int tx = threadIdx.x; int ty = threadIdx.y; int aBegin = nx * BLOCK_SIZE * by + BLOCK_SIZE * bx; float a = inFrame[ j ][ aBegin + nx * ty + tx] then in earlier versions of the compute capability, with such a reading, requests were not merged into global memory.
This is now a cache and pointers to frames are deposited in it and quickly read. To satisfy the rules for merging requests, you must either preload these pointers into shared memory (which also takes time) or, for example, do this:
float **h_array_list, **d_array_list; h_array_list = ( float** )malloc( 16 * num_arrays * sizeof( float* ) ); cudaMalloc((void**)&d_array_list, 16 * num_arrays * sizeof(float *)); for ( int i = 0; i < num_arrays; i++ ) { cudaMalloc((void**)&h_array_list[i*16], data_size); for( int j = 1; j < 16; j++ ) h_array_list[ i*16 + j ] = h_array_list[ i*16 ]; } cudaMemcpy( d_array_list, h_array_list, 16*num_arrays * sizeof(float*), cudaMemcpyHostToDevice ); In this case, the read request will be merged and we will notice a noticeable speed increase.
The frame whitening function for a GPU looks like this:
__global__ void kernelWhite( float * out, float ** inFrame, float *at, int nx, int mem ) { int bx = blockIdx.x; int by = blockIdx.y; int tx = threadIdx.x; int ty = threadIdx.y; int aBegin = nx * BLOCK_SIZE * by + BLOCK_SIZE * bx; __shared__ float frame1 [BLOCK_SIZE][BLOCK_SIZE]; __shared__ float a [32]; int i = ty * BLOCK_SIZE + tx; // if( i < mem ) a[ i ] = at[ i ]; __syncthreads (); frame1 [ty][tx] = 0; // for( int j = 0; j < mem; j++ ) { frame1 [ty][tx] += a[ j ]*inFrame[ j*16 + tx ][ aBegin + nx * ty + tx]; } // out [ aBegin + nx * ty + tx ] = inFrame[ mem*16 + tx ][ aBegin + nx * ty + tx] - frame1 [ty][tx]; } In general, everything is simple, we create shared memory for the result of the whitening of the frame, load our vector of coefficients, synchronize the threads, and further in the cycle we whitewash our frame with these coefficients. Also here you can choose not a square block of flows, but a linear one, which in general will be even more correct, since it will reduce the number of calculations in the indexing.
For the shift search function, a standard optimized algorithm was used to search for the sum of the array [2] . In this function, you must first find the coefficients rij, gij, hij and then calculate it using the sum formulas given above.
__global__ void kernelShift (float * inFrameR, float * inFrame, float * outData, int nx)
__global__ void kernelShift ( float *inFrameR, float *inFrame, float *outData, int nx ) { int bx = blockIdx.x; int by = blockIdx.y; int tx = threadIdx.x; int ty = threadIdx.y; int aBegin = nx * BLOCK_SIZE * by + BLOCK_SIZE * bx; // __shared__ float rij [BLOCK_SIZE*BLOCK_SIZE]; __shared__ float gij [BLOCK_SIZE*BLOCK_SIZE]; __shared__ float hij [BLOCK_SIZE*BLOCK_SIZE]; __shared__ float tmp [BLOCK_SIZE*BLOCK_SIZE]; __shared__ float p [BLOCK_SIZE*BLOCK_SIZE]; __shared__ float q [BLOCK_SIZE*BLOCK_SIZE]; __shared__ float frame1 [BLOCK_SIZE][BLOCK_SIZE]; // shared memeory frame1 [ty][tx] = inFrameR [ aBegin + nx * ty + tx]; // __syncthreads (); int i = ty * BLOCK_SIZE + tx; // gij, hij, rij 1414. if( tx > 0 && > 0 && tx < BLOCK_SIZEm1 && ty < BLOCK_SIZEm1 ) { gij[ i ] = ( frame1[ty + 1][tx] - frame1[ty - 1][tx] )/2.0; hij[ i ] = ( frame1[ty][tx + 1] - frame1[ty][tx - 1] )/2.0; rij[ i ] = ( frame1[ty][tx] + frame1[ty][tx + 1] + frame1[ty][tx - 1] + frame1[ty + 1][tx] + frame1[ty - 1][tx] )/5.0; } else { gij[ i ] = 0; hij[ i ] = 0; rij[ i ] = 0; } // __syncthreads (); // shared memeory frame1 [ty][tx] = inFrame [ aBegin + nx * ty + tx] - rij[i]; // p, q p [i] = gij [i]*frame1 [ty][tx]; q [i] = hij [i]*frame1 [ty][tx]; // u tmp [i] = hij [i]*hij [i]; // v rij[i] = hij [i]*gij [i]; // w hij [i] = gij [i]*gij [i]; __syncthreads (); for ( int s = BLOCK_SIZEhalfqrt; s > 32; s >>= 1 ) { if ( i < s ) { p [i] += p [i + s]; q [i] += q [i + s]; tmp [i] += tmp [i + s]; rij [i] += rij [i + s]; hij [i] += hij [i + s]; } __syncthreads (); } if ( i < 32 ) { p [i] += p [i + 32]; p [i] += p [i + 16]; p [i] += p [i + 8]; p [i] += p [i + 4]; p [i] += p [i + 2]; p [i] += p [i + 1]; q [i] += q [i + 32]; q [i] += q [i + 16]; q [i] += q [i + 8]; q [i] += q [i + 4]; q [i] += q [i + 2]; q [i] += q [i + 1]; tmp [i] += tmp [i + 32]; tmp [i] += tmp [i + 16]; tmp [i] += tmp [i + 8]; tmp [i] += tmp [i + 4]; tmp [i] += tmp [i + 2]; tmp [i] += tmp [i + 1]; rij [i] += rij [i + 32]; rij [i] += rij [i + 16]; rij [i] += rij [i + 8]; rij [i] += rij [i + 4]; rij [i] += rij [i + 2]; rij [i] += rij [i + 1]; hij [i] += hij [i + 32]; hij [i] += hij [i + 16]; hij [i] += hij [i + 8]; hij [i] += hij [i + 4]; hij [i] += hij [i + 2]; hij [i] += hij [i + 1]; } if ( i == 0 ) { outData [ by*gridDim.x + bx ] = p[0]; outData [ by*gridDim.x + bx + gridDim.x*gridDim.y] = q[0]; outData [ by*gridDim.x + bx + 2*gridDim.x*gridDim.y] = tmp [0]; outData [ by*gridDim.x + bx + 3*gridDim.x*gridDim.y] = rij [0]; outData [ by*gridDim.x + bx + 4*gridDim.x*gridDim.y] = hij [0]; } }; At the very end, it is still necessary to add the results for all the blocks. Since the number of blocks is not very large, the result is more profitable to get on the processor. Since for each frame the shift is calculated independently, we can come up with an implementation when one core counts the shift for all frames, adding another dimension to the flow table for indexing the filter memory frames. However, it will be beneficial if the frames are small.
// . int numbCoeff = regInfo->nx / threads.x*regInfo->nx / threads.y; cudaMemcpy( coeffhost, coeffdev, numbCoeff*5* sizeof ( float ), cudaMemcpyDeviceToHost ); float q = 0, p = 0; float u = 0, v = 0, w = 0; for( int i = 0; i < numbCoeff; i++ ) { p += coeffhost[ i ]; q += coeffhost[ i + numbCoeff]; u += coeffhost[ i + 2*numbCoeff]; v += coeffhost[ i + 3*numbCoeff]; w += coeffhost[ i + 4*numbCoeff]; } dx = ( q * w - p * v )/( u * w - v * v ); dy = ( p * u - q * v )/( u * w - v * v ); What are the main disadvantages here.
1. The final result we get on the processor.
2. The coefficients for the reference frame rij, gij, hij are repeatedly calculated for each frame.
Let's look at the result in the profiler and evaluate whether this implementation works well. The profiler tells us that the read requests are merged, and the instructions take up most of the time.
Offset Search Core:

Core to whitewash staff:

Work time and optimization
Since the old GTX8800 was on a different computer and had already gone somewhere, I’m bringing results for the GTX Titan.
For frames of size 512x512, the following work time results were obtained. The core for calculating the shift coefficients takes 60 μs. If we add to it the copying of the coefficients and the final summation, we get 130 μs. With a memory of 20 frames, the running time is 2.6 ms, respectively. The whitening function takes 156 µs. There is also a function for calculating the coefficients on the processor; this is another 50 µs. The total is 2.806 ms.
Accordingly, on the CPU, the calculation of shifts takes 40 ms, the whitening of the frame is 30 ms and the calculation of the coefficients is another 50 μs. In total, it turns out 70 ms, which is 25 times slower than on the GPU (in fact, it is not, but more on that later).
The implementation is quite simple and is compatible with SS = 1.0. Let's now see what can be fixed. The last action in the search for shifts can be changed and implemented through atomic operations, which will work several times faster.
The modified code now looks like this:
// if ( i == 0 ) { atomicAdd( &outData[0], p[0] ); atomicAdd( &outData[1], q[0] ); atomicAdd( &outData[2], tmp[0] ); atomicAdd( &outData[3], rij[0] ); atomicAdd( &outData[4], hij[0] ); } // CPU float p = coeffhost[ 0 ]; float q = coeffhost[ 1 ]; float u = coeffhost[ 2 ]; float v = coeffhost[ 3 ]; float w = coeffhost[ 4 ]; dx = ( q * w - p * v )/( u * w - v * v ); dy = ( p * u - q * v )/( u * w - v * v ); In this case, the core takes about the same time, 66 µs.
You can get rid of multiple recounting rij, gij, hij by writing a separate kernel to calculate them, but then you have to load them every time, and this is three times more memory, since instead of loading one reference frame you will have to load three frames with coefficients. The optimal solution would be to make one core to calculate all the shifts at once, making a frame-by-frame loop inside the core.
Suppose that we have a more general task and could not have done so, and it would have been necessary to launch the kernel many times. At this point, you might think that everything is fine, the cores are written as a whole optimally, and the acceleration turned out up to 25 times, but if you look at the profiler, we will see the following picture:

Our functions on the GPU work only a small amount of time, the rest is delays, copying memory and other intermediate operations. In total, it raises 11.5 ms to calculate the offsets for all frames. As a result, the acceleration turned out only 6 times relative to the CPU. Remove all intermediate calculations and run the kernels one after the other in a loop:
for( int j = 0; j < regressInfo->memory - 1; j++ ) kernelShift<<< SKblocks, SKthreads >>> ( … ); After optimization, the profiler shows a completely different picture.

Much nicer turned out, really? .. Now the part with the calculation of shifts takes 1.40 ms instead of 11.5 ms. There remained a small interval between the cores of 4 µs, which is given by the profiler. And now let's try to run the kernel in different threads.
// stream for( int it = 0; it < 4; it++ ) cudaStreamCreate( &streamTX[it] ); …… for( int j = 0; j < regressInfo->memory - 1; j++ ) kernelShift<<< SKblocks, SKthreads, 0, streamTX[j%4] >>> (…); Now the profiler shows this result and here the interval is 1.22 ms.

And it is even less by 0.12 ms than 0.066 * 20 = 1.320.
The processor load is 84%.

As a result, the total time is 1.22 ms + 50 μs + 156 μs = 1.426 ms, which is 50 times faster than on the CPU.
Of course, it would be more correct to write one core for calculating shifts, but this is another way of optimization, and we considered a more general way, which cannot be underestimated. You can write a good implementation on the GPU, but forget about optimizing interaction with the GPU. The less time it takes for the kernel to work, the more the intervals between calls in which there are any actions on the CPU will be affected.
Filtration results
For example, images of the starry sky were taken, a moving dim object was added to them, small vibrations and self-noise.
Before processing:

After treatment:

Before processing:

After treatment:

In addition to the algorithm, it is possible and even necessary to add the function of deleting an object from previous frames, since it can badly spoil the result of filtering, leaving traces behind.
Unfortunately, the real recording did not work out, but if it works out and it will be interesting for readers, I will write about the results.
PS Found 4GB 10Mpix frames with a wide-angle camera. I'll try to process.
1. Work with memory in CUDA.
2. The algorithm for calculating the amount of CUDA.
Source: https://habr.com/ru/post/210286/
All Articles