Kepler equation: reboot

Good day! Recently, a post about the Kepler equation skipped here and I was slightly amazed that nothing was written about how it was generally deduced and from where, both historically and mathematically. As is known, Kepler brought him out of the observation of the motion of the planets, while Landau and Lifshits brought the motion of the planets out of ...


No theoretical mechanics is possible without the Lagrange function. I will not give her conclusion, I will just say that the whole point is in Hamilton’s least action,

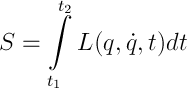
according to which, the mechanical system moves in such a way that the above integral, which, by the way, is called an action, has the smallest possible value. Perhaps, “varying the functional” tells you something - if so, then the Lagrange equation (UL) (1), which is the Euler equation, for a free particle follows from there — this is one of its variants. If not, then everything is a bit worse, namely: we would disassemble Newton's second law, spend about two pages on calculations, introduce the notions of generalized coordinates and forces and connections, and ultimately come to the same option. By the way, it is in the second way that the Lagrange function (PL) (2) is introduced in a natural way, as the difference between kinetic and potential energies.


')


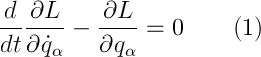
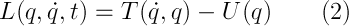
Concerning the notation, q is a generalized coordinate, a point is a derivative with respect to time. Important! According to the Lagrange formalism, generalized coordinates and velocities are independent quantities! In the case of a free particle (or a closed system, that is, a system that is not affected by external forces):



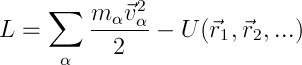
The indices of the generalized coordinates mean that in general it is a system of differential equations for each coordinate separately.
In short and in the opposite direction, replacing the generalized coordinates with radius vectors and velocities:



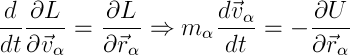
we obtain the Newton equation from the Lagrange equation (remembering that the derivative of the radius vector with respect to time is equal to velocity).

It is worth adding that the PL is additive, which means the PL of the system is the sum of the PL of its parts:



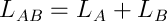
Great, we have a foundation. Now, to get to the Kepler equation, it is necessary to build walls — generalized energy, momentum, and angular momentum. Here it is important to make a small statement, which is actually very large and has the name “Noether theorem”: our space, at least on the scale of the bodies that we describe:

• uniformly
• isotropic
• has a uniform time.

Thus, we can introduce three laws of conservation, three integrals of motion, that is, a quantity conserved during motion, which depends exclusively on the initial conditions.

Let's start with the generalized energy. The most obvious thing I can do is get her out. We take advantage of the homogeneity of time, namely: FL does not depend explicitly on time, take the full derivative of the FL and transform, substituting the UL:



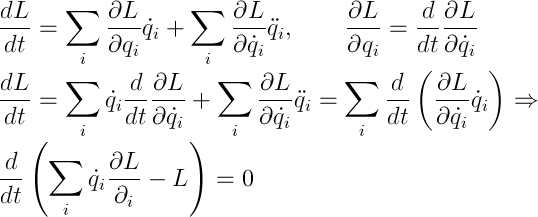
Where it comes from



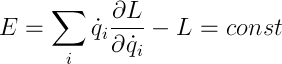
Is done. By the way, mechanical systems with conserved energy are called conservative.

The preservation of a generalized impulse follows from the homogeneity of space, and specifically from the freedom of parallel transport of the system in space. Consider the infinitesimal transfer of the system in space to epsilon, i.e. radius vectors of parts of the system will change as (1). The change in the PL is written as (2), which, by virtue of arbitrariness, epsilon can be rewritten as the zero sum of the partial derivatives. Then it is simple, (3) and we see that the total impulse (4) does not change when moving.



Here we introduce the concept of inertia center. In general, the mechanical system is intuitively representable in the form of a certain point moving along a straight line and other bodies that are already moving in some way relative to this point. So this point is the center of inertia, that is, we represent the closed mechanical system as a certain point with total mass, and shove everything else into the internal energy of the system.

With the impulse moment, it is the moment of the momentum, everything turns out in a similar way, so I just write out the result:



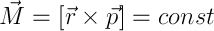
To summarize: we have the UL, the FL, and three integrals of motion: energy, momentum, and angular momentum.

We can finally move on to what I am taking away your time :) From what the Kepler equation in particular case follows is called the “two-body problem”. To begin with, simplify it. We write the PL of two bodies (1) and introduce the vector of their mutual distance (2). At the same time we will place the origin of coordinates in the center of inertia, which will give (3). From the second and third equations, we find the radius vectors of both points (4) and substitute them into the first (5). The reduced mass (6) is entered here.
Thus, the problem of two bodies is reduced to the problem of one body in some central field.



Consider the angular momentum in the central field M = [rp]. From here, M and r are perpendicular, and from the constancy of M (integral of motion, remember?), It is clear that the radius vector of the system always lies in the same plane - we have a flat motion, which means it’s time to introduce a cylindrical coordinate system with a center in the force center (sorry for tautology) and the z axis, perpendicular to the plane of motion, is essentially polar. Rewrite FL:



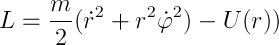
and look at the coordinate 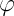- it is not! There is only its time derivative, which gives us the right to call it cyclical and say that the generalized impulse corresponding to it is preserved, and the solution of the problem is simplified. In this case, it coincides with the moment of momentum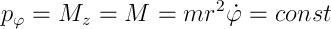



Also, the time does not explicitly enter the PL, which means that the energy of the system is also conserved. After a series of calculations



we obtain the solution of the problem in quadratures, that is, in the integrals. At the same time we introduce the effective potential energy



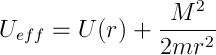
And what have the Kepler equation, the question from the back rows is heard. Well, well, persuaded, I was just about to ...

Let's consider the motion problem in the central potential field.



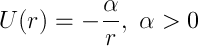
The minus sign indicates attraction (and the plus sign would mean repulsion, which in this case is not interesting to us - the particle will be reflected and go to infinity). This task even has its own name - yes, Kepler’s task. Construct the effective potential energy and its schedule. Obviously, when r tends to zero, it tends to infinity, and when the radius vector tends to infinity, respectively, to zero.



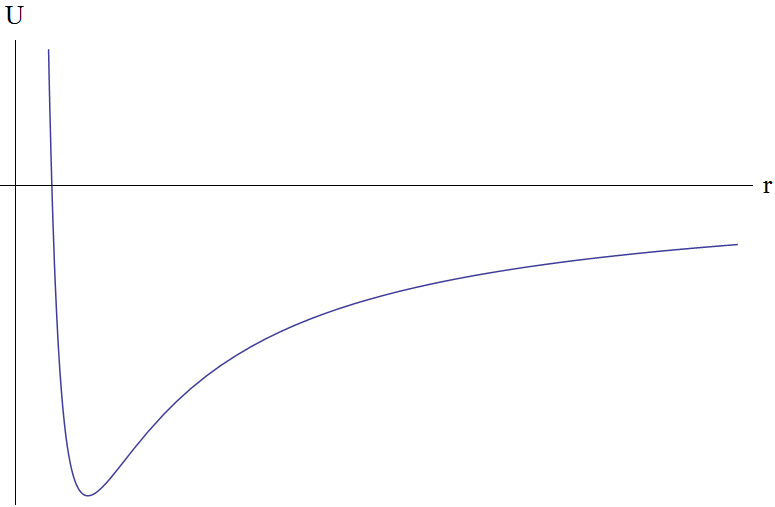
It is obvious from the graph that when the energy is E> 0, the motion will be infinite, that is, the particle will go to infinity, and if E <0, it will be finite. The shape of the trajectory will be determined by the general formula



which after substitution of a potential in it, the introduction of a pair of symbols



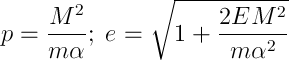
transform and select the origin of the angle so that const = 0, becomes



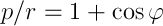
where p and e are the parameter and eccentricity of the orbit, respectively. Here it is, the Kepler equation.



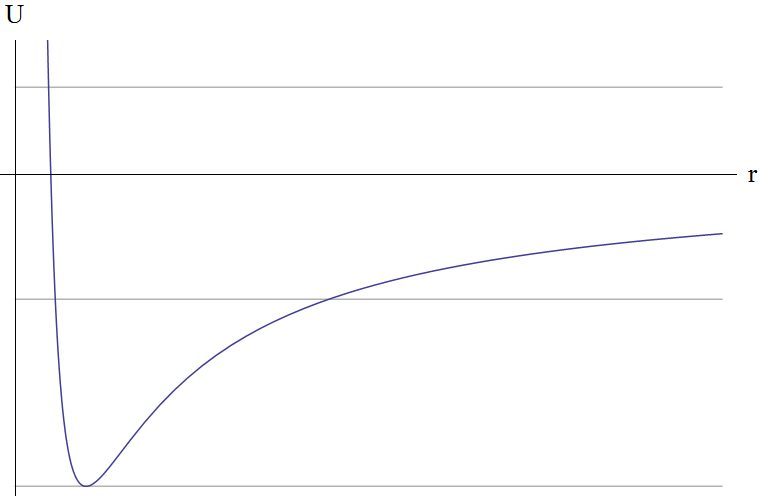
Let's analyze the results. To do this, once again look at the graph of the effective potential energy.

Gray lines - possible values ​​of the system energy. That is, they, of course, are possible everything, except smaller 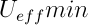, but we consider these. Down up:

• the lowest point is the minimum point. E <0, e = 0 - the trajectory of movement is a circle. The case is rare and very simple.
  
• a little higher. E <0, 0 <e <1 is an ellipse. The movement is finite, it is also possible to define the major and minor semiaxes of the ellipse as
  
  
  
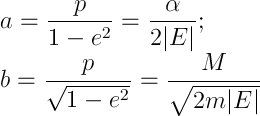
  which follows directly from the formulas of analytic geometry (here I, perhaps, will send you to Vygodsky or closer to Wiki). The smallest and greatest distances to the focus of the ellipse, perihelion and aphelium, respectively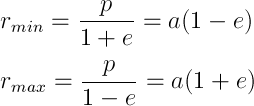
  
  
  
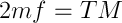  what could, generally speaking, get in the forehead from . The orbital rotation time is obtained from Kepler's second law. . For ellipse sector speed 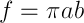which means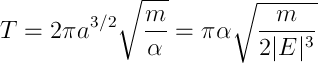
  
  
  
  So we got the third law of Kepler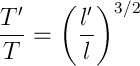
  
  .
  
  It should be noted here that the period depends only on the particle energy.
  
• E = 0, e = 1. The trajectory is infinite, this is a parabola with 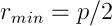. Such a trajectory will be for a particle moving from infinity from a state of rest.
  
• E> 0, e> 1. The trajectory is again infinite, but this time it is hyperbole, with perihelion
  
  
  

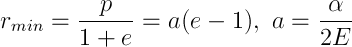
Perhaps this is all that I would like to tell you about one of the fundamental problems of mechanics. The Kepler problem is often used to test mathematical modeling systems, as very well studied and at the same time simple. Together with the harmonic oscillator problem, this is one of two problems about a body moving along a closed trajectory, when the body returns to the initial point with the same speed. The Kepler problem is used to construct new methods of classical mechanics, in particular, the Hamiltonian formalism, the Hamilton-Jacobi equation, and the action-angle variable system.