Calculating intersecting intervals in linear and closed namespaces
Hello! And at once I apologize for the too tricky name, but it most fully reflects the material presented below.
I think many of you have come across the need to calculate overlapping intervals. But the task I faced the other day turned out to be not so trivial. But first things first.
If you already have an idea about the intersection of intervals, then go straight here .
The calculation of the intersections of time intervals (time intervals) on a straight line of time is not difficult. We can conditionally have five types of temporary intersections.
We denote one time interval as "\ \" and the other as "/ /"
')
Thus, we can express each specific intersection using the signs <,> and =. And having in the arsenal of the signs <= and> = we can reduce the number of templates for calculating to four (by growing up, thus, “occurrence” and “coincidence” or “absorption” and “coincidence” or even “displacement” and “coincidence”) . In addition, either “occurrence” or “absorption” (but not both) can also be eliminated, considering it a particular case of “displacement”.
So, having a table of the form:
To select from the table all users crossing the specified interval (say 4-8), use the query:
This query will return the first, second and third users. It's pretty simple.
Hm And what if you need to choose non-overlapping intervals?
In fact, it is still simpler: in contrast to the intersection, there are only two cases of NOT intersection:
and on a continuous time line we only need to check if the end of one interval is less than the beginning of another.
And the SQL query is reduced to
And here we are reminded of the denial of expressions. If computing non-intersections is much easier than intersections, then why not just drop all non-intersections?
We open brackets (thanks Yggaz ):
Woo-la! Everything is much more concise!
All this is very beautiful, and it works wonderfully ... as long as the time line is straight.
We figured out the calculations on the timeline. So what is a “closed” namespace?
This is a namespace, which, when the first order names are exhausted, does not move to a new order, but returns to its beginning.
Linear namespace:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, ...
Closed namespace:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 0, 1, 2, 3, 4, ...
Suppose we have a table with a schedule of work (let it be a 24-hour call center):
* minutes "00" omitted for ease of expression
I work from 10 to 19 and I want to know exactly which workers will cross my work schedule.
We make a sample given earlier scheme:
All perfectly! I got the data of three workers, whose interval overlaps with mine.
Ok, what if I work at night? Suppose from 20 to 6? That is, the beginning of my interval is greater than its end. A sample of the table for these conditions will return a complete nonsense. That is, the collapse happens when my time interval crosses the “zero” mark of the day. But after all, intervals crossing the “zero” mark can be stored in the database.
I ran into a similar problem two days ago.
The problem of sampling intervals by the linear method from the table with non-linear structure data was on the face.
The first thing that occurred to me was to expand the space of the day to 48 hours, thereby getting rid of the “zero” mark. But this attempt failed - because the intervals between 1 and 3 could not get into the sample between 22 and 27 (3). Eh! Now, if I had a twenty-fourfold number system, I would simply remove the second-order mark and everything.
I attempted to find a solution to this problem on the Internet. Information on the intersection of the intervals on the "linear" time was plenty. But either this question was not widely discussed, or the SQL gurus kept the decision “for themselves” - there was no solution for a closed system anywhere.
In general, after asking the gurus for advice from the forums, I got a solution: it was necessary to divide the intersecting “zero” intervals into two parts, thereby obtaining two linear intervals, and to compare them both with the intervals in the table (which also needed to be divided if they cross zero). The solution worked and was quite stable, although it was cumbersome. However, it did not leave me feeling that everything was "much simpler."
So, highlighting a couple of hours for this question, I took a notebook and a pencil ... I give you what I did:
The bottom line is that the day - there is a closed line of time - a circle.
And time intervals - the essence of the arc of this circle.
Thus, to negate non-intersections (see the first part of the post), we can construct a couple of non-intersection schemes:

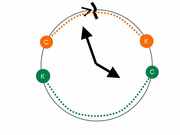
In the first case, we have the usual linear scheme for negating non-intersections. In the second one of the arcs suppresses the "zero" mark. There is a third case that can be immediately taken as an intersection (without negating non-intersections):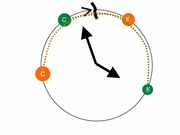 Both intervals intersect the "zero" mark, and therefore intersect by definition. In addition, there are two more cases where the intervals (entered and taken from the table) are “swapped” by places.
Both intervals intersect the "zero" mark, and therefore intersect by definition. In addition, there are two more cases where the intervals (entered and taken from the table) are “swapped” by places.
Having conjured a little with the base (somewhere even by the method of highly scientific spear), I managed to collect such a query:
And a simplified version of the comment from kirillzorin :
The query is quite efficient and, what is most funny, is valid for any closed number systems - be it an hour, a day, a week, a month, a year. And yet, this method does not use "crutches", such as additional fields.
Most likely, I invented the bicycle. But due to the fact that I myself did not find such information when I needed it - I assume that this method is not too widely covered. This is where my story ends.
I think many of you have come across the need to calculate overlapping intervals. But the task I faced the other day turned out to be not so trivial. But first things first.
Calculating intersecting intervals in a linear namespace
If you already have an idea about the intersection of intervals, then go straight here .
The calculation of the intersections of time intervals (time intervals) on a straight line of time is not difficult. We can conditionally have five types of temporary intersections.
We denote one time interval as "\ \" and the other as "/ /"
')
- Offset forward along the time axis "/ \ / \"
- Offset back along the time axis "\ / \ /"
- Entry "/ \ \ /"
- Absorption "\ / / \"
- The match "XX"
Thus, we can express each specific intersection using the signs <,> and =. And having in the arsenal of the signs <= and> = we can reduce the number of templates for calculating to four (by growing up, thus, “occurrence” and “coincidence” or “absorption” and “coincidence” or even “displacement” and “coincidence”) . In addition, either “occurrence” or “absorption” (but not both) can also be eliminated, considering it a particular case of “displacement”.
So, having a table of the form:
| user | start | end |
| user1 | 2 | 7 |
| user2 | five | 9 |
| user3 | eight | eleven |
| user4 | one | 12 |
To select from the table all users crossing the specified interval (say 4-8), use the query:
SET @start:=4; SET @end:=8; SELECT * FROM `table` WHERE (`start` >= @start AND `start` < @end) /* */ OR (`end` <= @end AND `end` > @start) /* */ OR (`start` < @end AND `end` > @start) /* - */ OR (`start` >= @start AND `end` <= @end)/* */ This query will return the first, second and third users. It's pretty simple.
Hm And what if you need to choose non-overlapping intervals?
In fact, it is still simpler: in contrast to the intersection, there are only two cases of NOT intersection:
- Offset back "\ \ / /"
- Offset forward "/ / \ \"
and on a continuous time line we only need to check if the end of one interval is less than the beginning of another.
And the SQL query is reduced to
SET @start:=4; SET @end:=8; SELECT * FROM `table` WHERE `start` >= @end OR `end` <= @start /* */ And here we are reminded of the denial of expressions. If computing non-intersections is much easier than intersections, then why not just drop all non-intersections?
WHERE NOT ( `start` >= @end OR `end` <= @start ) We open brackets (thanks Yggaz ):
WHERE `start` < @end AND `end` > @start Woo-la! Everything is much more concise!
All this is very beautiful, and it works wonderfully ... as long as the time line is straight.
Calculating overlapping intervals in closed namespaces
We figured out the calculations on the timeline. So what is a “closed” namespace?
This is a namespace, which, when the first order names are exhausted, does not move to a new order, but returns to its beginning.
Linear namespace:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, ...
Closed namespace:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 0, 1, 2, 3, 4, ...
Suppose we have a table with a schedule of work (let it be a 24-hour call center):
* minutes "00" omitted for ease of expression
| usrer | start | end |
| usrer1 | 0 | 6 |
| usrer2 | 6 | 12 |
| usrer3 | 12 | 18 |
| usrer4 | 18 | 23 |
I work from 10 to 19 and I want to know exactly which workers will cross my work schedule.
We make a sample given earlier scheme:
SET @start:=10; SET @end:=19; SELECT * FROM `table` WHERE NOT ( `start` >= @end OR `end` <= @start ) All perfectly! I got the data of three workers, whose interval overlaps with mine.
Ok, what if I work at night? Suppose from 20 to 6? That is, the beginning of my interval is greater than its end. A sample of the table for these conditions will return a complete nonsense. That is, the collapse happens when my time interval crosses the “zero” mark of the day. But after all, intervals crossing the “zero” mark can be stored in the database.
I ran into a similar problem two days ago.
The problem of sampling intervals by the linear method from the table with non-linear structure data was on the face.
The first thing that occurred to me was to expand the space of the day to 48 hours, thereby getting rid of the “zero” mark. But this attempt failed - because the intervals between 1 and 3 could not get into the sample between 22 and 27 (3). Eh! Now, if I had a twenty-fourfold number system, I would simply remove the second-order mark and everything.
I attempted to find a solution to this problem on the Internet. Information on the intersection of the intervals on the "linear" time was plenty. But either this question was not widely discussed, or the SQL gurus kept the decision “for themselves” - there was no solution for a closed system anywhere.
In general, after asking the gurus for advice from the forums, I got a solution: it was necessary to divide the intersecting “zero” intervals into two parts, thereby obtaining two linear intervals, and to compare them both with the intervals in the table (which also needed to be divided if they cross zero). The solution worked and was quite stable, although it was cumbersome. However, it did not leave me feeling that everything was "much simpler."
So, highlighting a couple of hours for this question, I took a notebook and a pencil ... I give you what I did:

The bottom line is that the day - there is a closed line of time - a circle.
And time intervals - the essence of the arc of this circle.
Thus, to negate non-intersections (see the first part of the post), we can construct a couple of non-intersection schemes:


In the first case, we have the usual linear scheme for negating non-intersections. In the second one of the arcs suppresses the "zero" mark. There is a third case that can be immediately taken as an intersection (without negating non-intersections):
 Both intervals intersect the "zero" mark, and therefore intersect by definition. In addition, there are two more cases where the intervals (entered and taken from the table) are “swapped” by places.
Both intervals intersect the "zero" mark, and therefore intersect by definition. In addition, there are two more cases where the intervals (entered and taken from the table) are “swapped” by places.Having conjured a little with the base (somewhere even by the method of highly scientific spear), I managed to collect such a query:
SET @start:= X ; SET @end:= Y; SELECT * FROM `lparty_ads` WHERE ((`prime_start` < `prime_end` AND @start < @end) AND NOT (`prime_end`<= @start OR @end <=`prime_start` ) OR (( (`prime_start` < `prime_end` AND @start > @end) OR (`prime_start` > `prime_end` AND @start < @end)) AND NOT ( `prime_end` <= @start AND @end <= `prime_start` )) OR (`prime_start` > `prime_end` AND @start > @end)) And a simplified version of the comment from kirillzorin :
set @start := X; set @end := Y; select * from tab where greatest(start, @start) <= least(end, @end) or ((end > @start or @end > start) and sign(start - end) <> sign(@start - @end)) or (end < start and @end < @start); The query is quite efficient and, what is most funny, is valid for any closed number systems - be it an hour, a day, a week, a month, a year. And yet, this method does not use "crutches", such as additional fields.
Most likely, I invented the bicycle. But due to the fact that I myself did not find such information when I needed it - I assume that this method is not too widely covered. This is where my story ends.
Source: https://habr.com/ru/post/209138/
All Articles