Simple battle model on Modelica

Good day! Having recently learned about a modeling tool such as the Modelica language and its free implementation of OpenModelica , I was surprised that there is only one article on Habré. Since the topic is somewhat unusual, the details had to be comprehended on
Note: for the preparation of the article, the last nightly build of OpenModelica (rev18625) was used. When installing, note that you need to specify the path without spaces.
')
Task
Imagine a war as a process in which two adversaries, possessing different forces (in terms of proportion, but not in strength), achieve the same goal - to capture as large enemy territory as possible by destroying the enemy forces on it. For definiteness, we will assume that the territory was conquered when the infantry set foot on it (ground forces). The sea is not included in the territory. Victory is counted when the entire territory of the enemy is conquered.
Generally speaking, wars also include economics, but modeling this would take too much space. For now, let us consider three types of forces: sea, land, and aviation (we will not consider nuclear weapons either). Each has resistance to attack, or health (one unit), as well as the actual attack power (we will measure, say, the number of bullets). And let every few units of time, new units come into battle.
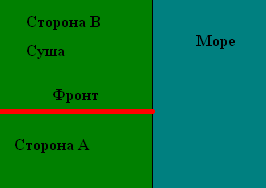
The fighting takes place in a square, across which the front line runs horizontally, and to the right is the sea, where actions are carried out by ships. The length of the side of the square is denoted by L (for definiteness, we take as 100 kilometers). Then the area conquered by side A will be equal to A * L, conquered by the adversary - (LA) * L. The change to A will depend on the correlation of forces. The greater the forces at the front prevail, the more A changes (in favor of those forces that are greater). Let's say for definiteness, a unit of infantry on one side advances a front (if without a fight) by 1 kilometer per unit of time.
Concepts Modelica
The basis of modeling in Modelica are the classes (and their variations according to the options of the announcement / application, but more on that a bit later). A class in Modelica is somewhat different from the classes we are used to, since it contains not only fields and methods (in Modelica, functions), but also equations that relate variables to each other. Also, the fields can have a different type of "variability" - a constant (and there is a constant), a parameter (does not change in the current simulation), and, in fact, a variable. A field in a class can be either an object of built-in types (Boolean, Real, etc.) or user-defined types. A more complex concept is the possibility of “template” - the replacement of the field type, its redefinition.
Classes can be inherited (including multiple, and only diamond). For Modelica, this means that all the contents of the inheritance are copied into the inherited class, including the equations. And here we should mention the basic rule of Modelica - the number of equations for variables must correspond to the number of variables. No more, no less.
An example of solving the problem
The simplest type of class - record - cannot contain equations.
First, we define the abstract type of a combat unit.
UnitData.mo
record UnitData "Abstract army unit record" parameter Real unitHealth; parameter Real unitAttack; parameter Real supplyTime; parameter Real supplyNumber; end UnitData; This code declares four non-initialized parameters. In quotes, after declaring classes and variables, you can add document strings. In general, the comments in Modelica - C ++ - style, that is, // or / * / * (comments of this kind are ignored by the environment).
The next step is to declare a class with equations, the objects of which will be some military forces, characterized by the same as combat units + numbers.
Forces.mo
class Forces "Abstract army forces class" extends UnitData; parameter Real startNumber = 0; Real number (start = startNumber); Boolean destroyed; equation destroyed = number < 0; when destroyed then reinit(number, 0); end when; when sample(supplyTime, supplyTime) then reinit(number, pre(number) + supplyNumber); end when; end Forces; Using this file as an example, you can trace inheritance, as well as work with Modelica events.
If the equation is destroyed = number <0; should not cause questions, then inside the first when block a special operator reinit is used, which sets the value of the variable to the result of the expression with the second parameter. reinit, like pre (the value of the previous step), can only be used inside a when block. pre must be used so that the equation (namely, the equation) is not: x = x + 1.
The built-in function sample returns true if the simulation time (time) is equal to the first parameter (first call), and then at intervals equal to the second parameter (in our case they are equal - the help arrives at equal intervals from the moment of supplyTime).
Next we need a class representing the enemy army:
EnemyForces.mo
class EnemyForces "Enemy forces references" replaceable Forces enemyAir; replaceable Forces enemySea; replaceable Forces enemyLand; end EnemyForces; Specifying a variable as replaceable allows you to further override the type of the variable when declaring an EnemyForces object.
Now we come to the most important thing. Actually a class representing the army.
Army.mo
class Army class LandArmy = Forces(unitHealth = 100, unitAttack = 400, supplyTime = 0.25, supplyNumber = 800); class AirArmy = Forces(unitHealth = 400, unitAttack = 750, supplyTime = 0.5, supplyNumber = 400); class SeaArmy = Forces(unitHealth = 3000, unitAttack = 7000, supplyTime = 1, supplyNumber = 20); SeaArmy seaArmy; AirArmy airArmy; LandArmy landArmy; EnemyForces enemyForces (redeclare Army.AirArmy enemyAir, redeclare Army.SeaArmy enemySea, redeclare Army.LandArmy enemyLand); Real armyForce; equation armyForce = seaArmy.unitHealth * seaArmy.number + airArmy.unitHealth * airArmy.number + landArmy.unitHealth * landArmy.number; der(seaArmy.number) = if not seaArmy.destroyed then -(enemyForces.enemyAir.number * enemyForces.enemyAir.unitAttack + enemyForces.enemySea.number * enemyForces.enemySea.unitAttack) / seaArmy.unitHealth else 0; der(airArmy.number) = if not airArmy.destroyed then -(enemyForces.enemyAir.number * enemyForces.enemyAir.unitAttack + enemyForces.enemySea.number * enemyForces.enemySea.unitAttack + enemyForces.enemyLand.number * enemyForces.enemyLand.unitAttack) / airArmy.unitHealth else 0; der(landArmy.number) = if not landArmy.destroyed then -(enemyForces.enemyAir.number * enemyForces.enemyAir.unitAttack + enemyForces.enemyLand.number * enemyForces.enemyLand.unitAttack) / landArmy.unitHealth else 0; end Army; What's going on here. First, we create specific classes of the armed forces, simply equating them with the existing Forces class and initializing its parameters. Immediately declare objects. The next thing is to create an object that will be used as a reference to the enemy army, and replace the replaceable variables with the redeclare keyword. Variable armyForce we will need purely for "analytical conclusions".
About equations - the first equation means that the strength of the army is the armor of all units that are.
The following three equations mean:
- If the naval army is not destroyed, then at each moment of time from all its armor decreases the damage inflicted by air and sea forces
- If the air army is not destroyed, then at each moment of time from all its armor the damage caused by any enemy troops decreases,
- Similarly with ground forces, except that the naval forces do not cause damage to them.
The notation der (var) is a time derivative of var (variable).
And finally, we describe the armed conflict itself.
Conflict.mo
model Conflict "Conflict of two armies model" parameter Real armyASea = 200; parameter Real armyAAir = 1000; parameter Real armyALand = 4000; parameter Real armyBSea = 100; parameter Real armyBAir = 1800; parameter Real armyBLand = 3600; Army armyA ( seaArmy.startNumber = armyASea, airArmy.startNumber = armyAAir, landArmy.startNumber = armyALand, enemyForces.enemyAir.startNumber = armyBAir, enemyForces.enemySea.startNumber = armyBSea, enemyForces.enemyLand.startNumber = armyBLand ); Army armyB ( seaArmy.startNumber = armyBSea, airArmy.startNumber = armyBAir, landArmy.startNumber = armyBLand, enemyForces.enemyAir.startNumber = armyAAir, enemyForces.enemySea.startNumber = armyASea, enemyForces.enemyLand.startNumber = armyALand ); parameter Real L = 100; parameter Real landArmySpeed = 1; Real A (start = L / 2); equation armyA.enemyForces.enemyAir.number = armyB.airArmy.number; armyA.enemyForces.enemySea.number = armyB.seaArmy.number; armyA.enemyForces.enemyLand.number = armyB.landArmy.number; armyB.enemyForces.enemyAir.number = armyA.airArmy.number; armyB.enemyForces.enemySea.number = armyA.seaArmy.number; armyB.enemyForces.enemyLand.number = armyA.landArmy.number; when A > L then terminate("Army A wins"); end when; when A < 0 then terminate("Army B wins"); end when; der (A) = (armyA.landArmy.number - armyB.landArmy.number) * landArmySpeed / L; end Conflict; The keyword model is used here. This is also a class, but only models can be used for optimization (about which later).
In addition to declaring warring parties, which we will not dwell on, there are equations that establish that enemy A is B, and vice versa. Two when-conditions mean terminating a simulation with a mark of what happened.
Launch and Results
In order to run the model, you can use the shell OpenModelica, typing the following in it:
Shell commands OpenModelica
loadModel(Modelica) loadFile("d:/path/UnitData.mo") loadFile("d:/path/Forces.mo") loadFile("d:/path/EnemyForces.mo") loadFile("d:/path/Army.mo") loadFile("d:/path/Conflict.mo") simulate(Conflict, stopTime = 2) plot({armyA.armyForce, armyB.armyForce}, xRange = {0, 2}) plot({armyA.landArmy.number, armyB.landArmy.number, armyA.seaArmy.number, armyB.seaArmy.number, armyA.airArmy.number, armyB.airArmy.number}, xRange = {0, 2}) plot(A, xRange = {0, 2}) Relevant constructions are shown in the pictures below.
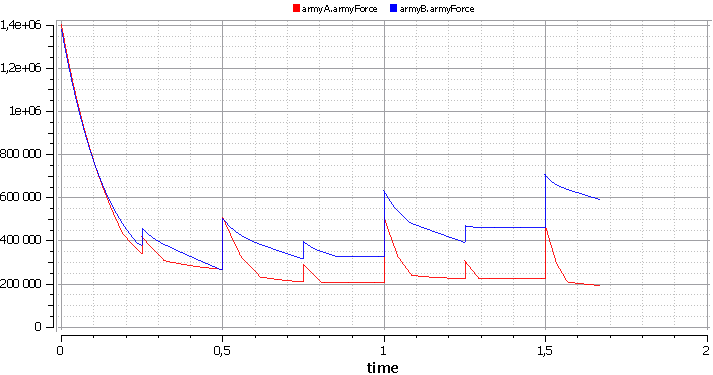
This is the correlation of forces in time.
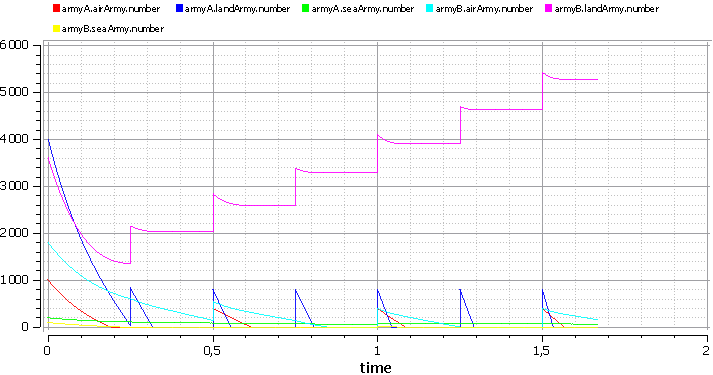
This is the ratio of forces in time in the context of the types of troops.
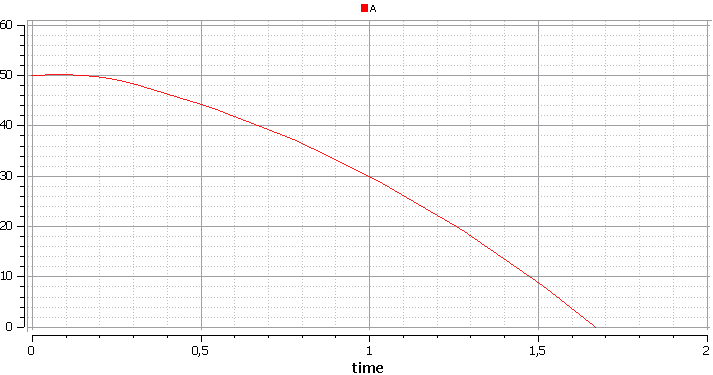
And so - the front line. From the graphs it is clear that army A first won, but then army B won it.
Optimization with OpenModelica
Besides the fact that you can simulate, you can also find answers to the questions asked by the model. For example, if you ask yourself what is the minimum initial number of ground forces, Army B will win, then with the help of OMOptim tool included in OpenModelica you can get the following picture:
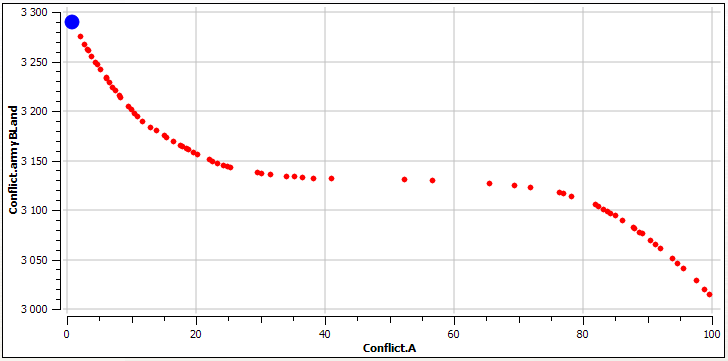
Instead of conclusion
OpenModelica is well documented, for those who are familiar with English. Overall, the tool is promising. While the error messages are not very talking, and the debug information is not to say that it is easily interpreted. But on the whole, with enough time and interest, everything is victorious.
Still instead of the conclusion
It is clear that the battle model is very simple, and the reality, if it reflects, is only in the fact that (in our case, the minimum) the strength in forces can not guarantee victory, and the final result is determined by the structure of the system (who beats someone) to a lesser degree than the initial conditions.
useful links
Excellent tutorial (in English).
Web Reference (in English).
UPDATE
After some time, I realized that to call her armor “the strength of the army” is somewhat hastily. However, light modifications:
Army.mo changes
class Army //... Real armyHealth, armyStrength; equation armyHealth = seaArmy.unitHealth * seaArmy.number + airArmy.unitHealth * airArmy.number + landArmy.unitHealth * landArmy.number; armyStrength = seaArmy.unitAttack * seaArmy.number + airArmy.unitAttack * airArmy.number + landArmy.unitAttack * landArmy.number; //... end Army; You can come to the picture, which will confirm the already stated conclusions.
Schedule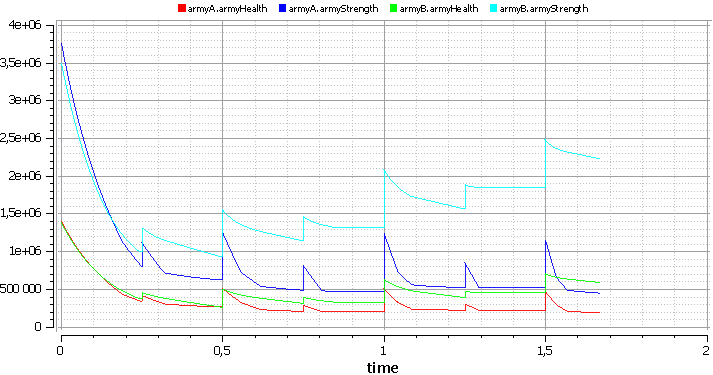

Source: https://habr.com/ru/post/209112/
All Articles