Kepler equation
The articles on celestial mechanics are somewhat popular on Habré, so I decided to tell
about one fundamental equation of motion, namely, the Kepler equation.
As is known, the finite motion of celestial bodies in the solar system occurs in an ellipse. However, if necessary
to establish at what point the celestial body is at a given point in time, this information is not enough and it is necessary to use the Kepler equation.
We derive this equation.
Let me remind you that the ellipse is flattened by
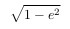
circle. Here, e is the eccentricity.
')
The area of the ellipse is equal to

where a is the big semi-axis.
According to Kepler’s second law, which states that the area swept by the radius vector of a celestial body is proportional to time, you can write

where T is the orbital period, t is the current time, t0 is the time of passage of the perihelion (the orbit point closest to the Sun).
Let us now find the dependence of this area on the position of the celestial body in orbit, that is, on the magnitude of the radius vector r and the true anomaly - the angle between perihelion and the celestial body, viewed from the Sun.
To do this, we introduce an additional variable - eccentric anomaly E.
We direct the x axis from the Sun (the origin), which is located in one of the foci of the ellipse, towards the perihelion along the apsid line (the straight line connecting the pericenter with the apocenter).
We also create an auxiliary circle with a radius equal to the major semi-axis of the ellipse.

The abscissa of a celestial body at point P will be equal to

the ordinate will be equal to

So we get
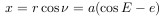
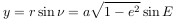
To calculate the area S, consider the auxiliary figures:
P'-O-Per circle sector:
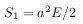
PO-Per ellipse sector:
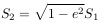
Triangle O-O'-P:

P-O'-Per Sector:

From here, area S is equal to:
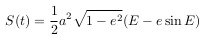
Comparing this expression with Kepler’s earlier deduction from the second law,
we get:
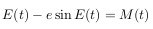
where M (t) = 2 * pi * (t - t0) / T
This is the Kepler equation.
Note that this transcendental equation for E and in the general case it is not possible to obtain an explicit solution.
To calculate the coordinates of a celestial body, it is necessary to find an eccentric anomaly by the known M and e, and then determine the radius vector and angle and, if necessary, x and y using the above formulas.
An interesting question is finding methods for solving the Kepler equation.
This was done by the best minds of humanity over the past four hundred years.
The result was the enrichment of mathematics with many interesting ideas, but the description of this requires a separate article.
about one fundamental equation of motion, namely, the Kepler equation.
As is known, the finite motion of celestial bodies in the solar system occurs in an ellipse. However, if necessary
to establish at what point the celestial body is at a given point in time, this information is not enough and it is necessary to use the Kepler equation.
We derive this equation.
Let me remind you that the ellipse is flattened by
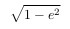
circle. Here, e is the eccentricity.
')
The area of the ellipse is equal to

where a is the big semi-axis.
According to Kepler’s second law, which states that the area swept by the radius vector of a celestial body is proportional to time, you can write

where T is the orbital period, t is the current time, t0 is the time of passage of the perihelion (the orbit point closest to the Sun).
Let us now find the dependence of this area on the position of the celestial body in orbit, that is, on the magnitude of the radius vector r and the true anomaly - the angle between perihelion and the celestial body, viewed from the Sun.
To do this, we introduce an additional variable - eccentric anomaly E.
We direct the x axis from the Sun (the origin), which is located in one of the foci of the ellipse, towards the perihelion along the apsid line (the straight line connecting the pericenter with the apocenter).
We also create an auxiliary circle with a radius equal to the major semi-axis of the ellipse.

The abscissa of a celestial body at point P will be equal to

the ordinate will be equal to

So we get
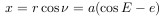
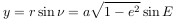
To calculate the area S, consider the auxiliary figures:
P'-O-Per circle sector:
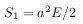
PO-Per ellipse sector:
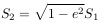
Triangle O-O'-P:

P-O'-Per Sector:

From here, area S is equal to:
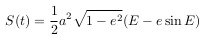
Comparing this expression with Kepler’s earlier deduction from the second law,
we get:
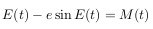
where M (t) = 2 * pi * (t - t0) / T
This is the Kepler equation.
Note that this transcendental equation for E and in the general case it is not possible to obtain an explicit solution.
To calculate the coordinates of a celestial body, it is necessary to find an eccentric anomaly by the known M and e, and then determine the radius vector and angle and, if necessary, x and y using the above formulas.
An interesting question is finding methods for solving the Kepler equation.
This was done by the best minds of humanity over the past four hundred years.
The result was the enrichment of mathematics with many interesting ideas, but the description of this requires a separate article.
Source: https://habr.com/ru/post/209106/
All Articles