The transport problem with the partisanship ("with trailers")
Required knowledge: familiarity with the methods of linear programming, methods for solving the transport problem (especially the method of potentials).
A year ago on the third
course as one of the laboratory work on the course "Methods of optimization" I was asked to implement the solution of the transport problem, but with one small condition: transportation takes place in batches. This means that now, unlike the classical production, the transportation of a consignment of goods (eg 10 pieces) is paid for, and even if you need to transport 11 pieces, you will pay for two lots (in one trailer, 11 pieces will not fit). It would seem a minor addition, but how now to solve the problem, but at least how to formalize it? As a student of the Department of Applied Mathematics, I was not used to the fact that the great google.ru does not know something, but what was my surprise when neither his elder brother - an English-speaking google, nor the darkness of the books on the theory of optimization I could answer the this question.
I just want to say - with the algorithm I do not pretend to the Fields Award. I do not propose anything supernatural, but I can give some help to those who are just starting to solve this problem.
Let C be the payment matrix, a be the vector of cargo stocks, b be the vector of cargo demand, k be the quantity of goods in a lot. We will consider the following formalization:
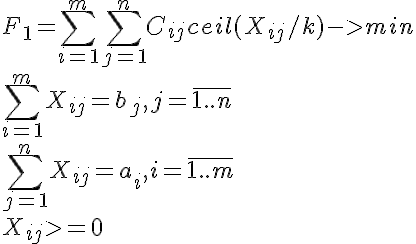
where X is the transport matrix, i.e. the parameter being optimized, and ceil - rounding up to the nearest integer.
Additionally we introduce into consideration:
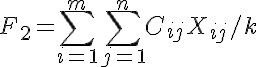
First, we solve the classical transport problem with F2-> min. The resulting value of F2 is the lower limit for F1 on the set of valid values. Remember the value of F2_save: = F2. Find the value of F1 at the obtained solution X and remember its F1_save = F1. If F1_save == ceil (F2_save), then X is the desired solution, otherwise we go further.
F1 can be reduced only by reducing the basic components of X to the nearest multiple k values , so we will build (the branch and bound method) a problem tree with additional constraints. The top of the tree is the solution already received. Each next tree tier is constructed as follows: for each basic component (xij) equal to some non-multiple k value (z), we solve the classical transport problem F2-> min with the additional constraint xij = [z / k] * k ([x] - the integer part of x) (see PS). If for the solution obtained, F1 <F1_save, then F1_save: = F1. If for the resulting solution ceil (F2)> = F1_save, then this branch will not continue. If F1 == ceil (F2_save), then the resulting X is the desired solution, otherwise we go further. Thus, we obtain a decision tree, each branch of which is completed if on the sheet of this branch ceil (F2)> = F1_save, or if all the components from the basis are multiple k or if the task had no solution at all. The plan that corresponds to that obtained after building the F1_save tree is optimal.
PS Adding a restriction does not necessarily solve the problem again. You can, for example, sort through all possible F1-reducing cycles and select the optimal one among them. Or use the methods of the dual simplex method.
')
Example
Consider the algorithm on a very simple example. Let k = 3, C = {{2,2}, {4,5}}, a = {2,3}, b = {2,3}. So the top of the tree is the solution of such a transportation problem with the objective function F2:
0) X = {{0,2}, {2,1}}, F2 (X) ~ = 5.67, F1 (X) = 2 + 4 + 5 = 11.
F2_save: = 5.67, F1_save: = 11
because ceil (5.67) <11 go further - we build the next tier of the tree:
1.1) we add the condition x12 == 0 to the problem solved at node 0 and solve it again.
X = {{2.0}, {0.3}}, F2 (X) ~ = 6.35, F1 (X) = 2 + 5 = 7.
because F1 <F1_save (7 <11), then F1_save: = 7
because ceil (F2)> = F1_save (7> = 7), then we don’t continue this branch
because F1> ceil (F2_save) go further (perhaps there is a better solution), the branch does not continue, but the tier is not finished yet.
1.2) we add the condition x21 == 0 to the problem solved at node 0 and solve it again.
X = {{2.0}, {0.3}}, F2 (X) ~ = 6.35, F1 (X) = 2 + 5 = 7.
because F1 == F1_save (7 == 7), then F1_save does not change
because ceil (F2)> = F1_save (7> = 7), then we don’t continue this branch
because F1> ceil (F2_save) go further (perhaps there is a better solution), the branch does not continue, but the tier is not finished yet.
1.3) we add the condition x22 == 0 to the problem solved at node 0 and solve it again. Such a task has no solution => and we do not continue this branch.
There are no more basic components left (the tier is completed) and there is no need to continue the branches (meaningless, we will not get a better solution), so the tree has been built. F1_save == 7 is our minimum cost. Plan for them the corresponding (he is the answer) X = {{2,0}, {0,3}}
A year ago on the third
course as one of the laboratory work on the course "Methods of optimization" I was asked to implement the solution of the transport problem, but with one small condition: transportation takes place in batches. This means that now, unlike the classical production, the transportation of a consignment of goods (eg 10 pieces) is paid for, and even if you need to transport 11 pieces, you will pay for two lots (in one trailer, 11 pieces will not fit). It would seem a minor addition, but how now to solve the problem, but at least how to formalize it? As a student of the Department of Applied Mathematics, I was not used to the fact that the great google.ru does not know something, but what was my surprise when neither his elder brother - an English-speaking google, nor the darkness of the books on the theory of optimization I could answer the this question.I just want to say - with the algorithm I do not pretend to the Fields Award. I do not propose anything supernatural, but I can give some help to those who are just starting to solve this problem.
Let C be the payment matrix, a be the vector of cargo stocks, b be the vector of cargo demand, k be the quantity of goods in a lot. We will consider the following formalization:
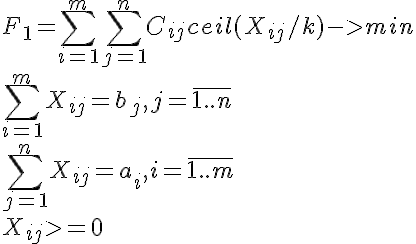
where X is the transport matrix, i.e. the parameter being optimized, and ceil - rounding up to the nearest integer.
Additionally we introduce into consideration:
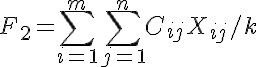
First, we solve the classical transport problem with F2-> min. The resulting value of F2 is the lower limit for F1 on the set of valid values. Remember the value of F2_save: = F2. Find the value of F1 at the obtained solution X and remember its F1_save = F1. If F1_save == ceil (F2_save), then X is the desired solution, otherwise we go further.
F1 can be reduced only by reducing the basic components of X to the nearest multiple k values , so we will build (the branch and bound method) a problem tree with additional constraints. The top of the tree is the solution already received. Each next tree tier is constructed as follows: for each basic component (xij) equal to some non-multiple k value (z), we solve the classical transport problem F2-> min with the additional constraint xij = [z / k] * k ([x] - the integer part of x) (see PS). If for the solution obtained, F1 <F1_save, then F1_save: = F1. If for the resulting solution ceil (F2)> = F1_save, then this branch will not continue. If F1 == ceil (F2_save), then the resulting X is the desired solution, otherwise we go further. Thus, we obtain a decision tree, each branch of which is completed if on the sheet of this branch ceil (F2)> = F1_save, or if all the components from the basis are multiple k or if the task had no solution at all. The plan that corresponds to that obtained after building the F1_save tree is optimal.
PS Adding a restriction does not necessarily solve the problem again. You can, for example, sort through all possible F1-reducing cycles and select the optimal one among them. Or use the methods of the dual simplex method.
')
Example
Consider the algorithm on a very simple example. Let k = 3, C = {{2,2}, {4,5}}, a = {2,3}, b = {2,3}. So the top of the tree is the solution of such a transportation problem with the objective function F2:
0) X = {{0,2}, {2,1}}, F2 (X) ~ = 5.67, F1 (X) = 2 + 4 + 5 = 11.
F2_save: = 5.67, F1_save: = 11
because ceil (5.67) <11 go further - we build the next tier of the tree:
1.1) we add the condition x12 == 0 to the problem solved at node 0 and solve it again.
X = {{2.0}, {0.3}}, F2 (X) ~ = 6.35, F1 (X) = 2 + 5 = 7.
because F1 <F1_save (7 <11), then F1_save: = 7
because ceil (F2)> = F1_save (7> = 7), then we don’t continue this branch
because F1> ceil (F2_save) go further (perhaps there is a better solution), the branch does not continue, but the tier is not finished yet.
1.2) we add the condition x21 == 0 to the problem solved at node 0 and solve it again.
X = {{2.0}, {0.3}}, F2 (X) ~ = 6.35, F1 (X) = 2 + 5 = 7.
because F1 == F1_save (7 == 7), then F1_save does not change
because ceil (F2)> = F1_save (7> = 7), then we don’t continue this branch
because F1> ceil (F2_save) go further (perhaps there is a better solution), the branch does not continue, but the tier is not finished yet.
1.3) we add the condition x22 == 0 to the problem solved at node 0 and solve it again. Such a task has no solution => and we do not continue this branch.
There are no more basic components left (the tier is completed) and there is no need to continue the branches (meaningless, we will not get a better solution), so the tree has been built. F1_save == 7 is our minimum cost. Plan for them the corresponding (he is the answer) X = {{2,0}, {0,3}}
Source: https://habr.com/ru/post/208990/
All Articles