Pure functional data structures
I admit. I didn't really like the course on data structures and algorithms at the university. All these stacks, queues, heaps, trees, graphs (if they were not okay) and other “witty” names of incomprehensible and complex data structures didn’t want to be fixed in my head. As a true “pragmatist,” I already in the second - third year believed in a standard library of classes and prayed to collections (and mere mortals) bestowed on us and containers carefully realized by fathers and noble CS. It seemed that all that could be invented was already invented and implemented long ago.
Everything changed about a year ago, when I found out that there is another world. The world is different from ours with you. A cleaner and more predictable world. A world without side effects, mutations, arrays and destructive updates (reassignments to a variable). A world where the wise queen persistence rules and her beautiful sisters rule all - function and recursion. I'm talking about a purely functional world, where there are harmoniously, or even live, projections of almost all known data structures.
And now, I want to show you a small bit of this world. Through a keyhole, we look at this wonderful world for a second to consider one of its most striking inhabitants - the functional red-ebony (CCD).
Pure functional data structures (CFSDs) as a class exist for two reasons. First, for 99% imperative implementations, the stumbling block is the so-called destructive updates (assignment to a variable with the loss of the previous value). It is clear that such a scenario is impossible in the functional world, because we are always dealing with immutable objects. Secondly, in the functional world, after changing the collection, we expect that its previous version remains available to us. Hence the term “persistent object” (persistent object) - support for multiple versions of an object.
')
Thus, one cannot simply take and port a certain imperative realization into a functional world. It is necessary to remember about its limitations (no updates) and requirements (persistence). Therefore, the process of adapting an imperative implementation to a functional environment is somewhat more complex and even mysterious. And unsurpassed master in this difficult matter for 15 years, Chris Okasaki is considered with his fundamental work - Purely Functional Data Structures .
In 1998, Chris defended his thesis on CSDS and a year later published the theses in the form of a book. Chris's book is 200 pages of very dense (informative) and fascinating read. The text, whose style borders on scientific work and informal conversation with a friend in a bar, literally reads like an artistic novel. Chris's work combines the best practices and approaches in implementing CSFS, supported by examples of well-known (and not very) data structures in Standard ML and Haskell.
An attentive reader will say that with such requirements and restrictions everything will be terribly slow. It seems that any change in the functional collection is accompanied by its full copying in order to maintain persistence. This is not entirely true. More precisely - not at all. Copying is really present, but at the most minimal scale. More formally, only what really changes is copied. The rest of the collection (as a big plan) is shared between versions. These two sentences are the keys to understanding purely functional data structures. These are unique tools that are invented and honed by the sharpest minds of AF. The name of these tools is path copying (copying only what is affected in the operation) and structural sharing (common parts can be safely shared between versions, since each such part is itself unchangeable).
First, consider the usual unbalanced binary search trees (DBP), which are very easily ported to the functional world. Their structure looks like this:
We are interested in the insert operation, which will allow us to fully appreciate the strength and beauty of path copying and structural sharing tools.
As in the imperative algorithm, the problem of insertion is reduced to the problem of finding a suitable place for a new node. However, our functional implementation will be slightly more interesting. The insert operation into the functional tree combines two passes - a downward (top-down)
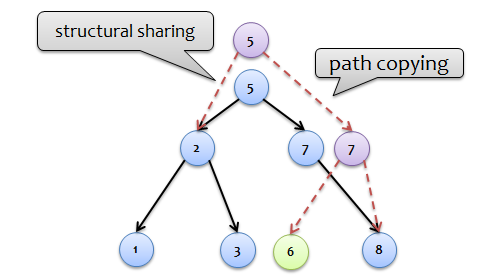
To preserve the persistence property, it is necessary to maintain two versions of the collection - “before” and “after” insertion. Therefore, any changes to the internal structure of the nodes should be made on their copies. As a result of inserting into a tree, a kind of “chain reaction” of updating nodes (changing links to the left / right descendant) occurs, extending along the search path from the insertion point to the root of the tree. This is the way to describe the “magic” that is implemented by the ascending passage, combining ideas and path copying (nodes “5” and “7” copied) and structural sharing (subtree with keys “1”, “2”, “3” contained in both versions of the collection).
A red-ebony tree (CCD) is a self-balancing binary search tree for which two invariants are valid:
Execution of these invariants ensures that the tree will be balanced with the height of log n, where n is the number of nodes in the tree. In other words, the main operations on the FDC are guaranteed to be performed in logarithmic time.
Until 1999, the KChD in the functional world was out of the question. The imperative implementation was notoriously difficult to port, since it was completely built on complex manipulations with pointers (pointers hell). For example, in Cormen, eight possible cases of violation of invariants and corresponding measures to eliminate them are considered. Slightly deviating from the topic, one can add that it is precisely because of the excessive complexity of the PSD that they tried in every possible way to replace with alternative things. For example, Sezhevik proposed the LLRB tree as a simplified version of the CHD.
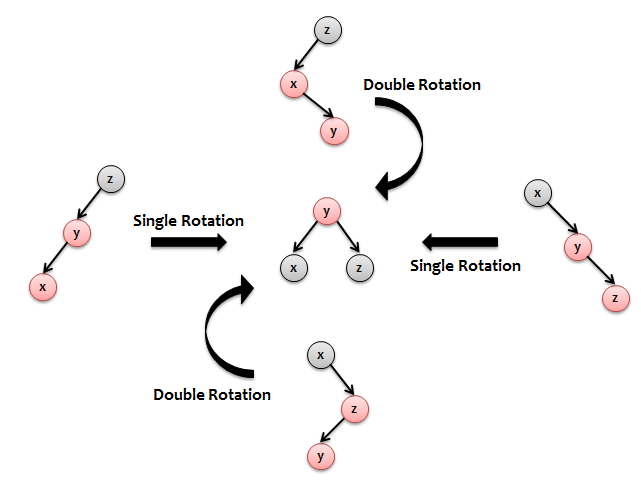
However, in 1999, Chris Okasaki published an article in which he presented a purely functional implementation of the PSD. This article is still in great demand among both functional programmers and imperative programmers. The fact is that the article presents a very simple and understandable idea of implementation, which any programmer can understand and program in 15 minutes. Chris said that there are only 4 patterns (see picture below) that break one of the invariants. And our task is to find these patterns and rebuild them into one and the same construction with a red root and two black children (see picture). And it's all. Those. in order to obtain a PSD from DBP, it is enough for us to change the second (ascending) pass of the insertion algorithm. Now the second pass should not just copy the nodes along the search path, but also if the subtree matches one of the four patterns, rebuild it into a safe structure. In other words, the copying phase in the algorithm is combined with the balancing phase.
Adding to this two simple facts that the CCD root is always black, and the new node is always red, we get the following code:
In the considered implementation, there are a couple more points that require additional comments. First, each tree node contains additional information — its own color (
A fair question arises - why the implementation of the CHD in the imperative world looks much more complicated? The answer is quite simple - to blame for performance. Dealing with pointers and variable variables, we can stop the balancing process at its earliest iterations (under certain conditions), thereby reducing the running time of the algorithm. In the functional environment, we are forced to copy all the affected nodes, so the extra checks for the presence of patterns in the subtrees do not bother us much. For the sake of justice, it is worth replacing that the proposed algorithm for inserting into a functional PSD has the same asymptotic complexity as the original algorithm from the imperative world - O (log n).
I have collected some great links for those interested in the topic.
For researchers:
For practitioners:
Everything changed about a year ago, when I found out that there is another world. The world is different from ours with you. A cleaner and more predictable world. A world without side effects, mutations, arrays and destructive updates (reassignments to a variable). A world where the wise queen persistence rules and her beautiful sisters rule all - function and recursion. I'm talking about a purely functional world, where there are harmoniously, or even live, projections of almost all known data structures.
And now, I want to show you a small bit of this world. Through a keyhole, we look at this wonderful world for a second to consider one of its most striking inhabitants - the functional red-ebony (CCD).
About purely functional data structures
Pure functional data structures (CFSDs) as a class exist for two reasons. First, for 99% imperative implementations, the stumbling block is the so-called destructive updates (assignment to a variable with the loss of the previous value). It is clear that such a scenario is impossible in the functional world, because we are always dealing with immutable objects. Secondly, in the functional world, after changing the collection, we expect that its previous version remains available to us. Hence the term “persistent object” (persistent object) - support for multiple versions of an object.
')
Thus, one cannot simply take and port a certain imperative realization into a functional world. It is necessary to remember about its limitations (no updates) and requirements (persistence). Therefore, the process of adapting an imperative implementation to a functional environment is somewhat more complex and even mysterious. And unsurpassed master in this difficult matter for 15 years, Chris Okasaki is considered with his fundamental work - Purely Functional Data Structures .
About Chris and his book
In 1998, Chris defended his thesis on CSDS and a year later published the theses in the form of a book. Chris's book is 200 pages of very dense (informative) and fascinating read. The text, whose style borders on scientific work and informal conversation with a friend in a bar, literally reads like an artistic novel. Chris's work combines the best practices and approaches in implementing CSFS, supported by examples of well-known (and not very) data structures in Standard ML and Haskell.
About two keys
An attentive reader will say that with such requirements and restrictions everything will be terribly slow. It seems that any change in the functional collection is accompanied by its full copying in order to maintain persistence. This is not entirely true. More precisely - not at all. Copying is really present, but at the most minimal scale. More formally, only what really changes is copied. The rest of the collection (as a big plan) is shared between versions. These two sentences are the keys to understanding purely functional data structures. These are unique tools that are invented and honed by the sharpest minds of AF. The name of these tools is path copying (copying only what is affected in the operation) and structural sharing (common parts can be safely shared between versions, since each such part is itself unchangeable).
About binary search trees
First, consider the usual unbalanced binary search trees (DBP), which are very easily ported to the functional world. Their structure looks like this:
abstract sealed class Tree { def value: Int def left: Tree def right: Tree def isEmpty: Boolean } case object Leaf extends Tree { def value: Int = fail("Empty tree.") def left: Tree = fail("Empty tree.") def right: Tree = fail("Empty tree.") def isEmpty: Boolean = true } case class Branch(value: Int, left: Tree = Leaf, right: Tree = Leaf) extends Tree { def isEmpty: Boolean = false } We are interested in the insert operation, which will allow us to fully appreciate the strength and beauty of path copying and structural sharing tools.
def add(x: Int): Tree = if (isEmpty) Branch(x) else if (x < value) Branch(value, left.add(x), right) else if (x > value) Branch(value, left, right.add(x)) else this As in the imperative algorithm, the problem of insertion is reduced to the problem of finding a suitable place for a new node. However, our functional implementation will be slightly more interesting. The insert operation into the functional tree combines two passes - a downward (top-down)
add call chain (searching for an insertion point) and a bottom-up call chain of the Branch constructor (copying a modified part of the tree along the search path). The first pass (the downward search for the insertion point) is an obvious projection of the imperative algorithm. We are also interested in the second pass (ascending path copying), which makes our implementation fully functional (persistent).
To preserve the persistence property, it is necessary to maintain two versions of the collection - “before” and “after” insertion. Therefore, any changes to the internal structure of the nodes should be made on their copies. As a result of inserting into a tree, a kind of “chain reaction” of updating nodes (changing links to the left / right descendant) occurs, extending along the search path from the insertion point to the root of the tree. This is the way to describe the “magic” that is implemented by the ascending passage, combining ideas and path copying (nodes “5” and “7” copied) and structural sharing (subtree with keys “1”, “2”, “3” contained in both versions of the collection).
About red and black trees
A red-ebony tree (CCD) is a self-balancing binary search tree for which two invariants are valid:
- Red invariant : no red node has a red ancestor
- Black invariant : each path from root to leaf has the same number of black nodes
Execution of these invariants ensures that the tree will be balanced with the height of log n, where n is the number of nodes in the tree. In other words, the main operations on the FDC are guaranteed to be performed in logarithmic time.
Until 1999, the KChD in the functional world was out of the question. The imperative implementation was notoriously difficult to port, since it was completely built on complex manipulations with pointers (pointers hell). For example, in Cormen, eight possible cases of violation of invariants and corresponding measures to eliminate them are considered. Slightly deviating from the topic, one can add that it is precisely because of the excessive complexity of the PSD that they tried in every possible way to replace with alternative things. For example, Sezhevik proposed the LLRB tree as a simplified version of the CHD.
However, in 1999, Chris Okasaki published an article in which he presented a purely functional implementation of the PSD. This article is still in great demand among both functional programmers and imperative programmers. The fact is that the article presents a very simple and understandable idea of implementation, which any programmer can understand and program in 15 minutes. Chris said that there are only 4 patterns (see picture below) that break one of the invariants. And our task is to find these patterns and rebuild them into one and the same construction with a red root and two black children (see picture). And it's all. Those. in order to obtain a PSD from DBP, it is enough for us to change the second (ascending) pass of the insertion algorithm. Now the second pass should not just copy the nodes along the search path, but also if the subtree matches one of the four patterns, rebuild it into a safe structure. In other words, the copying phase in the algorithm is combined with the balancing phase.

Adding to this two simple facts that the CCD root is always black, and the new node is always red, we get the following code:
def add(x: Int): Tree = { def balancedAdd(t: Tree): Tree = if (t.isEmpty) Tree.make(Red, x) else if (x < t.value) balanceLeft(t.color, t.value, balancedAdd(t.left), t.right) else if (x > t.value) balanceRight(t.color, t.value, t.left, balancedAdd(t.right)) else t def balanceLeft(c: Color, x: Int, l: Tree, r: Tree) = (c, l, r) match { case (Black, Branch(Red, y, Branch(Red, z, a, b), c), d) => Tree.make(Red, y, Tree.make(Black, z, a, b), Tree.make(Black, x, c, d)) case (Black, Branch(Red, z, a, Branch(Red, y, b, c)), d) => Tree.make(Red, y, Tree.make(Black, z, a, b), Tree.make(Black, x, c, d)) case _ => Tree.make(c, x, l, r) } def balanceRight(c: Color, x: A, l: Tree, r: Tree) = (c, l, r) match { case (Black, a, Branch(Red, y, b, Branch(Red, z, c, d))) => Tree.make(Red, y, Tree.make(Black, x, a, b), Tree.make(Black, z, c, d)) case (Black, a, Branch(Red, z, Branch(Red, y, b, c), d)) => Tree.make(Red, y, Tree.make(Black, x, a, b), Tree.make(Black, z, c, d)) case _ => Tree.make(c, x, l, r) } def blacken(t: Tree) = Tree.make(Black, t.value, t.left, t.right) blacken(balancedAdd(this)) } In the considered implementation, there are a couple more points that require additional comments. First, each tree node contains additional information — its own color (
color function). Secondly, the balance function, which implements balancing and copying, is divided into two functions (the balanceLeft and balanceRight ), which expect to find violation of invariants in the left or right subtree (only along the search patch), and process two patterns for each side, respectively.On the complexity of imperative implementation
A fair question arises - why the implementation of the CHD in the imperative world looks much more complicated? The answer is quite simple - to blame for performance. Dealing with pointers and variable variables, we can stop the balancing process at its earliest iterations (under certain conditions), thereby reducing the running time of the algorithm. In the functional environment, we are forced to copy all the affected nodes, so the extra checks for the presence of patterns in the subtrees do not bother us much. For the sake of justice, it is worth replacing that the proposed algorithm for inserting into a functional PSD has the same asymptotic complexity as the original algorithm from the imperative world - O (log n).
About further steps
I have collected some great links for those interested in the topic.
For researchers:
- My review presentation of ChFSD with examples on Scala (video report for the Novosibirsk Scala meeting here )
- My attempt to port a binary heap to the functional world
- Code of PSD and other structures on GitHub
- Removal from PSD from Metta Mait
- Chris Okasaki's blog
For practitioners:
- Anre Andersonin in this article proposed to reduce the number of comparisons from “2 * d” to “d + 1”, where d is the depth of the tree (search path length). Modify the insert operation in DBP so that it uses fewer comparisons.
- Write a function
fromOrderedList, which builds a balanced DBP from a sorted list. Hint: Hinze, Ralf. 1999 "Constructing red-black trees".
Source: https://habr.com/ru/post/208918/
All Articles