Why do we all need SAT and all these P-NPs (part two)
The previous part covered publicly available questions concerning SAT and P-NP: problem history, intuitive definitions of classes and tasks, basic SAT applications and main consequences, in cases of solving P? = NP (there you can also find a sufficient number of references to various materials for self-study topics).
In this article we will look at the technical side of the question, as well as formalize and present in detail the material from the previous article.
')
Picture from article Boolean Satisfiability: From Theoretical Hardness to Practical Success (Communications of ACM)
For ease of reading and navigation provide a brief overview of the contents of the article.
In the previous work, only the simplest solution scenario was considered, which caused a number of interesting remarks (the author is grateful for interesting and useful links on this issue). In this article, we will consider all sorts of options and their consequences, taking into account comments and observations to previous work.
Here, quite interestingly from an artistic point of view, the discussion is described around various solutions.
There are several options for the development of the situation.
As in the previous case, the decision can be constructive and non-constructive. Consider the constructive case (non-constructive in structure is similar to the previous case)
Detailed and interesting about this is written in the article Is P Versus NP Formally Independent? by Scott Aaronson (the article requires sufficient mathematical culture to understand; approximate reading time is ~ 1/2 pm). We give a brief overview of the contents of the article.
The main message of the article in the following may turn out to be that both the hypotheses P = NP and P! = NP are consistent with the theory of sets. This can happen if P vs. NP is independent of the axiomatics of set theory, as for example, the axiom of choice is independent of the other axioms of set theory. From a practical point of view, this would mean that P! = NP.
In the theory of complexity, it is customary to formulate problems in the form of “solvability problems” i. tasks, the answer to which can only be "yes" or "no." Classes P and NP are formally defined in terms of languages and Turing machines.
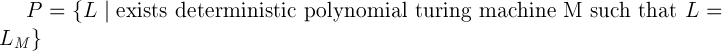
where L M is the language taken by machine M.
We say that a particular problem p belongs to the class P if there is a deterministic Turing machine that takes the language L (p) for a polynomial number of steps.
With the NP class, everything is a little more interesting, this is a class of problems where the correctness of the solution can be checked in polynomial time. Formally, we say that the language L belongs to NP, if and only if, there exists a deterministic Turing machine M, such that for any string x is true:

where | y | - is bounded by a polynomial and M makes a polynomial number of steps. For "y" there is a special term - certificate. In fact, the definition is read as follows - the task belongs to NP, if there exists a polynomial solution, the correctness of which can be checked in polynomial time. Note that this definition is asymmetric with respect to the question when the language is NOT NP, that is, The question is not whether the NP language is a separate class.
What kind of class is Co-NP? Co-NP is complement NP, intuitively, this is a class, the tasks in which are the negation of tasks in NP. If the SAT asks if the assignment is true / false for the variables that the formula is correct, then UNSAT asks if it is true that for ALL assignments the formula is incorrect? Those. in other words, is it true that the certificate does not exist.
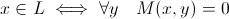
or in another way it can be formulated as follows:
NP is a collection of languages with short certificates confirming membership.
Co-NP is a collection of languages with concise certificates rejecting membership (= there is no membership certificate)
If NP! = Co-NP, then the set of NP-complete and Co-NP-complete tasks do not intersect (a consequence of Mahaney's theorem ).
More information about languages, Turing machines and definitions of complexity classes can be found in M. Gary, D. Johnson: Computers and intractable problems (for example, here )
According to modern concepts, the relationship between NP, Co-NP and P is as follows:
(picture taken from here )
Most are inclined to option (d), but some believe that other options are likely to be possible, eg The Whip in The Art of Programming 4, 6A draft: Satisfibility - page 1, footnote (*): "... the author of this book, however, suspects that polynomial algorithms [for SAT - author's note] really exist, only they are not yet known to us ... ".
In a previous article, it was shown that 2-SAT is polynomial, i.e. if we limit each clause to two variables, the problem can be solved effectively. Consider a natural generalization of this problem, what if we have only part of the sentences contains 3 variables?
Let p be the number of sentences with 3 variables to the total number of sentences. Then the 2 + p SAT task is a 3-SAT problem, in which the number of sentences with 3 variables, i.e. p, respectively (1 - p) sentences have 1 or 2 variables.
From a theoretical point of view, even if p is the concentration of a barbarian duck in an ocillococcinum, i.e. any positive number, the NP problem is complete, but in practice it looks completely different.
Let the X axis be the total number of variables in a formula, the Y axis the “computational cost” of a solution for a given formula (usually the number of calls / solutions of the state-of-the-art SAT-solver algorithm, see the brief description of DPLL and CDCL in previous article).
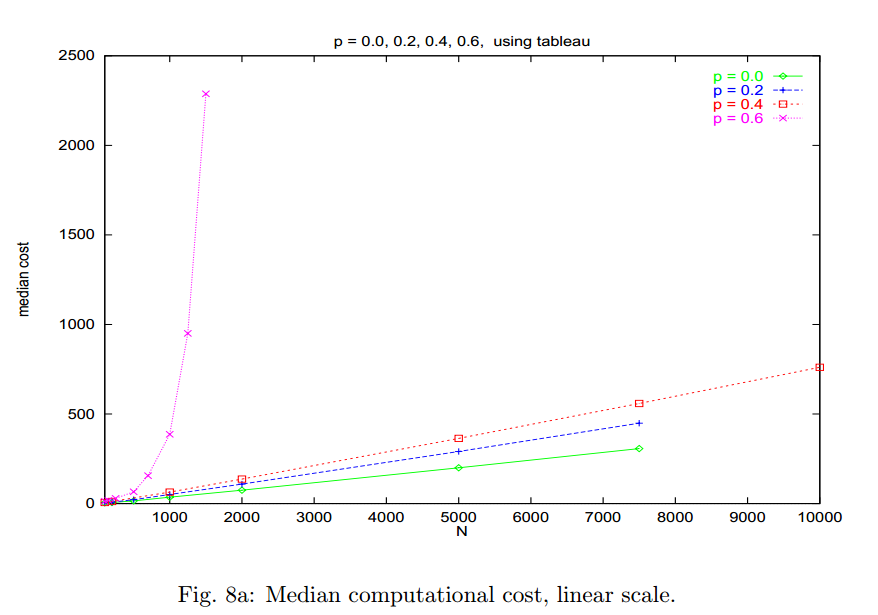
(Schedule taken from work 2 + P-SAT: Relation of typical phase transition ).
If p <= 0.4, then the problem is polynomial, even more so, linear in the input data. If p> 0.4, then we observe behavior similar to the classic 3-SAT. To explain this effect, consider the classic DPLL algorithm (taken from Armin Biere slides):

Consider a simple example.
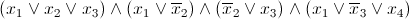
Let the algorithm, chose x 2 = 1
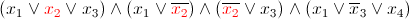
Then the formula is simplified and we have two sentences with a single variable - it means that boolean constraint propagation selects one of them, for example, x 3 and assigns the only value available to it
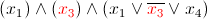
after assignment x 3 = 1, BCP again finds a sentence with a single variable x 1 , and assigns x 1 = 1
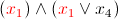
Thus, after a single SAT solver solution, boolean constraint propagation allows finding a solution to the entire formula. This happens primarily because the decision on a variable in a two-variable sentence actually uniquely determines the value of another variable, which causes a whole cascade of assignments and the BCP effectively reduces the formula. If such a cascade covers a sufficient number of variables in a formula, then the solution is linear.
Another interesting relationship is the so-called clause-variable-ratio: the ratio of the number of sentences to the number of variables. Intuitively, the more sentences, the more restrictions, the more likely that formulas are impracticable - too many restrictions. They say that such a problem is overconstrained. If there are few sentences and many variables, it means that there are many degrees of freedom and few restrictions. This makes it easy to find a solution, and it is likely that the formula is workable. They say about her that she is underconstrained.
Since we have already considered 2 + p SAT, it would also be interesting to take into account the parameter p in this relationship, as the degree of "linearity" of the problem, the greater the p, the less effective boolean constraint propagation and the more difficult it is to find a solution.
SAT / UNSAT transition for 2 + p SAT
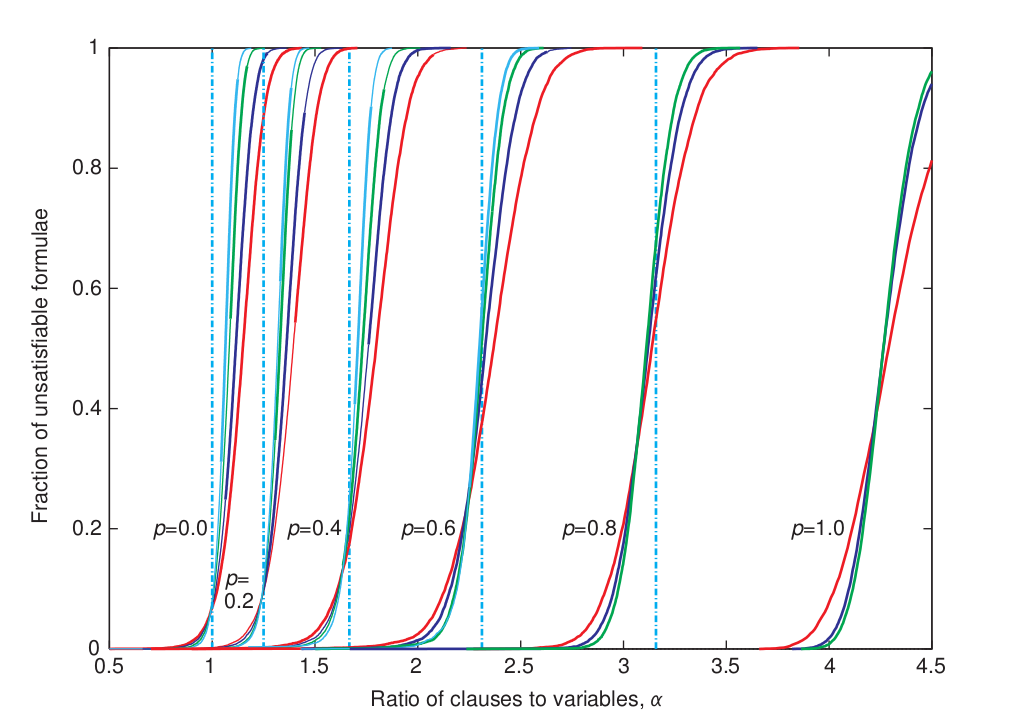
Graph from Nature article: Determining computational complexity from characteristic `phase transitions' by Remi Monasson, Riccardo Zecchina, Scott Kirkpatrick, Bart Selman and Lidror Troyanskyk
In fact, this graph gives us more than we think: it allows us to generate "complex" random formulas. If the formula is somewhere in the center between SAT and UNSAT, this means that it is difficult for her to find a model and it is difficult to generate proof of impracticability.
The dependence of the number of DPLL calls on the position of the SAT / UNSAT transition is as follows
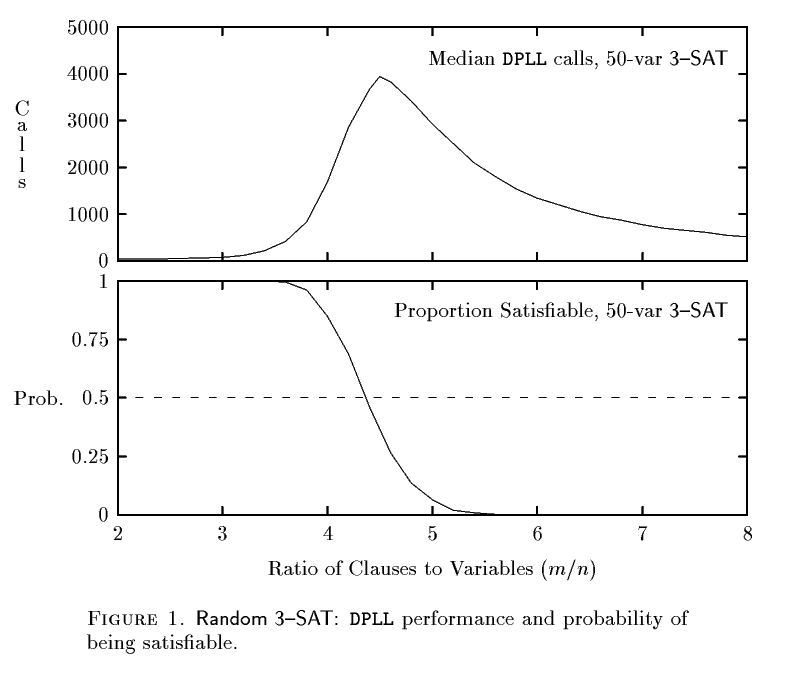
Graph from the article Finding Hard Instances of the Satisability ability Problem: A Survey by S. Cook, D. Mitchell
Even a description of the basic principles, algorithms and heuristics will take more than one hundred pages, so we confine ourselves to one of the descriptions of one of the most popular and key SAT algorithms: CDCL - Conflict Driven Clause Learning. As the name suggests, one of the main features of this algorithm is the ability to memorize solutions that do not lead to a solution, namely, the algorithm remembers them in the form of sentences. If we make decisions x 1 = 1, x 2 = 2, x 3 = 1 and this leads to a conflict, then CDCL will remember the negation of the conflicting combination.
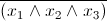
according to De Morgan's rule, we bring to CNF
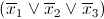
and add it to the formula

Thus, there are two key components of CDCL: an implication graph with a stack of decisions taken and work with conflicting combinations. As a rule, after making a decision, the algorithm performs all possible deterministic calculations and comes to a conflict. The graph of implications and the solution stack show what combination and decision at which stage led to a conflict, based on this, generating a conflict proposal - hence the name Conflict Driven Clause Learning, the algorithm effectively finds conflict combinations, learns them and makes decisions, considering conflict combinations .
Consider the example of the work of the CDCL algorithm in more detail:
from Masahiro Sakai
More about CDCL is written in the following papers:
Handbook of Satisfaction ability: Chapter 4. Conversing Driving Sailors by Joao Marques-Silva, Ines Lynce and Sharad Malik
SAT / SMT Summer School 2013 author slides CDCL: CDCL SAT Solvers & SAT-Based Problem Solving
Detailed and sufficient technical description of the operation of the algorithm and internal structures: Practical SAT Solving: Con fl ict-driven SAT solvers
First, you need to answer a series of questions for compliance with a common sense decision.
Assume that all these conditions are met, then the second, what will be considered a recognized solution? Publication in the journal "Automation and Mechanics" ? There are several conferences suitable for the P vs NP problem:
STOC, the Annual ACM Symposium on Theory of Computing
TAGL, ACM Transactions on Algorithms
FOCS, The IEEE Annual Symposium on Foundations of Computer Science
If they (any of these conferences) recognize your decision, you can safely count on your million - until this point the decision is considered one of the many wrong decisions P vs. Np.
An interesting roadmap (more precisely, even an interactive list of questions) on the issue of checking P vs. NP solutions are presented here .
If you give a short answer, it is because the article does not answer any of the questions from the list of "common sense":
Further, let us assume that the work will be corrected, then it still does not make sense to write open letters to anyone - modern science does not work that way, it is your task to convince the public that the solution is correct. This can be done only through the prism of expert opinion, see the conference described above.
Usually, everything is explained well and well in SAT / SMT summer schools:
school materials 2013
school materials 2012
Soon there will be a fresh whip about SAT - a draft is available: The Art of Programming 4, 6A: Satisfibility
A large number of links is present in the previous post. Why do we all need SAT and all these P-NPs (part one)
Key here:
about SAT-solvers:
SAT Solvers: A Condensed History
Understanding Modern SAT Solvers - by Armin Biere, perhaps the most famous developer of SAT Solvers in the world. Donald Knut, who is now writing “The Art of Computer Programming: Volume 4B, Pre-fascicle 6A Satisfiability,” says he is consulting with him on many issues.
Towards SAT Solvers
about NP history:
The Question of Michael Sipser
P versus NP by Elvira Mayordomo
One of the most famous and respected works on the theory of complexity:
Gary M., Johnson D. - Computers and inaccessible tasks [1982]
Discrepancies of SAT, relational algebra, and stop problems.
Three statements are given:
1. First-order logic and relational algebra have the same “computational complexity,” that is, if a problem has complexity X in one formalism, then there is its expression in another formalism with the same complexity ( link ).
2. Relational algebra is not capable of expressing a transitive closure - a problem in the class P ( relational algebra: transitive closure )
3. SAT for first-order logic is equivalent to the stop problem and is algorithmically unsolvable ( link ).
Question: How can this be?
In this article we will look at the technical side of the question, as well as formalize and present in detail the material from the previous article.

')
Picture from article Boolean Satisfiability: From Theoretical Hardness to Practical Success (Communications of ACM)
Article structure
For ease of reading and navigation provide a brief overview of the contents of the article.
- Generally available material ( first part )
- Why is SAT important to all of us? Applications / Interesting NP tasks and SAT
- The history of SAT and NP-completeness
- "Intuitive Definition" SAT, NP and P
- What happens if ... P! = NP, P = NP
- 2-SAT polynomial: algorithm and intuition
- A challenge to think about
- Specialized material (this article)
- What happens if ... (in detail)
- Formal definition. Asymmetry of the solvability problem for NP. CoNP class.
- 2 + p-SAT polynomial?
- The dependence of the complexity of the number of variables
- About modern SAT solvers
- I decided to P vs. NP, what should I do? Where should i write?
- Inexpressibility theorems: why the article by Romanov expects a reject
- What to read?
- A challenge to think about
What if…
In the previous work, only the simplest solution scenario was considered, which caused a number of interesting remarks (the author is grateful for interesting and useful links on this issue). In this article, we will consider all sorts of options and their consequences, taking into account comments and observations to previous work.
Here, quite interestingly from an artistic point of view, the discussion is described around various solutions.
P = NP
There are several options for the development of the situation.
- Constructive solution
- The polynom has a low degree and moderate coefficients: then the details are described in the P = NP part of the previous article ; in short: all cryptography will collapse
- Polynomial has a high degree - then nothing will change from a practical point of view. P! = NP
- Non-constructive solution
- If we are unable to obtain an algorithm from this proof, then from a practical point of view, P! = NP
- If we can, then the question P? = NP, is transformed into a question of time and the creation of an algorithm from the proof
P! = NP
As in the previous case, the decision can be constructive and non-constructive. Consider the constructive case (non-constructive in structure is similar to the previous case)
- The complexity of the solution is always exponential: no changes, the current picture of the world will be fully preserved, no changes in algorithms
- The complexity of the solution is non-always exponential (see this post ), and for a sufficient number of cases it is polynomial. In this case, it is almost impossible to predict unambiguously what will happen and you can only speculate: if the factorization task falls into the “class of easy problems”, then from a practical point of view this will be equivalent to P = NP for an attack on RSA.
- The complexity of the solution is moderate or low (eg n log (n) ), in this case from a practical point of view it will be equivalent to P = NP
P vs. NP is not soluble in ZFC axiomatics
Detailed and interesting about this is written in the article Is P Versus NP Formally Independent? by Scott Aaronson (the article requires sufficient mathematical culture to understand; approximate reading time is ~ 1/2 pm). We give a brief overview of the contents of the article.
The main message of the article in the following may turn out to be that both the hypotheses P = NP and P! = NP are consistent with the theory of sets. This can happen if P vs. NP is independent of the axiomatics of set theory, as for example, the axiom of choice is independent of the other axioms of set theory. From a practical point of view, this would mean that P! = NP.
Formal definition. Asymmetry of the solvability problem for NP. CoNP class.
In the theory of complexity, it is customary to formulate problems in the form of “solvability problems” i. tasks, the answer to which can only be "yes" or "no." Classes P and NP are formally defined in terms of languages and Turing machines.
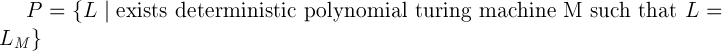
where L M is the language taken by machine M.
We say that a particular problem p belongs to the class P if there is a deterministic Turing machine that takes the language L (p) for a polynomial number of steps.
With the NP class, everything is a little more interesting, this is a class of problems where the correctness of the solution can be checked in polynomial time. Formally, we say that the language L belongs to NP, if and only if, there exists a deterministic Turing machine M, such that for any string x is true:

where | y | - is bounded by a polynomial and M makes a polynomial number of steps. For "y" there is a special term - certificate. In fact, the definition is read as follows - the task belongs to NP, if there exists a polynomial solution, the correctness of which can be checked in polynomial time. Note that this definition is asymmetric with respect to the question when the language is NOT NP, that is, The question is not whether the NP language is a separate class.
What kind of class is Co-NP? Co-NP is complement NP, intuitively, this is a class, the tasks in which are the negation of tasks in NP. If the SAT asks if the assignment is true / false for the variables that the formula is correct, then UNSAT asks if it is true that for ALL assignments the formula is incorrect? Those. in other words, is it true that the certificate does not exist.
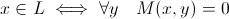
or in another way it can be formulated as follows:
NP is a collection of languages with short certificates confirming membership.
Co-NP is a collection of languages with concise certificates rejecting membership (= there is no membership certificate)
If NP! = Co-NP, then the set of NP-complete and Co-NP-complete tasks do not intersect (a consequence of Mahaney's theorem ).
More information about languages, Turing machines and definitions of complexity classes can be found in M. Gary, D. Johnson: Computers and intractable problems (for example, here )
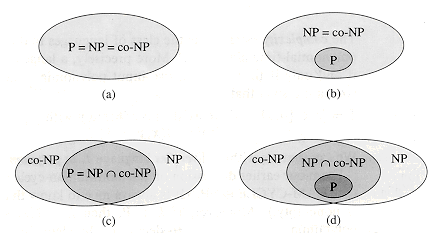
According to modern concepts, the relationship between NP, Co-NP and P is as follows:

(picture taken from here )
Most are inclined to option (d), but some believe that other options are likely to be possible, eg The Whip in The Art of Programming 4, 6A draft: Satisfibility - page 1, footnote (*): "... the author of this book, however, suspects that polynomial algorithms [for SAT - author's note] really exist, only they are not yet known to us ... ".
2 + p-SAT polynomial?
In a previous article, it was shown that 2-SAT is polynomial, i.e. if we limit each clause to two variables, the problem can be solved effectively. Consider a natural generalization of this problem, what if we have only part of the sentences contains 3 variables?
Let p be the number of sentences with 3 variables to the total number of sentences. Then the 2 + p SAT task is a 3-SAT problem, in which the number of sentences with 3 variables, i.e. p, respectively (1 - p) sentences have 1 or 2 variables.
From a theoretical point of view, even if p is the concentration of a barbarian duck in an ocillococcinum, i.e. any positive number, the NP problem is complete, but in practice it looks completely different.
Let the X axis be the total number of variables in a formula, the Y axis the “computational cost” of a solution for a given formula (usually the number of calls / solutions of the state-of-the-art SAT-solver algorithm, see the brief description of DPLL and CDCL in previous article).

(Schedule taken from work 2 + P-SAT: Relation of typical phase transition ).
If p <= 0.4, then the problem is polynomial, even more so, linear in the input data. If p> 0.4, then we observe behavior similar to the classic 3-SAT. To explain this effect, consider the classic DPLL algorithm (taken from Armin Biere slides):

Consider a simple example.
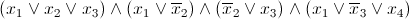
Let the algorithm, chose x 2 = 1
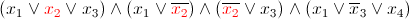
Then the formula is simplified and we have two sentences with a single variable - it means that boolean constraint propagation selects one of them, for example, x 3 and assigns the only value available to it
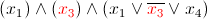
after assignment x 3 = 1, BCP again finds a sentence with a single variable x 1 , and assigns x 1 = 1
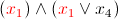
Thus, after a single SAT solver solution, boolean constraint propagation allows finding a solution to the entire formula. This happens primarily because the decision on a variable in a two-variable sentence actually uniquely determines the value of another variable, which causes a whole cascade of assignments and the BCP effectively reduces the formula. If such a cascade covers a sufficient number of variables in a formula, then the solution is linear.
The dependence of the complexity of the number of variables
Another interesting relationship is the so-called clause-variable-ratio: the ratio of the number of sentences to the number of variables. Intuitively, the more sentences, the more restrictions, the more likely that formulas are impracticable - too many restrictions. They say that such a problem is overconstrained. If there are few sentences and many variables, it means that there are many degrees of freedom and few restrictions. This makes it easy to find a solution, and it is likely that the formula is workable. They say about her that she is underconstrained.
Since we have already considered 2 + p SAT, it would also be interesting to take into account the parameter p in this relationship, as the degree of "linearity" of the problem, the greater the p, the less effective boolean constraint propagation and the more difficult it is to find a solution.
SAT / UNSAT transition for 2 + p SAT

Graph from Nature article: Determining computational complexity from characteristic `phase transitions' by Remi Monasson, Riccardo Zecchina, Scott Kirkpatrick, Bart Selman and Lidror Troyanskyk
In fact, this graph gives us more than we think: it allows us to generate "complex" random formulas. If the formula is somewhere in the center between SAT and UNSAT, this means that it is difficult for her to find a model and it is difficult to generate proof of impracticability.
The dependence of the number of DPLL calls on the position of the SAT / UNSAT transition is as follows

Graph from the article Finding Hard Instances of the Satisability ability Problem: A Survey by S. Cook, D. Mitchell
About modern SAT solvers
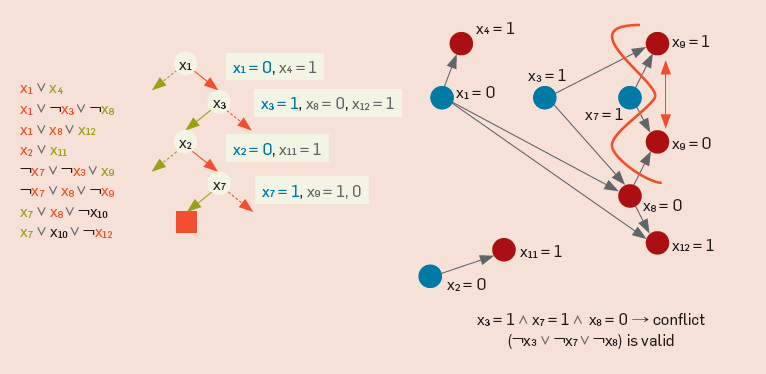
Even a description of the basic principles, algorithms and heuristics will take more than one hundred pages, so we confine ourselves to one of the descriptions of one of the most popular and key SAT algorithms: CDCL - Conflict Driven Clause Learning. As the name suggests, one of the main features of this algorithm is the ability to memorize solutions that do not lead to a solution, namely, the algorithm remembers them in the form of sentences. If we make decisions x 1 = 1, x 2 = 2, x 3 = 1 and this leads to a conflict, then CDCL will remember the negation of the conflicting combination.
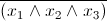
according to De Morgan's rule, we bring to CNF
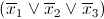
and add it to the formula

Thus, there are two key components of CDCL: an implication graph with a stack of decisions taken and work with conflicting combinations. As a rule, after making a decision, the algorithm performs all possible deterministic calculations and comes to a conflict. The graph of implications and the solution stack show what combination and decision at which stage led to a conflict, based on this, generating a conflict proposal - hence the name Conflict Driven Clause Learning, the algorithm effectively finds conflict combinations, learns them and makes decisions, considering conflict combinations .
Consider the example of the work of the CDCL algorithm in more detail:
from Masahiro Sakai
More about CDCL is written in the following papers:
Handbook of Satisfaction ability: Chapter 4. Conversing Driving Sailors by Joao Marques-Silva, Ines Lynce and Sharad Malik
SAT / SMT Summer School 2013 author slides CDCL: CDCL SAT Solvers & SAT-Based Problem Solving
Detailed and sufficient technical description of the operation of the algorithm and internal structures: Practical SAT Solving: Con fl ict-driven SAT solvers
I decided to P vs. NP, what should I do? Where should i write?
First, you need to answer a series of questions for compliance with a common sense decision.
- Can the work explain why other attempts to solve the problem have failed, and our work is not
- How this work circumvents the ineffability theorem explicitly show that these theorems (eg Baker-Gill-Solovay theorem) are not applicable to this work.
- If P = NP and the proof is constructive, then a prototype is obligatory, otherwise no one will believe in the solution.
- The work is self-sufficient and available to the expert for understanding. it contains all the necessary definitions, proofs in expanded form (the millennium task, written on 3 pages with hieroglyphs and inaccessible language, arouses suspicion and the desire of the inspector to poison her into the basket)
- The authors have a good understanding of the theory of complexity, ie they are familiar with all the major works and works and know what happened in this scientific field in recent years.
Assume that all these conditions are met, then the second, what will be considered a recognized solution? Publication in the journal "Automation and Mechanics" ? There are several conferences suitable for the P vs NP problem:
STOC, the Annual ACM Symposium on Theory of Computing
TAGL, ACM Transactions on Algorithms
FOCS, The IEEE Annual Symposium on Foundations of Computer Science
If they (any of these conferences) recognize your decision, you can safely count on your million - until this point the decision is considered one of the many wrong decisions P vs. Np.
An interesting roadmap (more precisely, even an interactive list of questions) on the issue of checking P vs. NP solutions are presented here .
Why article Romanov expects reject
If you give a short answer, it is because the article does not answer any of the questions from the list of "common sense":
- The article does not contain “related work” at all, it seems that for 40 years in the theory of complexity there was no progress at all (the author only referred to himself three times): for example, you can take a look at The NP-Completeness Column: David S. Johnson , briefly briefly on the case talks about all the related work, the normal quality work in TAGL
- This work allows an algebraic representation (plates of variables, a graph on these plates, and a slightly conjunctive query for checking properties) —Aaronson-Wigderson theorem (generalizing the Baker-Gill-Solovay theorem) on the undecidability of Ps can be directly applied. NP using algebraic methods. By the way, if inspectors have a doubt that you ignore such results intentionally, this will be interpreted against the submitted work.
- Where is the prototype not running away to the exponent in the asymptotics?
- Where is the pseudocode algorithm? Where is a full-fledged working example: the input data is a well-known complex example, the operation of the algorithm and the output data are shown step by step? Where is the formalization? in the article on 17 pages, two formulas of the form (a => b) and informal phrases in the spirit: "grouping the lines of
- There are no key references in the work, for example, on the work of Levin-Cook.
Further, let us assume that the work will be corrected, then it still does not make sense to write open letters to anyone - modern science does not work that way, it is your task to convince the public that the solution is correct. This can be done only through the prism of expert opinion, see the conference described above.
What to read?
Usually, everything is explained well and well in SAT / SMT summer schools:
school materials 2013
school materials 2012
Soon there will be a fresh whip about SAT - a draft is available: The Art of Programming 4, 6A: Satisfibility
A large number of links is present in the previous post. Why do we all need SAT and all these P-NPs (part one)
Key here:
about SAT-solvers:
SAT Solvers: A Condensed History
Understanding Modern SAT Solvers - by Armin Biere, perhaps the most famous developer of SAT Solvers in the world. Donald Knut, who is now writing “The Art of Computer Programming: Volume 4B, Pre-fascicle 6A Satisfiability,” says he is consulting with him on many issues.
Towards SAT Solvers
about NP history:
The Question of Michael Sipser
P versus NP by Elvira Mayordomo
One of the most famous and respected works on the theory of complexity:
Gary M., Johnson D. - Computers and inaccessible tasks [1982]
A challenge to think about
Discrepancies of SAT, relational algebra, and stop problems.
Three statements are given:
1. First-order logic and relational algebra have the same “computational complexity,” that is, if a problem has complexity X in one formalism, then there is its expression in another formalism with the same complexity ( link ).
2. Relational algebra is not capable of expressing a transitive closure - a problem in the class P ( relational algebra: transitive closure )
3. SAT for first-order logic is equivalent to the stop problem and is algorithmically unsolvable ( link ).
Question: How can this be?
Source: https://habr.com/ru/post/208774/
All Articles