Depreciation analysis
Hi, Habr!
Today we talk about depreciation analysis. First, I will tell you what it is and give a toy example. And then I will tell you how to use it for analyzing a system of disjoint sets.
Depreciation analysis is used for algorithms that run several times. The algorithm time can vary greatly, but we estimate the average or total time for all runs. Most often, the algorithm implements some operation on the data structure.
')
The word "depreciation" came from finance. It means small periodic payments to repay the loan. In the lower case, it means that fast operations compensate for their costs for slow operations.
Consider the sequence of operations . Every operation
. Every operation  in fact performed in time
in fact performed in time 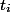 . This time is called actual. For each operation
. This time is called actual. For each operation  we calculate the amortization time
we calculate the amortization time 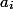 . We enter this time to make it easier to evaluate.
. We enter this time to make it easier to evaluate. 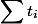 . From here two restrictions follow: a) formal - for any moment
. From here two restrictions follow: a) formal - for any moment 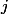 inequality holds
inequality holds 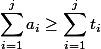 , and b) informal - the sum of depreciation values should be easily considered.
, and b) informal - the sum of depreciation values should be easily considered.
To have a concrete example in front of us, consider the data structure, inside which the stack lies. The data structure supports the elements and then inserts the element
elements and then inserts the element  .
.
We will assume that the arguments are always correct, and they will never ask us to throw out more than what is on the stack. In addition, we assume that step without
step without  -notations All our estimates can always be multiplied by a constant to get correct.
-notations All our estimates can always be multiplied by a constant to get correct.
Note that the time operation steps. A rough estimate will give time
steps. A rough estimate will give time 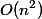 to fulfill all
to fulfill all  operations.
operations.
Depreciation analysis offers three valuation methods.
Let every unit of time is a coin. We will issue each operation coins and allow to spend
coins and allow to spend 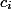 . All your coins transactions can be decomposed by data structure. The depreciation value of one operation will be
. All your coins transactions can be decomposed by data structure. The depreciation value of one operation will be 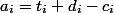 .
.
To maintain the invariant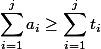 , we will set a restriction: you cannot spend more coins than there are at the moment:
, we will set a restriction: you cannot spend more coins than there are at the moment: 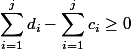 . Insofar as
. Insofar as  then
then 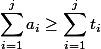 .
.
For our example, we will issue one coin to each operation (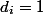 ). Put it on the element that we just added to the stack. So we paid for the future POP of this item.
). Put it on the element that we just added to the stack. So we paid for the future POP of this item.
Note that at any time point on each element of the stack lies on the coin, i.e. All POPs are prepaid.
To throw out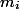 items we spend all the coins that lie on them (
items we spend all the coins that lie on them ( 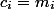 ). Then the depreciation value of each operation
). Then the depreciation value of each operation 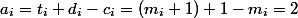 . It remains to be noted that
. It remains to be noted that  . We got the top linear score for execution
. We got the top linear score for execution  operations.
operations.
Any data structure can take several possible states. Let be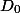 Is its initial state before all operations, and
Is its initial state before all operations, and 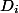 - state after
- state after  -th operation. We will introduce the potential function
-th operation. We will introduce the potential function 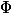 which takes as input the current state of the data structure and returns some non-negative number. Potential
which takes as input the current state of the data structure and returns some non-negative number. Potential 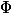 The initial state must be zero. For simplicity, we denote
The initial state must be zero. For simplicity, we denote 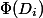 through
through 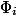 , but
, but 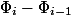 through
through 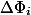 . Depreciation value
. Depreciation value 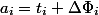 .
.
Invariant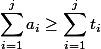 follows from the definition of potential. Really,
follows from the definition of potential. Really, 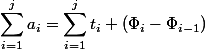 ; everything
; everything 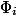 , except the first and last, are reduced and
, except the first and last, are reduced and  . Insofar as
. Insofar as 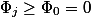 then
then 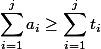 .
.
The general idea is to find such a potential function, which would have fallen heavily on expensive operations, compensating for the actual time, but on cheap ones it would grow a little. For our example, the number of items in the stack is appropriate. After
 . Then the depreciation value
. Then the depreciation value 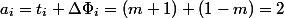 , and again we obtain a linear estimate.
, and again we obtain a linear estimate.
This method is a generalization of the previous two, and is to somehow count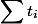 and divide by the number of requests.
and divide by the number of requests.
In our case, this reasoning works. Each elements, throw out no more
elements, throw out no more  . So, the total time is
. So, the total time is  . Amortization value of a single operation
. Amortization value of a single operation  .
.
We were given items. Elements can be combined into sets. We want to make a data structure that supports three operations.
items. Elements can be combined into sets. We want to make a data structure that supports three operations.
The data structure that supports these operations is called the disjoint-set (SNM) system (English disjoint-set data structure, union-find data structure or merge-find set).
On Habré already wrote about SNM. A detailed description of the algorithm and its application can be found here . In this post, I briefly recall the algorithm itself and concentrate on the analysis.
Each set we will store as a tree. The tree node stores a reference to the parent. If the node is a root, the link points to
To handle sets, we will select a representative for each set. In our case, this will be the root of the tree. If for two elements the representative matches, then they lie in one set. To combine two sets, you need to hang one tree to the root of another. We get a simple algorithm:
To speed up the algorithm, two heuristics are used.
Ranks . Each node is assigned a rank, initially equal to zero. The rank of the tree is the rank of its root. When combining sets, we will hang a tree of lower rank to a larger tree. If the ranks match, then first increase the rank of one of the trees by one.
Only one rank heuristic is enough to speed up the work of the SNM to for surgery at worst. But we will go further.
for surgery at worst. But we will go further.
Compression paths . Let we run . You may notice that all the vertices on the way from
. You may notice that all the vertices on the way from  until the root can be hung directly to the root.
until the root can be hung directly to the root.

Surprisingly, together these two heuristics reduce the depreciation time of a single operation to almost a constant.
In 1973, Hopcroft and Ullman showed that SNM with two heuristics processes operations for
operations for 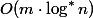 where
where  - iterative logarithm. Later, in 1975, Taryan showed that the SNM was working for
- iterative logarithm. Later, in 1975, Taryan showed that the SNM was working for 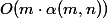 where
where  - the inverse function of Ackermann.
- the inverse function of Ackermann.
My plan is to first analyze what kind of cunning functions are, then to prove a simple logarithmic estimate in the worst case, and at the end to analyze the estimate of Hopkroft and Ulman. Tarjan's assessment is also actively using depreciation analysis, but contains more technical details.
Iterative logarithm is the function inverse to a power tower. Let's imagine the number of the form where only twos will be
where only twos will be  . Then
. Then  - this is the minimum
- this is the minimum  that power tower height
that power tower height  there will be more
there will be more  . Formally
. Formally
Exercise the reader to show that the iterative logarithm of the number of particles in the known part of the universe does not exceed five.
One might think that the power tower is growing rapidly, but this was not enough for mathematicians of the early twentieth century, and they invented the function of Ackermann. It is defined as:
This feature is growing very fast. With It is a power tower. With
It is a power tower. With  it is also a power tower, only now the number of twos in the tower is also a power tower, etc.
it is also a power tower, only now the number of twos in the tower is also a power tower, etc.
If you want to take revenge on the enemy, ask him to calculate this function using only arithmetic operations, if-s and for-s (while-s and recursion cannot). Akkerman proved that he will fail.
Akkerman’s inverse function defined as the minimum
defined as the minimum  such that
such that  . It is easy to understand that it is growing very slowly.
. It is easy to understand that it is growing very slowly.
First, note that each
Observation 1 . Rank tree contains at least
contains at least  knots.
knots.
This statement is proved by induction. For a tree of rank 0, obviously. To get a tree rank , you need to combine two trees of rank
, you need to combine two trees of rank 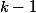 in each of which at least
in each of which at least 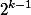 knots. So in the rank tree
knots. So in the rank tree  will be at least
will be at least  knots.
knots.
As a result, at any given time, rank nodes will be no more
will be no more  and maximum node rank
and maximum node rank  .
.
Remark 2 . The rank of the parent is always greater than the rank of the child.
It follows from the construction. Since on the way from the top to the root the rank always increases, its length does not exceed and any
and any  .
.
Prove that SNM operations over
SNM operations over  items can be held for
items can be held for  .
.
The .
.  plus the time for two
plus the time for two 
 .
.
The execution time of the
Divide all ranks on sets:
sets:  . AT
. AT  -th set will contain all ranks from the power tower
-th set will contain all ranks from the power tower  heights
heights  to tower height
to tower height  . The number of the set in which the rank of a node lies is called the level of the node.
. The number of the set in which the rank of a node lies is called the level of the node.
We say that a node is good if it is the root of the tree, the immediate child of the root, or he and his parent have different levels. The remaining nodes are called bad.
Total levels no more . Hence, the path from any node to the root contains at most
. Hence, the path from any node to the root contains at most 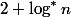 good knots. The total
good knots. The total  good knots.
good knots.
Estimate the number of passes on bad nodes. Let the bad knot has rank
has rank  and
and  belongs to many
belongs to many  . Note that a bad node is not a root, and therefore its rank is fixed. If
. Note that a bad node is not a root, and therefore its rank is fixed. If  then
then  changes its parent to a new one with a big rank. No more than
changes its parent to a new one with a big rank. No more than  passes through
passes through  like a bad knot
like a bad knot  will be good.
will be good.
Total nodes rank no more
no more 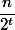 . So nodes with ranks from the set
. So nodes with ranks from the set  will be no more
will be no more 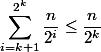 . Each node has no more than
. Each node has no more than  passages, like a bad knot. So in the amount of passes will be no more
passages, like a bad knot. So in the amount of passes will be no more  . Total levels
. Total levels 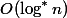 . This means that there will be no more passes on bad nodes.
. This means that there will be no more passes on bad nodes.  .
.
Total, got the top score for all transactions in the amount.
for all transactions in the amount.
Today we talk about depreciation analysis. First, I will tell you what it is and give a toy example. And then I will tell you how to use it for analyzing a system of disjoint sets.
Depreciation analysis
Depreciation analysis is used for algorithms that run several times. The algorithm time can vary greatly, but we estimate the average or total time for all runs. Most often, the algorithm implements some operation on the data structure.
')
The word "depreciation" came from finance. It means small periodic payments to repay the loan. In the lower case, it means that fast operations compensate for their costs for slow operations.
Consider the sequence of operations
 . Every operation
. Every operation  in fact performed in time
in fact performed in time 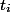 . This time is called actual. For each operation
. This time is called actual. For each operation  we calculate the amortization time
we calculate the amortization time 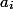 . We enter this time to make it easier to evaluate.
. We enter this time to make it easier to evaluate. 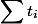 . From here two restrictions follow: a) formal - for any moment
. From here two restrictions follow: a) formal - for any moment 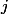 inequality holds
inequality holds 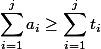 , and b) informal - the sum of depreciation values should be easily considered.
, and b) informal - the sum of depreciation values should be easily considered.To have a concrete example in front of us, consider the data structure, inside which the stack lies. The data structure supports the
op(m, x) operation, which throws the last def op(stack, m, x): for i in range(m): stack.pop() stack.push(x) We will assume that the arguments are always correct, and they will never ask us to throw out more than what is on the stack. In addition, we assume that
op(m, x) is executed in 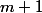 step without
step without  -notations All our estimates can always be multiplied by a constant to get correct.
-notations All our estimates can always be multiplied by a constant to get correct.Note that the time operation
op(m, x) can last from one to  steps. A rough estimate will give time
steps. A rough estimate will give time 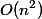 to fulfill all
to fulfill all Depreciation analysis offers three valuation methods.
Banker method. Time is money
Let every unit of time is a coin. We will issue each operation
 coins and allow to spend
coins and allow to spend 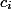 . All your coins transactions can be decomposed by data structure. The depreciation value of one operation will be
. All your coins transactions can be decomposed by data structure. The depreciation value of one operation will be 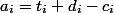 .
.To maintain the invariant
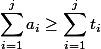 , we will set a restriction: you cannot spend more coins than there are at the moment:
, we will set a restriction: you cannot spend more coins than there are at the moment: 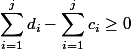 . Insofar as
. Insofar as  then
then 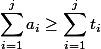 .
.For our example, we will issue one coin to each operation (
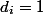 ). Put it on the element that we just added to the stack. So we paid for the future POP of this item.
). Put it on the element that we just added to the stack. So we paid for the future POP of this item.Note that at any time point on each element of the stack lies on the coin, i.e. All POPs are prepaid.
To throw out
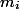 items we spend all the coins that lie on them (
items we spend all the coins that lie on them ( 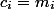 ). Then the depreciation value of each operation
). Then the depreciation value of each operation 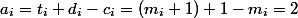 . It remains to be noted that
. It remains to be noted that  . We got the top linear score for execution
. We got the top linear score for execution Physics method. Use your potential
Any data structure can take several possible states. Let be
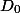 Is its initial state before all operations, and
Is its initial state before all operations, and 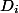 - state after
- state after 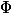 which takes as input the current state of the data structure and returns some non-negative number. Potential
which takes as input the current state of the data structure and returns some non-negative number. Potential 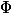 The initial state must be zero. For simplicity, we denote
The initial state must be zero. For simplicity, we denote 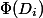 through
through 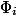 , but
, but 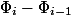 through
through 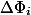 . Depreciation value
. Depreciation value 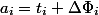 .
.Invariant
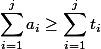 follows from the definition of potential. Really,
follows from the definition of potential. Really, 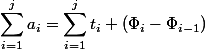 ; everything
; everything 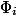 , except the first and last, are reduced and
, except the first and last, are reduced and  . Insofar as
. Insofar as 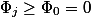 then
then 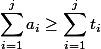 .
.The general idea is to find such a potential function, which would have fallen heavily on expensive operations, compensating for the actual time, but on cheap ones it would grow a little. For our example, the number of items in the stack is appropriate. After
POP and one PUSH  . Then the depreciation value
. Then the depreciation value 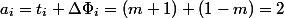 , and again we obtain a linear estimate.
, and again we obtain a linear estimate.Aggregation method. It is necessary to take and share everything
This method is a generalization of the previous two, and is to somehow count
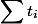 and divide by the number of requests.
and divide by the number of requests.In our case, this reasoning works. Each
op(m, x) operation performs one PUSH and several POPs. You cannot throw more elements from the stack than you put there. Just put in the stack  . Amortization value of a single operation
. Amortization value of a single operation The system of disjoint sets
We were given
make_set(key)- creates a set of one element,union(A, B)- combines the setsAandB,find(x)- returns the set in which the element lies.
The data structure that supports these operations is called the disjoint-set (SNM) system (English disjoint-set data structure, union-find data structure or merge-find set).
On Habré already wrote about SNM. A detailed description of the algorithm and its application can be found here . In this post, I briefly recall the algorithm itself and concentrate on the analysis.
Algorithm
Each set we will store as a tree. The tree node stores a reference to the parent. If the node is a root, the link points to
None . In addition, each node will have an additional rank field. We will discuss it below. class Node: def __init__(self, key): self.parent = None self.rank = 0 self.key = key To handle sets, we will select a representative for each set. In our case, this will be the root of the tree. If for two elements the representative matches, then they lie in one set. To combine two sets, you need to hang one tree to the root of another. We get a simple algorithm:
def find(x): if x.parent == None: return x return find(x.parent) def union(x, y): x = find(x) y = find(y) y.parent = x return x To speed up the algorithm, two heuristics are used.
Ranks . Each node is assigned a rank, initially equal to zero. The rank of the tree is the rank of its root. When combining sets, we will hang a tree of lower rank to a larger tree. If the ranks match, then first increase the rank of one of the trees by one.
def union(x, y): x = find(x) y = find(y) if x.rank < y.rank: x, y = y, x if x.rank == y.rank: x.rank += 1 y.parent = x return x Only one rank heuristic is enough to speed up the work of the SNM to
Compression paths . Let we run
find from the element 
def find(x): if x.parent == None: return x x.parent = find(x.parent) return x.parent Surprisingly, together these two heuristics reduce the depreciation time of a single operation to almost a constant.
Analysis
In 1973, Hopcroft and Ullman showed that SNM with two heuristics processes
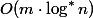 where
where 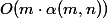 where
where My plan is to first analyze what kind of cunning functions are, then to prove a simple logarithmic estimate in the worst case, and at the end to analyze the estimate of Hopkroft and Ulman. Tarjan's assessment is also actively using depreciation analysis, but contains more technical details.
Tricky features
Iterative logarithm is the function inverse to a power tower. Let's imagine the number of the form
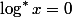 for anyone
for anyone 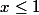 ;
;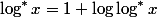 for
for 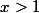 .
.
Exercise the reader to show that the iterative logarithm of the number of particles in the known part of the universe does not exceed five.
One might think that the power tower is growing rapidly, but this was not enough for mathematicians of the early twentieth century, and they invented the function of Ackermann. It is defined as:
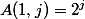 for
for  ;
;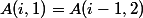 for
for  ;
;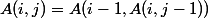 for
for  .
.
This feature is growing very fast. With
 It is a power tower. With
It is a power tower. With  it is also a power tower, only now the number of twos in the tower is also a power tower, etc.
it is also a power tower, only now the number of twos in the tower is also a power tower, etc.If you want to take revenge on the enemy, ask him to calculate this function using only arithmetic operations, if-s and for-s (while-s and recursion cannot). Akkerman proved that he will fail.
Akkerman’s inverse function
 . It is easy to understand that it is growing very slowly.
. It is easy to understand that it is growing very slowly.Worst case score
First, note that each
union is done in two find operations and some additional time constant. So, it is enough to evaluate only find . Estimation in the worst case follows from two simple observations.Observation 1 . Rank tree
This statement is proved by induction. For a tree of rank 0, obviously. To get a tree rank
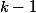 in each of which at least
in each of which at least 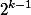 knots. So in the rank tree
knots. So in the rank tree As a result, at any given time, rank nodes
 and maximum node rank
and maximum node rank Remark 2 . The rank of the parent is always greater than the rank of the child.
It follows from the construction. Since on the way from the top to the root the rank always increases, its length does not exceed
find works for Evaluation of Hopcroft and Ulman
Prove that
The
make_set operation make_set performed in union operation find operations. So, it suffices to show that find operations will be performed in The execution time of the
find operation is proportional to the length of the path that is required to pass from the specified node to the root. Therefore, it is necessary to estimate the total number of passes through the nodes.Divide all ranks on
 . AT
. AT  to tower height
to tower height We say that a node is good if it is the root of the tree, the immediate child of the root, or he and his parent have different levels. The remaining nodes are called bad.
Total levels no more
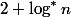 good knots. The total
good knots. The total find will take no more than Estimate the number of passes on bad nodes. Let the bad knot
find goes through the node Total nodes rank
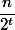 . So nodes with ranks from the set
. So nodes with ranks from the set 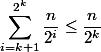 . Each node has no more than
. Each node has no more than 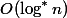 . This means that there will be no more passes on bad nodes.
. This means that there will be no more passes on bad nodes. Total, got the top score
Literature
- Kormen, Leyzerson, Rivest "Algorithms: construction and analysis"
- Tarjan "Data Structures and Network Algorithms"
- Rebecca Fiebrink Amortized Analysis Explained
Source: https://habr.com/ru/post/208624/
All Articles