The use of machine learning in building AI for the game of Japanese chess (shogi)

Good day.
For quite some time now, my friend Gorkoff and I have been fond of playing shogi . And we are so keen that we decided to write our own bot for this wonderful game. This article is a further description of the development process of the bot, which, with some interruptions, we have been doing for several months.
')
About alpha-beta clipping or why it is important to sort the moves
To decide which move to take in antagonistic games such as chess (as well as traditional and Japanese), checkers and tic-tac-toe, a minimax-optimization strategy called alpha-beta cut-off is used.
This algorithm was repeatedly considered on Habré, as in the article of my friend, and in other articles .
Briefly recall its essence with the following picture:
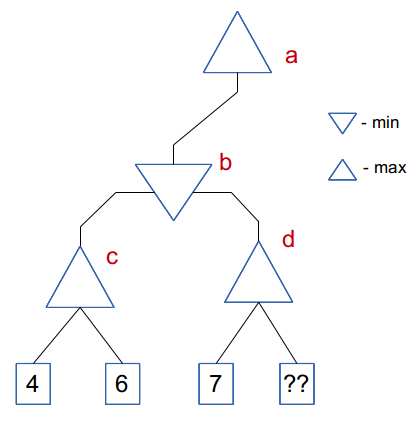
The numbers in the squares indicate the assessment of the position after making the appropriate sequence of moves.
In this example, a node is cut off , the value of which is marked with question marks.
You can verify the validity of this cut-off by making an expression that calculates the value at node b:
b = min (c, d) = min (max (4,6), max (7, X))
Obviously, the value of this expression does not depend on X , since the expression max (7, X) is obviously greater than or equal to 7, therefore, it is greater than max (4,6) and the value of b will be equal to b = 6 .
Thus, the alpha-beta cut-off algorithm makes it possible not to consider branches that are obviously worse than the one that has already been obtained.
Consequently, the consideration of more promising moves in the first gives the acceleration of the algorithm. Determining which course is more promising is the goal of this article.
Hypothesis
In a game, it is often obvious to a person that it is simply not necessary to consider some moves. For example, to move a pawn standing on the edge of the board at the moment when the opponent put the rook under attack.
For the computer, the concept of "obvious" does not exist, he will check all possible moves in turn and only after that he will conclude that eating the boat is the right decision.
If in any way to streamline the examination of moves so that the take move of the rook turns out to be first in consideration, the alpha-beta cut-off algorithm will end quickly, discarding all the branches whose evaluation is obviously worse than taking the rook.
In this example, a special case of the heuristic choice of the order of consideration of moves is considered, and it can hardly be used separately in the program. Manual description of a set of special cases is very laborious, moreover, there is always a chance that in any subset of the options, leaving the rook under attack, the pawn move is the only correct one.
Here an idea about the possibility of automatically obtaining information about promising moves from already played games appears. The use of machine learning methods is justified in this case by the hypothesis that moves with similar parameters (about them below) give a similar result.
Learning set
The first question that needs to be solved when using machine learning is to obtain a training set, which will determine the quality of the moves.
Oddly enough, this turned out to be the smallest problem, despite the inferior popularity of shogi compared to regular chess.
There is a playok.com site on the Net , which provides an opportunity to play various board games with other players for free. Among the games provided are shogi. Moreover, all the games played on this site are saved in the kifu format and are in the public domain, which makes it possible to write a simple script that downloads the required number of games.
The number of games stored on this site is very large (millions), so it was decided to create a database for local storage of the parameters of the games and moves.
It is worth saying that the task of storing such data is not very trivial, since the process of working with the base requires a large number of operations to obtain moves by the batch number.
Those. in the case of SQL, a sample of several dozen rows from a table containing millions of rows.
I considered the possibility of using NoSQL databases, such as MongoDB. In the case of NoSQL, such an operation would boil down to a simple pointer transition. Despite this advantage of NoSQL, PostgreSQL is used in the current implementation, and the move table has an index by lot number.
The scripts that implement the loading of batches from the playok.com website and their entry into the database, as well as the scripts that perform data preparation (ie, those functions whose execution time is not critical), are written in Ruby, because This language provides high speed of writing code, and also has all the necessary components for working with the database. Links to source codes are provided at the end of the article.
About the description of the moves
In order for the application of machine learning methods to be possible, it is necessary to describe each move using a set of features. Such a description, oddly enough, is called an attribute description of the object.
An attribute description is a vector of values, which, in turn, is the coordinates of a point in the attribute space.
For example, an indicative description of a box may be its dimensions and weight. Thus, a box measuring 2 by 3 by 1 meter and weighing 10 kilograms will have a characteristic description (2,3,1,10) in the four-dimensional feature space.
Due to the fact that the move with the same designation (e2e4) in different batches can lead to opposite results, it is necessary to include signs containing information about the position of other pieces on the board in the indicative description of the move.
For signs, it is also necessary to observe the invariance with respect to the color of the figure that made the move, since in the training sample both black and white moves can be good. For example, the horizontal number of a move is better to be replaced by the number of horizontal lines to the initial position (in this case, it is considered that black starts from horizontal 9, and white starts from horizontal 1).
The version of the feature description used consists of the following parameters:
Long list
- The weight of the move
- Weight of eaten figure (0, if not)
- The amount of horizontal from the initial position to the position from which the move is made
- Vertical number from which the move is made
- The amount of horizontal from the initial position to the position to which the move is made
- Vertical number to move to
- Whether the figure was flipped (1/0)
- The total weight of the attacked figures
- The weight of the strongest attacked figure
- The arithmetic average of the weights of the attacked figures
- The weight of the weakest attacked figure
- The total weight of the enemy pieces attacking the position from which the move is made
- The weight of the strongest of the enemy pieces attacking the position from which the move is made
- The average weight of enemy pieces attacking the position from which the move is made
- The weight of the weakest of the enemy pieces attacking the position from which the move is made
- The total weight of the enemy pieces attacking the new position
- The weight of the strongest of the enemy pieces attacking the new position
- The average weight of enemy pieces attacking a new position
- The weight of the weakest enemy figure attacking the new position
- Number of pieces attacking a new piece
- The total weight of their figures, protecting the original position
- The weight of the strongest of his figures, protecting the original position
- The average weight of their figures, protecting the original position
- The weight of the weakest of his figures, protecting the original position
- The total weight of their figures, protecting the new position
- The weight of the strongest of their figures defending a new position
- The average weight of their figures, protecting the original new
- The weight of the weakest of their figures defending the new position
- The number of their figures defending the new position
- The distance to the opponent's king horizontally in a new position
- The distance to the king of the enemy vertically
- Horizontal distance to his king
- Vertical distance to his king
- Move number in the game
About the choice of classification algorithm
Problem statement implies the classification of moves for promising and unpromising (good and bad), however, some additional conditions are also imposed on the algorithm:
- It must be possible to rank moves from best to worst.
- High speed must be ensured, since the classification (and sorting) must be done at each stage of the tree viewing.
Among the classification algorithms for our task, the nearest neighbor method is well suited.
The method consists in determining which object of which class in the feature space is located closest to the classified object.
This method is good because it naturally determines which of the two considered moves is better. To do this, it is enough to compare the distances to their nearest neighbors.
However, the method has a significant drawback: you need to check a large number of objects before you can claim that the closest one is found.
One way to solve this problem is to use clustering.
Replacing the set of source points with the set of points that are cluster centers, we will significantly reduce the number of operations required to classify an object. Such a replacement will obviously degrade the quality of the classification, and the smaller the clusters in the output set, the worse the quality will be. Thus, the number of clusters is a value reflecting a compromise between accuracy and speed.
About the choice of moves
Before proceeding to the processing of batches it is necessary to decide which moves are considered good and which are bad in our database. Several options immediately come to mind:
- The moves that led to the material advantage.
- The moves that led to the mat.
- The moves made by top rated players.
If you think a little more, it becomes clear that the first and second options are not guaranteed to be good.
Since, firstly, there are situations in which a player, in which the sacrifice of a strong figure subsequently results in the loss of the player who accepted the sacrifice.
Secondly, the mate can be placed because of the negligence of the loser player, which happens quite often.
If a player with a high rating wins the game, then we can say that he did not make unequivocally stupid moves (at a sufficient level, yawning is guaranteed to fail), and our task, I remind you, is not to establish absolutely accurate moves in specific situations, And a sort of moves by quality on average.
Based on the above arguments, we find that in order to solve our problem, we will have to trust the authorities.
In the current implementation, the moves are selected as follows:
- Sets the lower and upper thresholds of ratings.
- In each game, the winner's rating in which is higher than the upper threshold, the last 2/3 of the winner's moves are selected and marked as good.
- In each game, the losing rating in which is less than the lower threshold, the last 2/3 of the loser’s moves are selected and are marked as bad.
Weeding out the first moves is justified by the fact that there are other, more efficient algorithms for the debut of the game, which are beyond the scope of the article.
About clustering
In contrast to the classification that must be performed at each step of viewing the game tree, clustering, in our case, has less stringent requirements.
First of all, clustering should be performed only 1 time, which gives the right to use algorithms that require more time than what we have at the time of the game.
By itself, the clustering problem is not clearly formulated, which gives many options for its interpretation. We will use the following definition:
Clustering consists of dividing a set of objects into non-intersecting sets (clusters) in such a way as to minimize the distance between objects within the cluster and maximize the distance between clusters.
Formally, this definition can be written as follows:
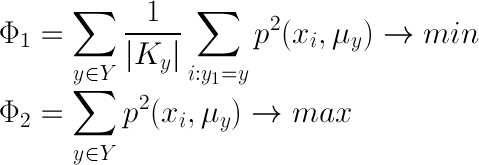
Where K y - cluster number y
p (x, y) is a function that determines the distance in a given metric
μ y - the center of the cluster with the number y
x i - object number i
In my implementation, I used the k-means clustering algorithm, its detailed description can be found, for example, in Wikipedia .
The peculiarity of the algorithm is that it uses random values as the initial partition into clusters, the choice of which strongly influences the result of further splitting, which makes it possible to repeatedly perform clustering to achieve better results, and we are not limited in execution time at this stage.
For example, clustering random points in a two-dimensional space looks like this:
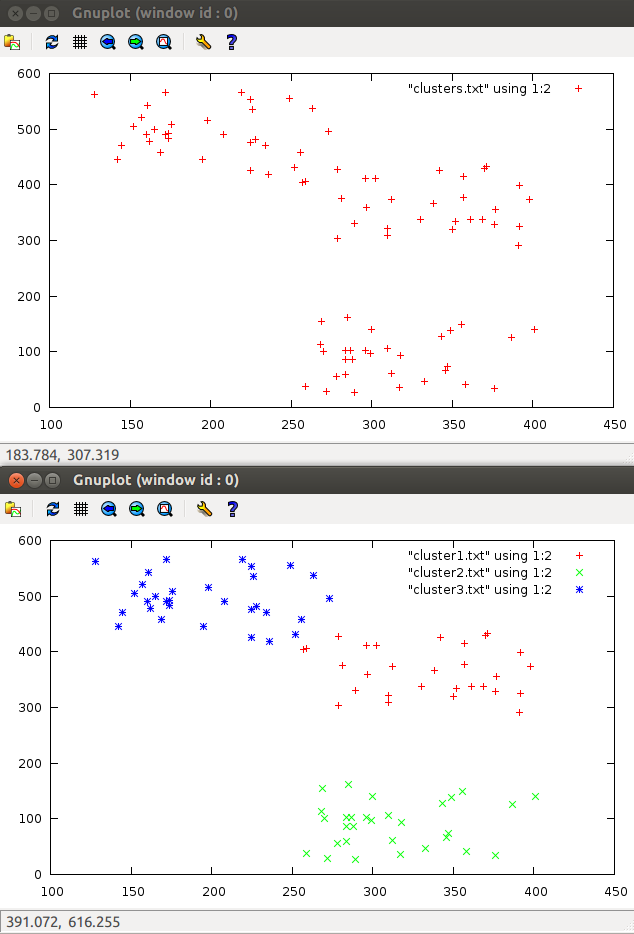
Implementation in ruby
def midle(cluster) # "" res = [0]*cluster[0].size(); cluster.each do |e| i = 0; e.each do |x| res[i] += x; i+=1; end end res.map! {|x| x/cluster.size.to_f} return res; end def dist(x1,x2) if(x1.size != x2.size) raise "WrongSizeException"; end mode = 1 if mode ==1 then # dist = 0; for i in 0..x1.size-1 dist += (x1[i]-x2[i])**2 end return dist; end if mode == 2 then # dist = 0; x1_s = 0; x2_s = 0; for i in 0..x1.size-1 dist += x1[i]*x2[i] x1_s += x1[i]**2; x2_s += x2[i]**2; end dist =1 - dist / Math.sqrt(x1_s) / Math.sqrt(x2_s) end end def quality1 (clusters) # ( , - ) sum = 0; clusters.each do |cluster| center = midle(cluster) local_sum = 0 cluster.each do |vector| local_sum += dist(vector, center); end sum += local_sum / cluster.size.to_f; end return sum; end def quality2 (clusters) # centers = []; clusters.each do |cl| centers += [midle(cl)]; end sum = 0 centers.each do |c1| centers.each do |c2| sum += dist(c1,c2) end end return sum; end def quality (clusters) # return quality1(clusters)/quality2(clusters); end def find_nearest(vectors, point) min = Float::INFINITY imin = 0 i = 0 vectors.each do |vector| d = dist(vector, point) if(d < min) then min = d; imin = i; end i += 1; end return imin end def k_means(vectors, k) len = vectors.size; clusters = []; centers_index = []; if len < k then raise "count of clusters more than objects"; end while centers_index.size != k do # k centers_index = (1..k).map { Random.rand(len)}; # k centers_index.uniq! end centers = centers_index.map{ |e| vectors[e] } clusters_new = [] begin # clusters = clusters_new; clusters_new = k.times.map {[]}; vectors.each do |vector| clusters_new[find_nearest(centers, vector)] += [vector]; end # centers = []; clusters_new.each do |cluster| return nil if cluster == nil; # , - return nil if cluster.size == 0; centers += [midle(cluster)] end end until clusters_new == clusters return clusters_new end As a result of clustering, we obtain N (I chose N = 20 ) points, which are the centers of clusters of good and bad moves in the feature space.
The distance to these points will be used when sorting the order of viewing moves.
About classification
Now that we have a significantly smaller number of points compared to the original base, we can apply sorting based on proximity to these points.
As in the previous stages, we face a choice. Namely, the choice of the metric in which the distance to the clusters will be calculated.
It is possible to use both the usual Euclidean metric and the Mahalanobis metric, which takes into account the correlation between the coordinates of points.
Pictures for clarity: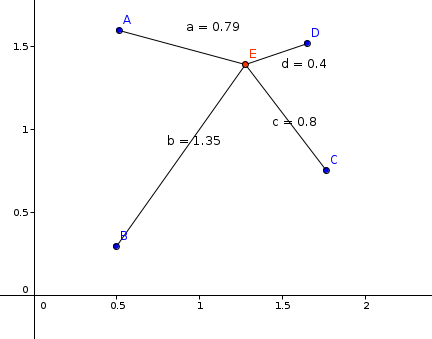
Euclidean metric in two-dimensional space.
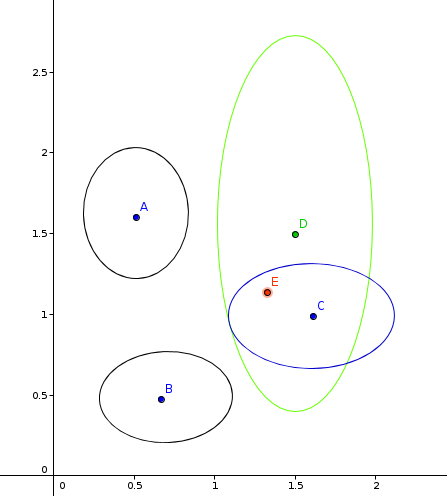
Mahalanobis metric in two-dimensional space. Ellipses show the variance of the values.

Euclidean metric in two-dimensional space.

Mahalanobis metric in two-dimensional space. Ellipses show the variance of the values.
Which metric is better and by what parameters is a separate and very difficult question, so for the beginning we will stop on a simple variant - the Euclidean metric.
The value by which the moves will be sorted will choose the following: ((Distance to the nearest cluster of bad moves) - (Distance to the nearest cluster of good moves)) .
Thus, the larger the specified value of the turn, the earlier it should be considered when building the game tree.
Here it is also possible to use other expressions to obtain an estimate of the course, for example, the average distance to clusters of good moves, etc.
A piece of java implementation
public static double euclidian(ArrayList<Double> p1, ArrayList<Double> p2) { Double sum = 0.0; for (int i = 0; i < p1.size(); i++) { sum += (p1.get(i) - p2.get(i)) * (p1.get(i) - p2.get(i)); } return sum; } public static double getMinDist(ArrayList<Double> point, ArrayList<ArrayList<Double>> clusters) { Double min = Double.MAX_VALUE; for (ArrayList<Double> cluster : clusters) { min = Math.min(min, euclidian(cluster, point)); } return min; } private void sortMoves(CMovesList movesList) { // ( ) - ( ) for (CMove move : movesList.Moves) { ArrayList<Double> move_params = CDataMining.getFeature(localBoard, move).toArray(); // // Double good_dist = CAdviser.getMinDist(move_params, clusters_good); // Double bad_dist = CAdviser.getMinDist(move_params, clusters_bad); move.H = bad_dist - good_dist; } movesList.sortH(); } /** * - * * @param color * @param D * @param A * @param B * @return */ public int AB(boolean color, int D, int A, int B) { ABtimes++; if ((D == 0) || Math.abs(localBoard.Evaluate(color)) >= 15000) return localBoard.Evaluate(color); CMovesList ML; ML = localBoard.getAllMoves(color); if (D == MaxD) { // sortMoves(ML); // < ----- . } else { ML.sortH(); } while ((ML.getMovesCount() > 0) && (A < B)) { CMove Move = ML.getMoveByIndex(0); CFigure previousFigure = localBoard.makeMove(Move); int tmp = -AB(!color, D - 1, -B, -A); localBoard.unmakeMove(Move, previousFigure); if (tmp > A) { A = tmp; if (D == MaxD) BestMove.cp(Move); } ML.removeByIndex(0); } return A; } Result
The main criterion in assessing the effectiveness of the described method was the number of recursive calls to the Alpha-Beta cut-off procedure, since this criterion does not depend on the implementation and, therefore, is the most objective.
Experiments have shown that the effectiveness of the method strongly depends on the situation on the board. This is not surprising, since the training of the classifier took place on real batches, therefore, its efficiency for solving artificially designed tasks can be significantly lower than that of simple heuristics, sorting out moves by the weight of attacked figures.
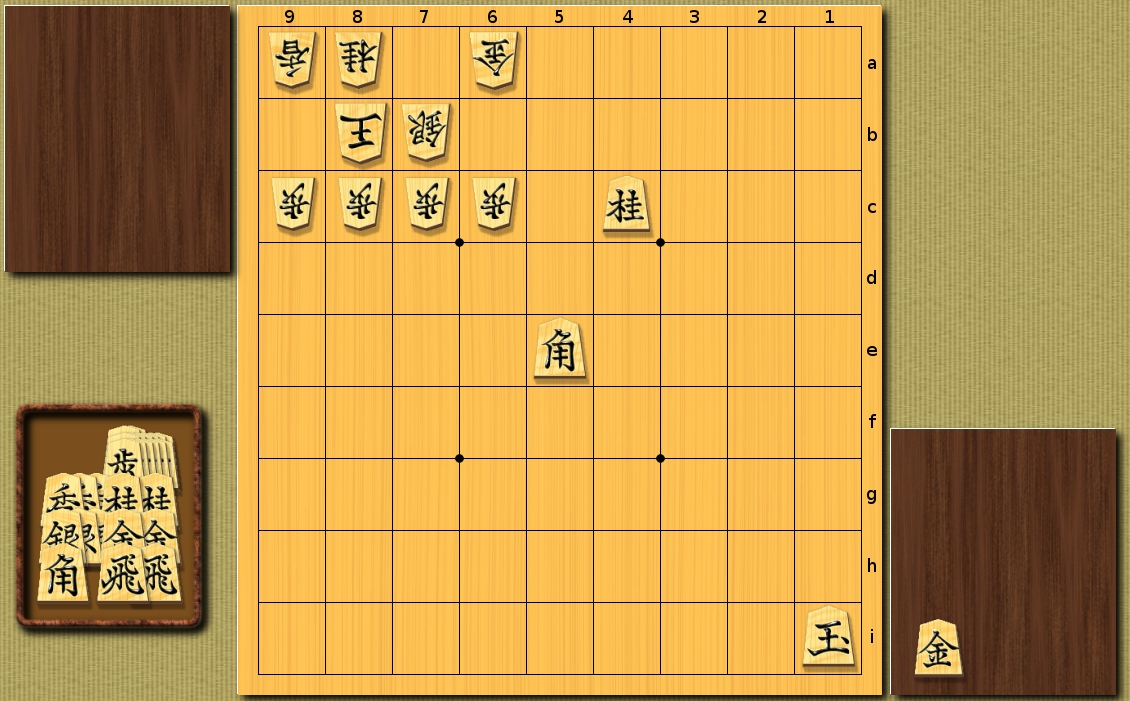
Work examples (for clarity, the result is shown using the BCDGames program):
Maximum rendering depth: 4 half shots.
Random position taken from a real batch.
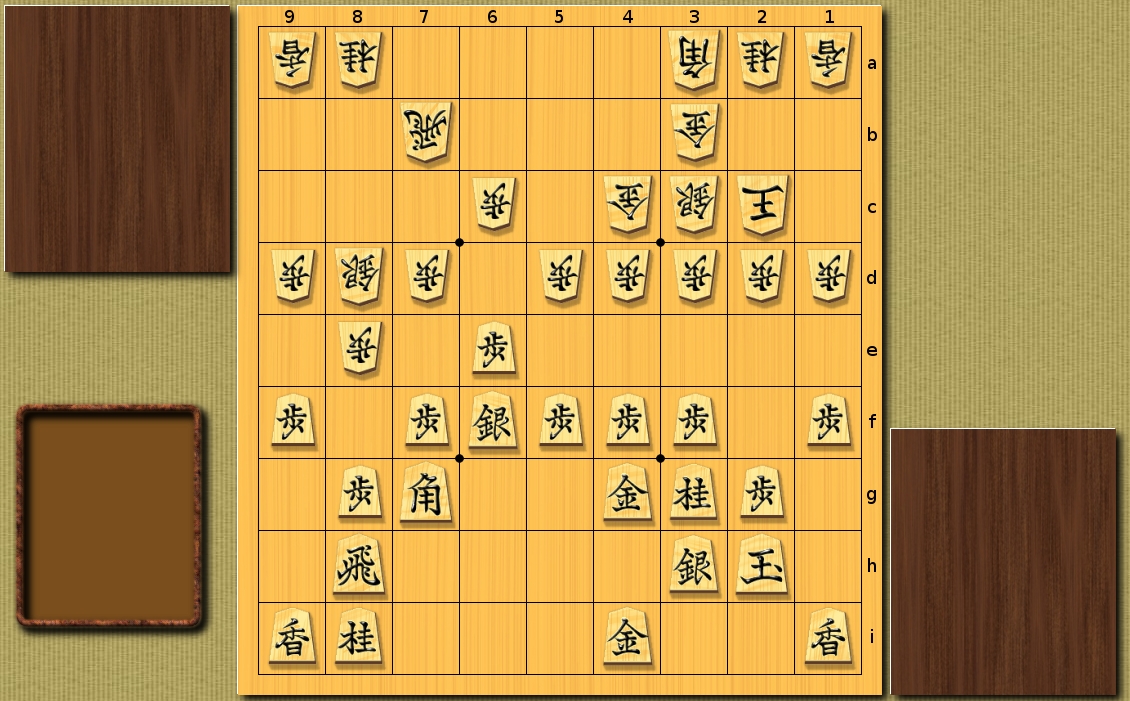
Simple heuristics:
The number of recursive calls - 22027
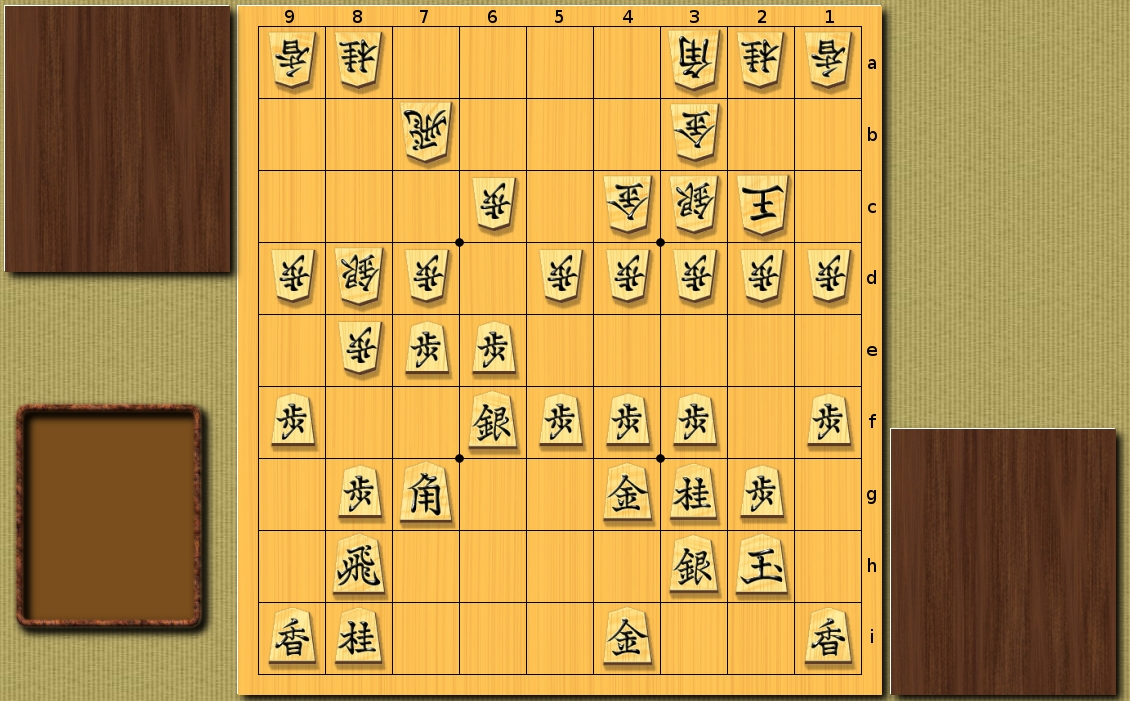
Heuristics using Machine Learning for the first, for subsequent moves - simple heuristics:
The number of recursive calls - 18719
The made moves are different, since in the constructed tree the games at the maximum depth have the same score.

Simple heuristics:
The number of recursive calls - 32561
Heuristics using Machine Learning for the first, for subsequent moves - simple heuristics:
The number of recursive calls - 28524

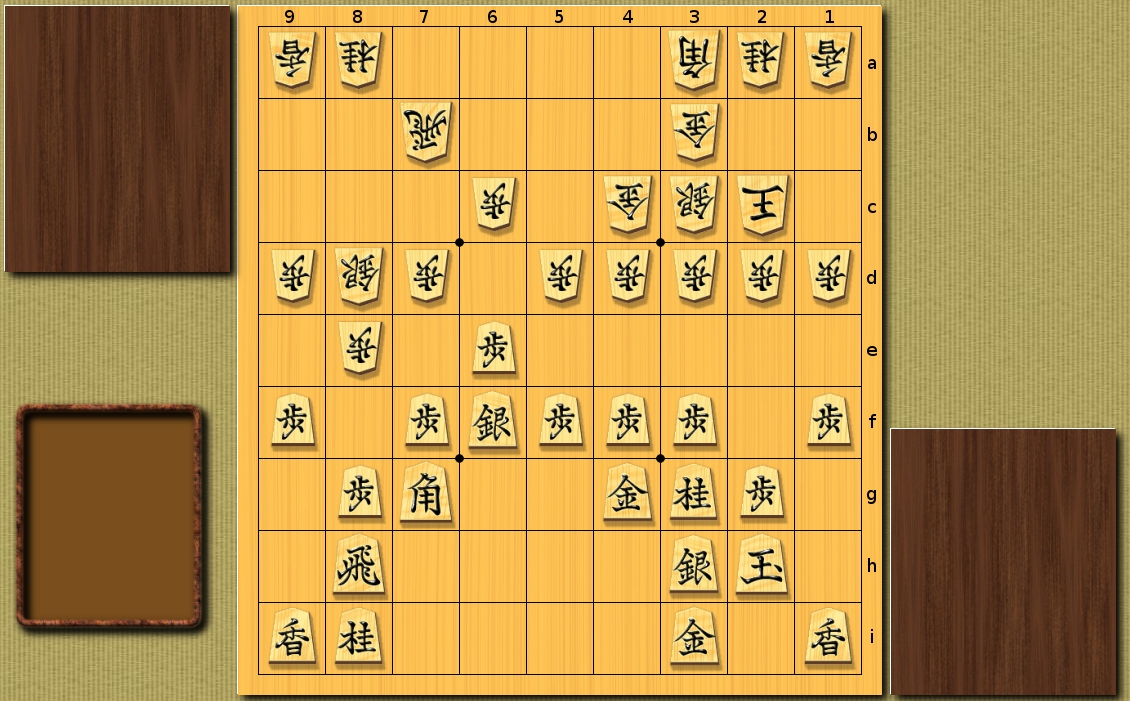
Artificial situation with a small number of pieces on the board and a few pieces in hand.
(Viewing rude - 3 semi-moves)
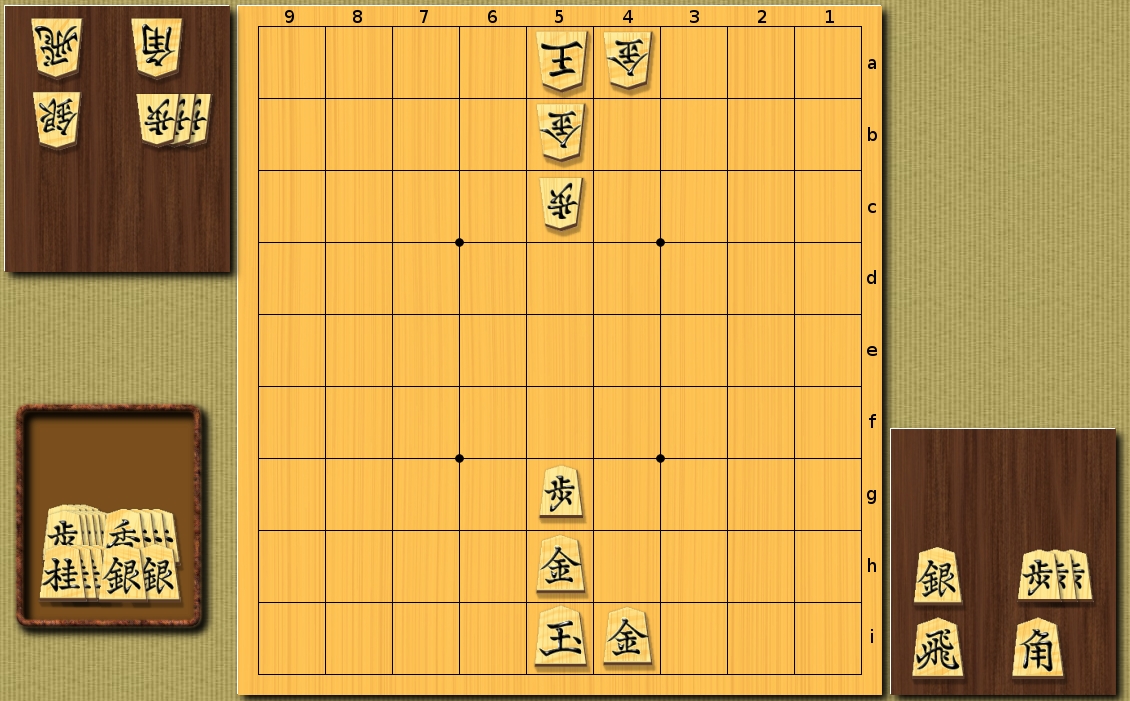
Simple heuristics:
The number of recursive calls - 379376
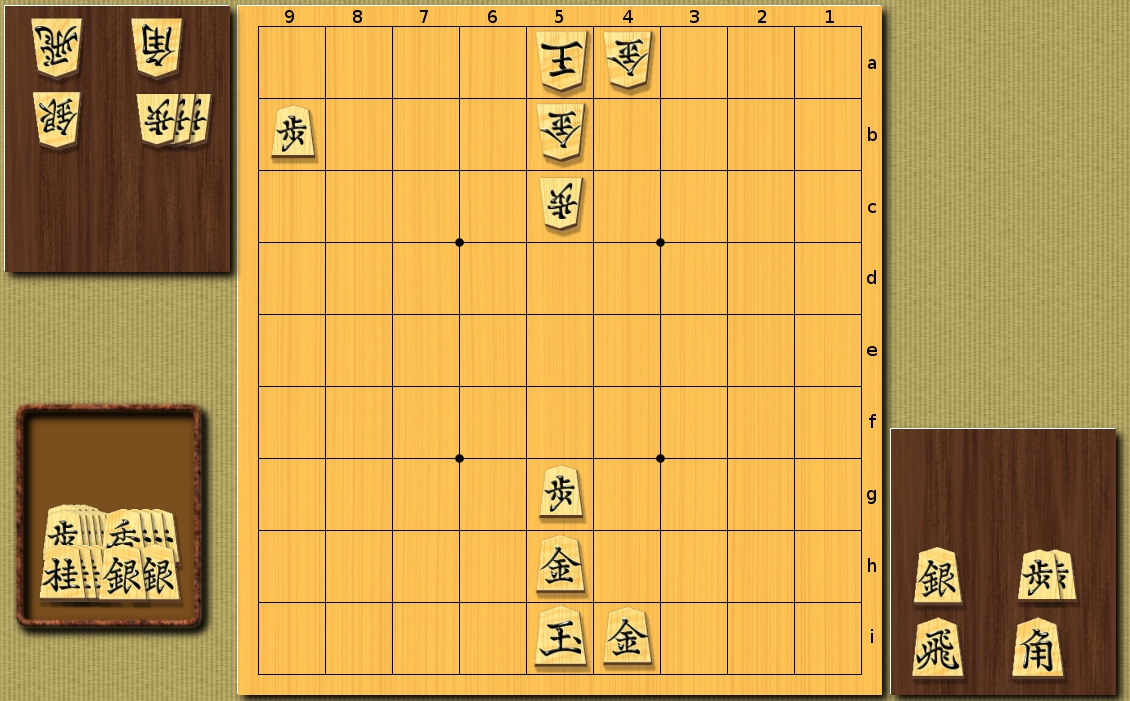
Heuristics using Machine Learning for the first, for subsequent moves - simple heuristics:
The number of recursive calls - 541866
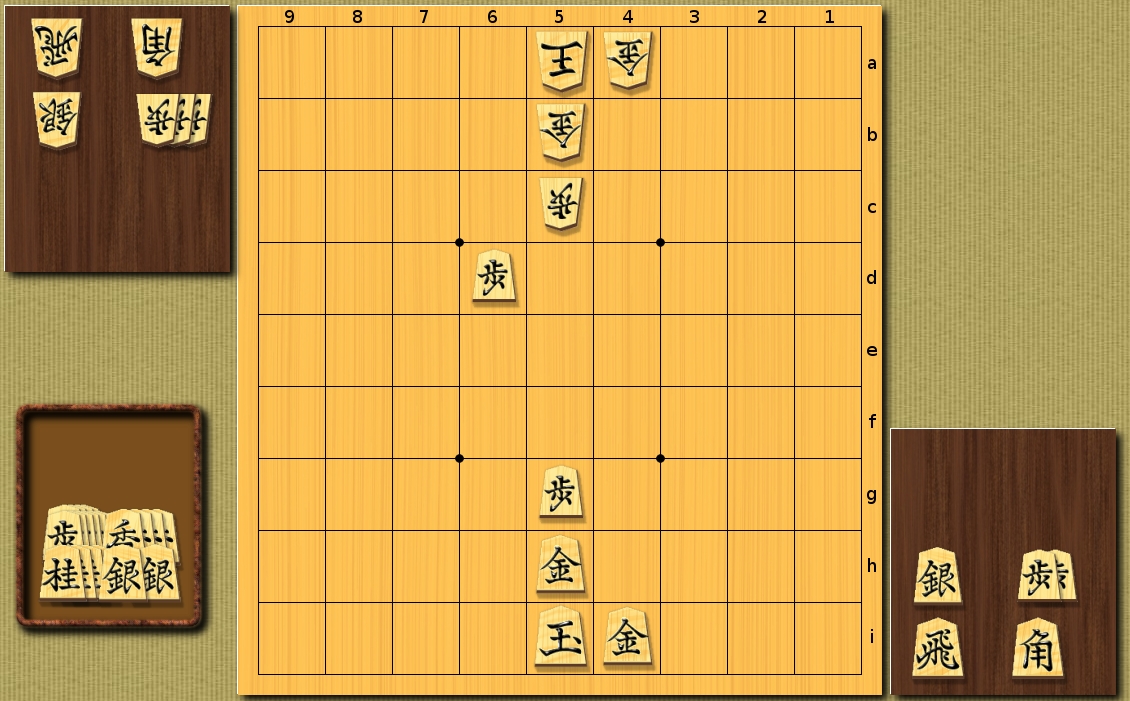
As can be seen, in the case of an artificially formed situation on the board, heuristics based on machine learning, as expected, gives a worse efficiency compared to simple heuristics.
Random position taken from a real batch.

Simple heuristics:
The number of recursive calls - 22027

Heuristics using Machine Learning for the first, for subsequent moves - simple heuristics:
The number of recursive calls - 18719

The made moves are different, since in the constructed tree the games at the maximum depth have the same score.

Simple heuristics:
The number of recursive calls - 32561

Heuristics using Machine Learning for the first, for subsequent moves - simple heuristics:
The number of recursive calls - 28524

Artificial situation with a small number of pieces on the board and a few pieces in hand.
(Viewing rude - 3 semi-moves)

Simple heuristics:
The number of recursive calls - 379376

Heuristics using Machine Learning for the first, for subsequent moves - simple heuristics:
The number of recursive calls - 541866

As can be seen, in the case of an artificially formed situation on the board, heuristics based on machine learning, as expected, gives a worse efficiency compared to simple heuristics.
Disadvantages of the method
- Long.
In the process of calculating the nearest points, operations with real numbers are used, which significantly increases the viewing time of the game tree.
- Limited use
As noted above, for some situations, the machine learning method can give a worse result than simple heuristics.
Possible ways to improve
Get rid of the real operations can, for example, using the Manhattan distance.
The number of real operations can also be reduced by reducing the number of clusters. Such a reduction will lead to a loss of accuracy and, consequently, to a deterioration of the work of the Alpha-Beta cut-off algorithm, which will increase the running time. Therefore, ideally, it is necessary to solve the optimization problem for this parameter.
To solve the applicability problem of machine learning heuristics, the following improvements are possible:
- Consideration of moves in the context of the situation on the board, which includes the construction of a graph of interaction of the figures and the addition of information from this graph to the parameters of the course.
- Creating different clusters for different types of positions on the board (Depending on the number of pieces, in the case of an attacking strategy, in the case of a defensive strategy, etc.) and applying a particular set of clusters depending on the game situation.
References and literature
- In machine learning there is a remarkable course of lectures by K. V. Vorontsov, from which I took information about the methods used. His lectures were recently posted on Habr.
- The repository with the bot itself, written in java: https://github.com/gorkoff/Shogi/tree/DataMining
- Repository with Ruby helper scripts: https://github.com/generall/ScriptsForShogi
Thanks for attention.
Source: https://habr.com/ru/post/208580/
All Articles