Fuzzy Cluster fuzzy clustering algorithm for PHP
Good day.
The post and code below is intended not so much to use the algorithm for working purposes, but rather to understand how the fuzzy c-means algorithm works and possibly give impetus to the implementation of this algorithm in other languages or to improve the above code and its further use for business purposes.

')
To begin with, it is worth telling very quickly what clustering is and what is special about fuzzy clustering.
Clustering, as the word Wiktionary describes,
This definition is quite understandable and I think it does not need an additional explanation.
What then is “fuzzy clustering” ?
Fuzzy clustering differs from just clustering by the fact that objects that undergo clustering belong to a specific cluster with a certain belonging, and not unambiguously, as is the case with ordinary clustering. For example, in fuzzy clustering, object A belongs to cluster K1 with membership of 0.9, cluster K2 with belonging to 0.04 and cluster K3 with belonging to 0.06. With the usual (clear) clustering, object A would be assigned to cluster K1.
You can find the mathematical description of this algorithm in this habrapost .
Let's go directly to the implementation of the algorithm. For this, I would consider the implementation on a more or less real example. Such an example might be the following - let's cluster the pixels by their RGB value, i.e. actually by color. As a result, we can see the result of the algorithm execution visually.
Below is the code of the algorithm, which I will discuss in more detail later.
Let's start the consideration of the algorithm with the function that actually runs the clustering algorithm itself -
The input parameters for it are an array of clustered objects (in our case, a randomly filled array containing object class objects about]) and an uncertainty coefficient. The return value is the membership matrix. Also, the parameter
The steps for finding new cluster centers and recalculating the membership matrix are limited by the MAX_EXECUTION_CYCLES and EPSILON constants, where MAX_EXECUTION_CYCLES limits the number of steps, EPSILON limits the accuracy of finding the membership matrix.
Each step of the algorithm is as follows:
1) we calculate the centers of the clusters using the function
2) then, for each object, we calculate the Euclidean distance to the center of each cluster (the
3) calculate the coefficient of
4) we normalize the coefficients
5) calculate the value of the decision function (function
6) then the current value of the decision function is compared with its previous value and if their difference is less than the set EPSILON, the algorithm stops working.
Now a little more about each step:
1) the centers are calculated according to the following formula
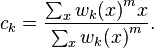
where wk (x) is the membership coefficient, m is the uncertainty coefficient, x is an object (in the algorithm itself, the components R, G, B are x)
2) We calculate the Euclidean distance for 3 dimensions, i.e. The formula is as follows:
where r, g, b - the components of RGB
3) the coefficient of belonging is calculated by the formula
where d is the distance from the object to the cluster center, m is the coefficient of uncertainty.
4) normalization of all coefficients of the object's membership - we transform the coefficients so that in total they give 1, i.e. we actually divide each coefficient by the sum of all coefficients of a given object
5) the decision function returns the sum of all Euclidean distances of each object to each center of the cluster multiplied by the membership factor
6) modulo subtract the previous and current value of the decision function, and if this difference is less than EPSILON, the algorithm stops and the found membership matrix is returned.
In the end, I would like to add a couple of screenshots showing the results of the algorithm.
The figures show that the algorithm worked correctly and we will take the points that are similar in color to the same clusters.
Thus, I presented to you the basic implementation of fuzzy c-means fuzzy clustering algorithm. I hope she will be useful to you.
Thanks for attention.
The post and code below is intended not so much to use the algorithm for working purposes, but rather to understand how the fuzzy c-means algorithm works and possibly give impetus to the implementation of this algorithm in other languages or to improve the above code and its further use for business purposes.

')
General information
To begin with, it is worth telling very quickly what clustering is and what is special about fuzzy clustering.
Clustering, as the word Wiktionary describes,
grouping, partitioning of a set of objects into disjoint subsets, clusters consisting of similar objects
This definition is quite understandable and I think it does not need an additional explanation.
What then is “fuzzy clustering” ?
Fuzzy clustering differs from just clustering by the fact that objects that undergo clustering belong to a specific cluster with a certain belonging, and not unambiguously, as is the case with ordinary clustering. For example, in fuzzy clustering, object A belongs to cluster K1 with membership of 0.9, cluster K2 with belonging to 0.04 and cluster K3 with belonging to 0.06. With the usual (clear) clustering, object A would be assigned to cluster K1.
You can find the mathematical description of this algorithm in this habrapost .
Implementing fuzzy c-means in PHP.
Let's go directly to the implementation of the algorithm. For this, I would consider the implementation on a more or less real example. Such an example might be the following - let's cluster the pixels by their RGB value, i.e. actually by color. As a result, we can see the result of the algorithm execution visually.
Below is the code of the algorithm, which I will discuss in more detail later.
Implementing fuzzy c-means algorithm for clustering points by their RGB value
define('EPLSION', 0.1); define('MAX_EXECUTION_CYCLES', 150); define('POINTS_COUNT', 100); define('CLUSTERS_NUM', 3); define('FUZZ', 1.5); class Point { public $r; public $g; public $b; } // Random values 0 - 1 function random_float ($min,$max) { return ($min+lcg_value()*(abs($max-$min))); } // Fuzzy C Means Algorithm function distributeOverMatrixU($arr, $m, &$centers) { $centers = generateRandomPoints(CLUSTERS_NUM); $MatrixU = fillUMatrix(count($arr), count($centers)); $previousDecisionValue = 0; $currentDecisionValue = 1; for($a = 0; $a < MAX_EXECUTION_CYCLES && (abs($previousDecisionValue - $currentDecisionValue) > EPLSION); $a++){ $previousDecisionValue = $currentDecisionValue; $centers = calculateCenters($MatrixU, $m, $arr); foreach($MatrixU as $key=>&$uRow){ foreach($uRow as $clusterIndex=>&$u){ $distance = evklidDistance3D($arr[$key], $centers[$clusterIndex]); $u = prepareU($distance, $m); } $uRow = normalizeUMatrixRow($uRow); } $currentDecisionValue = calculateDecisionFunction($arr, $centers, $MatrixU); } return $MatrixU; } function fillUMatrix($pointsCount, $clustersCount) { $MatrixU = array(); for($i=0; $i<$pointsCount; $i++){ $MatrixU[$i] = array(); for($j=0; $j<$clustersCount; $j++){ $MatrixU[$i][$j] = random_float(0, 1); } $MatrixU[$i] = normalizeUMatrixRow($MatrixU[$i]); } return $MatrixU; } function calculateCenters($MatrixU, $m, $points) { $MatrixCentroids = array(); for($clusterIndex=0; $clusterIndex < CLUSTERS_NUM; $clusterIndex++){ $tempAr = 0; $tempBr = 0; $tempAg = 0; $tempBg = 0; $tempAb = 0; $tempBb = 0; foreach($MatrixU as $key=>$uRow){ $tempAr += pow($uRow[$clusterIndex],$m); $tempBr += pow($uRow[$clusterIndex],$m) * $points[$key]->r; $tempAg += pow($uRow[$clusterIndex],$m); $tempBg += pow($uRow[$clusterIndex],$m) * $points[$key]->g; $tempAb += pow($uRow[$clusterIndex],$m); $tempBb += pow($uRow[$clusterIndex],$m) * $points[$key]->b; } $MatrixCentroids[$clusterIndex] = new Point(); $MatrixCentroids[$clusterIndex]->r = $tempBr / $tempAr; $MatrixCentroids[$clusterIndex]->g = $tempBg / $tempAg; $MatrixCentroids[$clusterIndex]->b = $tempBb / $tempAb; } return $MatrixCentroids; } function calculateDecisionFunction($MatrixPointX, $MatrixCentroids, $MatrixU) { $sum = 0; foreach($MatrixU as $index=>$uRow){ foreach($uRow as $clusterIndex=>$u){ $sum += $u * evklidDistance3D($MatrixCentroids[$clusterIndex], $MatrixPointX[$index]); } } return $sum; } function evklidDistance3D($pointA, $pointB) { $distance1 = pow(($pointA->r - $pointB->r),2); $distance2 = pow(($pointA->g - $pointB->g),2); $distance3 = pow(($pointA->b - $pointB->b),2); $distance = $distance1 + $distance2 + $distance3; return sqrt($distance); } function normalizeUMatrixRow($MatrixURow) { $sum = 0; foreach($MatrixURow as $u){ $sum += $u; } foreach($MatrixURow as &$u){ $u = $u/$sum; } return $MatrixURow; } function prepareU($distance, $m) { return pow(1/$distance , 2/($m-1)); } function generateRandomPoints($count){ $points = array_fill(0, $count, false); array_walk($points, function(&$value, $key){ $value = new Point(); $value->r = rand(20, 235); $value->g = rand(20, 235); $value->b = rand(20, 235); }); return $points; } $points = generateRandomPoints(POINTS_COUNT); $centers = array(); $matrixU = distributeOverMatrixU($points, FUZZ, $centers); Let's start the consideration of the algorithm with the function that actually runs the clustering algorithm itself -
distributeOverMatrixUThe input parameters for it are an array of clustered objects (in our case, a randomly filled array containing object class objects about]) and an uncertainty coefficient. The return value is the membership matrix. Also, the parameter
centers was added to the in / out function, in which, after the algorithm is executed, the centers of our clusters will be.The steps for finding new cluster centers and recalculating the membership matrix are limited by the MAX_EXECUTION_CYCLES and EPSILON constants, where MAX_EXECUTION_CYCLES limits the number of steps, EPSILON limits the accuracy of finding the membership matrix.
Each step of the algorithm is as follows:
1) we calculate the centers of the clusters using the function
calculateCenters2) then, for each object, we calculate the Euclidean distance to the center of each cluster (the
evklidDistance3D function is 3-dimensional space with us)3) calculate the coefficient of
u for this object (the prepareU function)4) we normalize the coefficients
u for a given object (the normalizeUMatrixRow function)5) calculate the value of the decision function (function
calculateDecisionFunction )6) then the current value of the decision function is compared with its previous value and if their difference is less than the set EPSILON, the algorithm stops working.
Now a little more about each step:
1) the centers are calculated according to the following formula
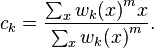
where wk (x) is the membership coefficient, m is the uncertainty coefficient, x is an object (in the algorithm itself, the components R, G, B are x)
2) We calculate the Euclidean distance for 3 dimensions, i.e. The formula is as follows:
r = sqrt((r2-r1)^2 + (g2-g1)^2 + (b2-b1)^2);where r, g, b - the components of RGB
3) the coefficient of belonging is calculated by the formula
u = (1/d)^(2/(m-1)) ,where d is the distance from the object to the cluster center, m is the coefficient of uncertainty.
4) normalization of all coefficients of the object's membership - we transform the coefficients so that in total they give 1, i.e. we actually divide each coefficient by the sum of all coefficients of a given object
5) the decision function returns the sum of all Euclidean distances of each object to each center of the cluster multiplied by the membership factor
6) modulo subtract the previous and current value of the decision function, and if this difference is less than EPSILON, the algorithm stops and the found membership matrix is returned.
In the end, I would like to add a couple of screenshots showing the results of the algorithm.
The figures show that the algorithm worked correctly and we will take the points that are similar in color to the same clusters.
Algorithm demonstration





Thus, I presented to you the basic implementation of fuzzy c-means fuzzy clustering algorithm. I hope she will be useful to you.
Thanks for attention.
Source: https://habr.com/ru/post/208496/
All Articles