Calculation of the fractal dimension of Minkowski for a flat image

Good day reader. Today's post will be devoted to the calculation of the approximate value of the fractal dimension of a flat image, which is closely related to the dimension of Minkowski . This is interesting for at least two reasons. First, it turns out that the dimension of a bounded set in a metric space can be not only an integer, but also any non-negative one. Secondly, the value of the dimension of the contour of the image (and this is a limited set in the metric space) is a good sign . In today's post, there is no study on the robustness of this feature, but let's consider an illustrative example. Many different characteristics of cells of breast tumors , resulting from the analysis of images of fine needle puncture biopsy. A lot of data consists of 30 signs (fields of the table) marked as a malignant or benign tumor, and one of the signs is just the fractal dimension of the nuclei of the tumor cells. Under the cat you will find an explanation of the meaning of the fractal dimension of the set, as far as possible in accessible language, an algorithm for calculating the approximate value of this dimension, its implementation in c # and a number of examples with pictures. Perhaps you opened this post just because of the image on the right, I borrowed this image from Jennifer Selter 's instagram , and at the end we will calculate the fractal dimension, so to speak, of the Jennifer filet. I would like to ask you to answer a couple of questions at the end of the post.

Dimension

')
As usual, in order to understand the meaning of the algorithm, you need to plunge into theory. Wikipedia tells us that the dimension in physics (and most likely most people perceive the meaning of dimension in this way) is the number of independent parameters needed to describe the state of an object, or the number of degrees of freedom of a physical system. But in mathematics, everything is a little different, here we have a number of definitions of dimension, which often depend on the working space. Within the framework of the general topology, several definitions of the dimension are given, and of them we will be interested in the Hausdorff dimension, the Minkowski dimension and the fractal dimension .

To begin, let us recall the formal meaning of those dimensions that are intuitive for us, in the vector space that surrounds us. By the basis of a vector space, we mean the maximum set of linearly independent vectors. The number of these vectors we call the dimension of the vector space, or its rank. And any element of a vector space can be represented as a linear combination of basis vectors.

Hausdorff dimension

The Hausdorff dimension generalizes the concept of the dimension of a real vector space, and is a natural way to determine the dimension of a subset in a metric space. For example, the Hausdorff dimension of an n- dimensional (dimension in the sense of a vector space) unitary space (a special case of a vector space) will also be equal to n . A good mathematical description of the Hausdorff dimension is given in the Russian Wikipedia ; it is also important for us to understand the meaning of this dimension intuitively. We represent the complete coverage of a set X by balls of radius at most r , denote the number of these balls by N (r) .



The value of N (r) will increase with decreasing r (more and more balls will be required for full coverage). The Hausdorff dimension of a good set X will be such a unique number d that N (r) will grow as 1 / r ^d as r tends to zero. A good set is understood to be smooth sets without features, such as fractals, for example. Examples of good sets can be any idealized geometric objects such as a cube, a sphere, and so on.

Fractal dimension

We describe one simple way of defining the fractal dimension, although for example the Minkowski dimension is also one of the fractal dimensions, and it is closely related to the Hausdorff dimension, but more on that later. Here it is a simple way to set the fractal dimension:

• Take some D -dimensional geometric structure and iteratively divide its sides into M equal parts (in the next iteration, we divide each part obtained in the previous iteration into M parts as well)
• Each level will consist of M ^D parts of the previous level.
• Denote as follows the number of parts obtained N = M ^D

Perform the following transformation to calculate the formula for the value of the fractal dimension D :



Let's look at simple examples that I learned from a very steep course in complex systems . Take a segment (one-dimensional bounded set), divide it into two equal parts, in the same way we will deal with each received part. In this way, we will create a full set coverage.



Those. M = 2 and N = 2 , since from each part two new pieces of the segment are produced, we calculate D :



If we divide the segment not into 2 parts, but into 3, then D will still be equal to 1, since M = 3 and N = 3 . This dimension coincides with the Hausdorff dimension for a good set.

Let's look at a similar procedure for a square.



We get M = 2 and N = 4 , since dividing the sides into 2 equal parts, we get 4 new ones, we calculate the fractal dimension



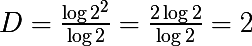
And again, the obtained dimension coincided with the Hausdorff dimension. The same result can be obtained if the sides are divided into 3 equal parts, etc.

Benoit Mandelbrot in the study of real objects made the obvious remark:

it’s not a smooth line

In the real world, we rarely deal with idealized objects, what will happen if we consider a not-quite-good geometric object, such as the Koch curve (not to be confused with a stick), let us recall the algorithm for generating such a set. At each iteration, each piece of the curve, which is a straight segment, is divided into three equal parts, then the middle piece is removed, and in its place becomes a structure resembling an inverted letter V , each edge of which is equal to the removed part of the segment (as well as the remaining ).



In other words, M = 3 , since the segment is divided into three equal parts, and N = 4 , since each part is converted into 4 parts equal to 1/4 of the original. Then the fractal dimension of such a set at infinite iteration will be equal to the following value:



As another example, let's look at the Sierpinski triangle.



At each iteration, one side is divided into 2 parts, i.e. M = 2 , and the result is 3 parts, i.e. N = 3 , then



Of course, the question arises, so we got some numbers, well, the dimension became fractional, so what? Does this make any sense, or is it just math stuff. There is no strict wording describing the meaning of fractionality of dimensionality, but it can be interpreted as follows, at some intuitive level. Fractal dimension is sensitive

to all kinds of imperfections of real objects, allowing us to distinguish and individualize what was previously impersonal and indistinguishable ( source )

The following interpretation is mentioned in the course on the analysis of complex systems: fractional dimension is a kind of self-similarity density .

But speaking about real objects, the reader will immediately say, but then the Koch curve and the Sierpinski triangle are far from reality, what to do then? As I mentioned above, the above definition of fractal dimension is simple, and one of several. Let's move on to a more complex definition of fractal dimension. In the meantime, take a look, for example, at Romanesco broccoli, this is the reality.

Minkowski dimension

The Minkowski dimension is one of the ways of defining the fractal dimension of a bounded set in a metric space, defined as follows:

• where N (ε) is the minimum number of sets of diameter ε with which you can cover the original set.

If the limit does not exist, then consider the upper and lower limits, and say, respectively, of the upper and lower dimensions of Minkowski. The upper and lower Minkowski dimensions are closely related to the Hausdorff dimension, intuitively it is easy to grasp by the way the dimension is specified. Usually the three dimensions mentioned coincide, and only in very specific cases it makes sense to distinguish them, but these are not our cases.

The Minkowski dimension also has another name - the box-counting dimension , due to the alternative method of its definition, which by the way gives a hint to the method of calculating this dimension itself. Consider the two-dimensional case, although a similar definition extends to the n-dimensional case. Take a bounded set in a metric space, for example, a black and white picture, draw a uniform grid with a step ε on it, and paint over those grid cells that contain at least one element of the desired set.



Next, we begin to reduce the size of the cells, i.e. ε , then the Minkowski dimension will be calculated using the above formula, examining the rate of change of the ratio of logarithms. This phrase may not be immediately clear, but I think it will be clarified by the algorithm used to calculate the approximate value of the Minkowski dimension.

Box-counting algorithm

The algorithm is derived as follows; for D _bc , we denote the approximate value of the Minkowski dimension. We write the definition of this dimension, removing the limit, we will simulate it in iterations, in which the size of the cells will change.



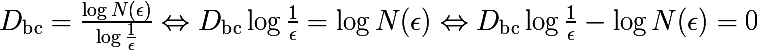
If we fix the cell sizes ε and treat D _bc as unknown, it is easy to see that the expression given is a line formula. We can start a cycle on various cell sizes ε and record the result. Let's plot these results and plot the regression line for the obtained set of data, this value will be an approximation of the fractal dimension of Minkowski.



Here is the way a list of objects with their fractal dimensions .

I hope I managed to convey the connection between the natural dimension, and the way and why people came to different definitions of dimension. Let's go to the code, and then to the examples.

Box-counting algorithm, C # code

To calculate the Minkowski dimension, we will need two procedures, starting with linear regression. In general, the linear regression problem can be solved in various ways; most often, the gradient descent method and the least squares method are used for this (Normal equations). The first works well on large and wide data, the second is weak on wide data because of the need to calculate the inverse matrix, whose width is equal to the width of the data array. In our case, the width is only 2, so this is our case. In vectorized form, the linear regression solution is written as follows:



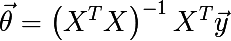
The inverse matrix will be searched by the following formula:





The zero element of the output vector contains the angular coefficient (this will be the desired Minkowski dimension), and the next element is the offset. And actually key function which returns dataset on which it is necessary to calculate the angular coefficient



It remains only to link the two procedures:

 IDictionary<double, double> baList = BowCountingDimension(bwContour, 5, 100, 1, dir + "boxing\\"); double[] y = new double[baList.Count]; double[] x = new double[baList.Count]; int c = 0; foreach (double key in baList.Keys) { y[c] = baList[key]; x[c] = key; c++; } double[] theta = NormalEquations2d(y, x); 

Examples

Letter

Consider a simple image without features , i.e. with smooth edges. In computer vision, it is often not the entire image that is analyzed, but its outline.







The fractal dimension in the area of ​​the unit tells us that the figure is really without features, and quite smooth.

Curve Koch

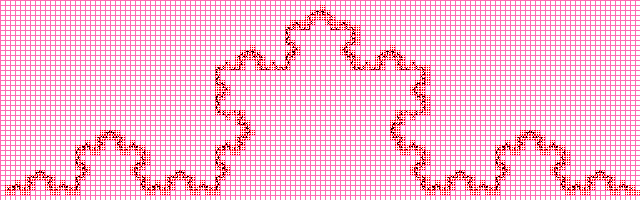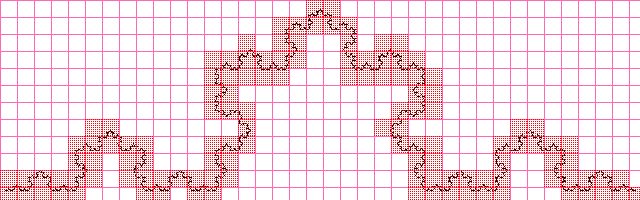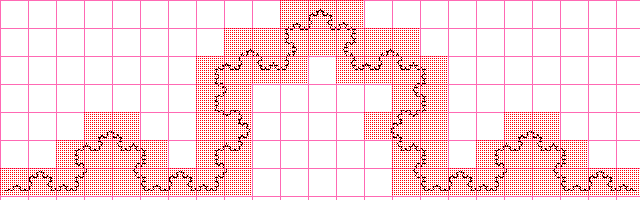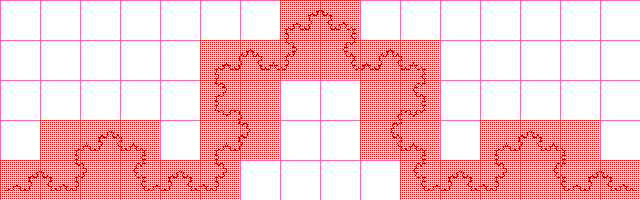
The value is almost the same as when calculating the fractal dimension analytically, it is obvious that with increasing image resolution, the approximated value will approach the calculated one analytically.

JanSetler

Map of Russia

Take something more rugged, such as a map of our country.







It turns out that the priest Jennifer is a little more interesting than the contour of Russia, so what can we do.

Fractal

Will there be a significant difference in the value of the dimension for the fractal? Let's check. Consider one of the sets of Julia , or rather its boundary. Gifku had to cut, because the program did not cope with high resolution, and scaling overwritten the grid.







As you can see, the fractal is even more interesting than the priest Jennifer.

Links

You will find all the information on the links above, at the end I will repeat only about two courses, the second by the way started only a couple of days ago, so I advise everyone.

• Introduction to Complexity
• Introduction to Dynamical Systems and Chaos

As I sent a letter to the Habr’s administrators with a request to create a machine learning hub, I received the following answer: “If there are 15-20 posts that simply have to be in this hub, we will think.” In general, there are more than 15-20 such posts for a long time, I have only a minimum of 10 of them. I understand that the administration is more busy with hubs and politicians, but we can try to draw their attention to really important hubs.