As Robert Morris on 8 bits to 10,000 counted

As everyone knows with the help of n-bit, you can implement a counter counting up to 2 ⁿ -1, but if you have very limited resources, or you just want to experiment and combine into a single sequence, probability, randomness and increase in the counter, then please .


')



In this article we will see how the so-called probability counter works.
He was first introduced by Robert Morris in 1977, a coder working at BellLabs, famous for his phrase

"Three golden rules for computer security: do not own a computer, do not turn it on, and do not use it."

Read more about the meter

We have t bits at our disposal.
Choose a nonnegative ascending sequence n _i (i lies in the range from 0 to 2 ^t - 1), going a little ahead, I will say that the values ​​of n _i will be our counter values.
Now the most interesting thing is that the addition of a counter to 1 occurs with a probability of 1 / (n _{i + 1} - n _i )



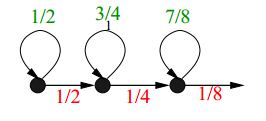
For example, our sequence is n _i = i ² , then increasing the counter from the value of 8 will come true with a probability of 1 / (16-8) = 0.125, as a result, the counter from n _i to n _{i + 1} will increase on average just over n _{i + 1} - n _i operations

A special case of a probabilistic counter is n _i = i, it is obvious that with such a sequence the counter will be normal and the probability of adding it will be equal to 1

Implementation

Now we will try to implement it in practice.
We will implement it in java.
Suppose that we have only 8-bit byte constant memory. Since it is a landmark, with it you can keep up to 127, but this is not enough for us.
The question is what sequence to use. Her choice depends on how much you need to keep a counter and how much you are willing to sacrifice accuracy. At your disposal any integer increasing sequences, for example, you can search them in the Online encyclopedia of sequences .
We will use Fibonacci numbers and squares of numbers .

We will have two main functions. The first one will increment the counter, the second one will return the i-th number of the sequence.

private byte counter = 0; public void increase(){ Random rand = new Random(); int randNumber = rand.nextInt(getElementSequence(counter + 1) - getElementSequence(counter)); if(randNumber == 0) counter++; } 

Here is an increase in the counter, depending on the probability. The counter knows nothing about the sequence and only returns the i-th element, depending on the success or failure of the event.

Here is a sequence of squares of numbers.

 private int getElementSequence(int number){ return (int) Math.pow(number, 2); } 

But from the Fibonacci numbers

  private int getElementSequence(int number){ int sumFib = 1; int previousElement = 0; int temp; for(int i = 0; i < number + 1; i++){ temp = sumFib; sumFib = sumFib + previousElement; previousElement = temp; } return sumFib; } 

We emulate incrementing the counter in a normal loop, suppose in 10,000 iterations.

 public static void main(String[] args) { TestApproximateCounting test = new TestApproximateCounting(); for(int i=0; i<10000; i++){ test.increase(); }; } 

Let's sum up

for each of the sequences I spent on 10 counter runs of 10,000 iterations

Run number	counter value for squares of numbers	Squares of numbers	counter value for Fibonacci numbers	fibonacci numbers
one	93	8,649	20	6,765
2	111	12,321	20	6,765
3	105	11,025	20	6,765
four	103	10,609	21	10,946
five	96	9,216	21	10,946
6	94	8,836	22	17,711
7	93	8,639	nineteen	4 181
eight	106	11,236	nineteen	4 181
9	104	10,816	21	10,946
ten	94	8,836	20	6,765

As you can see, the errors are quite tangible, but if you need to count to more than 10,000 on 8 bits, then a probability counter is a good option.

Literature:
Kormen T., Leyzerson Ch., Rivest R., Stein K. - Algorithms. construction and analysis - 2005
Morris, R. Counting large numbers of events in small registers. Communications of the ACM 21, 10 (1977), 840–842

UPD. Upon request, I added two columns to the table showing the counter values ​​for each of the sequences, but once again I’ll say that the value of the counter itself is not obtained from the counter, but from the getElementSequence function with the counter at the input.