Microsoft's long arithmetic

Introduction

It is known that a computer can operate with numbers, the number of bits of which is limited. As a rule, we are used to working with 32-bit and 64-bit integer numbers, which correspond to the types Int32 (int) and Int64 (long) on ​​the .NET platform, respectively.

And what to do if you need to submit a number, such as, for example, 29! = 8841761993739701954543616000000? This number does not fit in the 64-bit, or even more so 32-bit data type. To work with such large numbers there is a long arithmetic.

Long arithmetic - in computing, operations (addition, multiplication, subtraction, division, exponentiation, etc.) over numbers whose width exceeds the length of the machine word of the given computer. These operations are not implemented in hardware, but in software, using basic hardware to work with numbers of smaller orders.

Long arithmetic can also be considered as one of the sections of olympiad programming, since very often when solving problems, the capacity of standard types is not enough to represent the final result. When choosing a programming language for Olympiad needs, a set of tools built in it (ready-made libraries, implemented classes) is not unimportant. Many languages ​​(Java, Ruby, Python) have built-in support for long arithmetic, which can significantly reduce the time to write a program.
')
The .NET platform up to version 4.0 did not have built-in support for working with long numbers. In the 4th version of .NET, it acquired not only long, but also complex numbers. This functionality is available through the System.Numerics assembly and the BigInteger and Complex types defined in the namespace with the assembly name of the same name.

It should be said that the BigInteger structure should have appeared in .NET 3.5 , but at that time it was not fully ready, its implementation did not meet all needs (this may also include performance problems), so it was decided to postpone its output to .NET 4.0

In this article I would like to consider the details of the implementation of long arithmetic from Microsoft.

General concepts

The idea of ​​representing long numbers in computer memory is quite simple. Consider the number 123456789 in the decimal number system. Obviously, it can be represented as follows:

123456789 ₁₀ = 1 * 10 ⁸ + 2 * 10 ⁷ + 3 * 10 ⁶ + 4 * 10 ⁵ + 5 * 10 ⁴ + 6 * 10 ³ + 7 * 10 ² + 8 * 10 ¹ + 9 * 10 ⁰

In general, any number can be represented as:

A = a _n-1 β ^n-1 + a _n-2 β ^n-2 +… + a ₁ β + a ₀
where β is the base of the number system in which we represent a number, and the coefficients a _i satisfy the double inequality 0 ≤ a _i <β.

The representation of a number resembles the representation of a polynomial, only instead of x to the appropriate degree we have the base β to the necessary degree. As you know, the polynomial a ₀ + a ₁ x + a ₂ x ² + ... + a _n x ^{n is} conveniently represented as an array, whose elements represent the coefficients a _i , and the subscript i defines the corresponding degree x. A long number is stored similarly, it remains to determine the choice of the base β.

For example, the same number 123456789 can be represented in the ten thousandth (β = 10 ⁴ ) number system as follows:

123456789 ₁₀ = 1 * (10 ⁴ ) ² + 2345 * (10 ⁴ ) ¹ + 6789 * (10 ⁴ ) ⁰

Representing the number 123456789 in the ten thousandth number system, we get two advantages at once: first, we reduce the amount of memory consumed, because instead of an array of 9 numbers we only need to store an array of 3 numbers (1, 2345 and 6789), secondly, significantly We reduce the time for performing standard operations on long numbers, since we process 4 digits of a number at a time. In general, a computer equally quickly adds single-digit and 32-bit numbers, so this should be used.

The base of the number system β usually depends on the maximum size of the base data type on the computer, and is selected on the basis of the following considerations:

1. the base must fit one of the basic data types;
2. The base should be as large as possible to reduce the size of the representation of a long number and increase the speed of operations with them, but small enough so that all operations with coefficients use the basic data type;
   
3. for convenience of output and debugging, you can choose β as a degree 10, β - a power of two allows you to perform fast operations at a low level.

It should also be noted that the sign of the number is taken into account in a separate variable, that is, the array contains the modulus of a long number, as well as the number is stored backwards. This is done primarily for convenience: you do not need to process in a special way the zero / last element of the array in which the sign of a number could be stored, as well as all operations are performed from the low order to the high order.

Microsoft BigInteger

If you look at the BigInteger structure through the Reflector decompiler or dotPeek , you will see the following fields:

private static readonly BigInteger s_bnMinInt = new BigInteger(-1, new uint[1]{ (uint) int.MinValue }); private static readonly BigInteger s_bnOneInt = new BigInteger(1); private static readonly BigInteger s_bnZeroInt = new BigInteger(0); private static readonly BigInteger s_bnMinusOneInt = new BigInteger(-1); internal int _sign; internal uint[] _bits; private const int knMaskHighBit = -2147483648; private const uint kuMaskHighBit = 2147483648U; private const int kcbitUint = 32; private const int kcbitUlong = 64; private const int DecimalScaleFactorMask = 16711680; private const int DecimalSignMask = -2147483648; 

The structure contains only two instance fields (_sign and _bits), the remaining fields are constants and static fields for reading representing the structure values ​​for the numbers -1, 0 and 1.

It can be assumed that the _sign variable holds the sign of the number, and the _bits array contains the coefficients a _i . Given that the _bits array is of the type uint [], it can also be assumed that the power of β is taken to be a 2-level 2 ³² (since uint is a 32-bit unsigned number).

So, we will try to confirm or refute our assumptions.

A constructor that takes an int as an argument looks like this:


Its implementation can tell a little more about assigning the _sign variable. As you can see, if a long number is placed in the int range (from -2 ³¹ to 2 ³¹ -1), then it is stored in the _sign variable, and the _bits array is not used, it is null. This optimization should speed up work like BigInteger , as well as reduce the size of memory consumed when the number is not really large.

Go ahead.

A constructor that takes a uint as an argument looks like this:


Depending on whether the number fits in the int range, it is written either in the _sign variable or in the _bits array.

The following constructor accepting a 64-bit number with a (long) sign will help answer the question about choosing the base of the number system:


If the number does not fit into the int range, then, as we see, the _sign variable contains the sign of the number (-1 for negative and 1 for positive), and the _bits array contains those same coefficients a _i and is populated as follows:

 this._bits = new uint[2]; this._bits[0] = (uint) num; this._bits[1] = (uint) (num >> 32); 

In this case, the 64-bit number num is divided into two 32-bit: (uint) num and (uint) (num >> 32). The first number is the last 32 bits of the number num, while the second is the first 32 bits (shifting to the right by n bits is equivalent to integer dividing by 2 ⁿ ).

Let's define how the number will be stored long.MaxValue = 2 ⁶³ -1 = 9223372036854775807 in the structure BigInteger . To do this, divide it by 2 ³² :


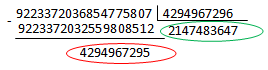
In fact, (uint) long.MaxValue = 4294967295, (uint) (long.MaxValue >> 32) = 2147483647.

This means 9223372036854775807 = 2147483647 * (2 ³² ) ¹ + 4294967295 * (2 ³² ) ⁰ , and BigInteger
will be represented by a pair:

_sign = 1
_bits = {4294967295, 2147483647} // remember that the number is stored backwards

For the long number -1234567891011121314151617181920 we have:



That is, the number is decomposed in powers of 2 ³² as follows:
1234567891011121314151617181920 = 15 * (2 ³² ) ³ + 2501550035 * (2 ³² ) ² + 3243814879 * (2 ³² ) ¹ + 4035623136 * (2 ³² ) ⁰

So, BigInteger will be represented by a pair:

_sign = -1 // number sign
_bits = {4035623136, 3243814879, 2501550035, 15}

A number that fits in the int range, say, 17 will be stored as follows:

_sign = 17
_bits = null

Examining the constructors of the structure BigInteger can be concluded:

1. if the number is placed in the int range, then it is stored in the _sign variable;
2. if the number does not fit into the int range, then its sign is stored in the _sign variable (-1 for negative and 1 for positive), and the _bits array contains the coefficients a _{i of the} long number decomposition with base 2 ³² .

The base β = 2 ³² is a good choice, since it is easier to work at a low level with a power of two (multiplying and dividing by a power of two corresponds to bit shifts left and right), and as many as 32 digits of the number will be processed at a time, which allows you to quickly perform operations on them.

In general, the BigInteger structure is a complete implementation of long arithmetic on the .NET platform. At the same time, Microsoft tried to bring it as close as possible to primitive numeric types: the BigInteger instance can be used just like any other integer type. BigInteger overloads standard numeric operators to perform basic mathematical operations, such as addition, subtraction, division, multiplication, subtraction, negation, and unary negation. You can also use standard numeric operators to compare two BigInteger values ​​with each other. Like other integer types, BigInteger supports the bit operators And, Or, XOR, left shift and right shift.

For languages ​​that do not support custom operators, the BigInteger structure also provides equivalent methods for performing mathematical operations. This applies to the methods Add, Divide, Multiply, Negate, Subtract and some others. Similarly, Microsoft has arrived in the implementation of the Decimal structure.

Many members of the BigInteger structure directly correspond to members of other integer types. In addition, BigInteger adds such elements as:

• IsEven - determines if the number is even;
• IsPowerOfTwo - determines whether the number is a power of two;
• Sign - returns a value indicating the sign of the BigInteger number;
• Abs - returns the absolute value of the number BigInteger;
• DivRem - returns the quotient and the remainder of the division operation;
• GreatestCommonDivisor - returns the greatest common factor for two numbers;
• Log - returns the logarithm of the specified number in the number system with the specified base;
• Max / Min - returns the largest / smallest of two numbers;
• ModPow - performs modular division of a number raised to the power of another number;
• Pow - raises the value of BigInteger to the specified degree.

A few words about BigInteger in Mono and Java

It should be noted that Mono also has the support of long arithmetic. The implementation of the BigInteger structure in Mono is practically no different from the Microsoft implementation, except that there is no optimization for the numbers represented by the int type.

That is, the number 17 in Mono will be represented by a pair:

_sign = 1 // number sign
_bits = {17}

A similar implementation of BigInteger is presented in Java:

 public class BigInteger extends Number implements Comparable<BigInteger> { int signum; int[] mag; private int bitCount = -1; private int bitLength = -1; private int lowestSetBit = -2; private int firstNonzeroByteNum = -2; private int firstNonzeroIntNum = -2; private final static long LONG_MASK = 0xffffffffL; } 

Since Java lacks unsigned types, the mag array is of type int []. Accordingly, the representation of a long number in Java and .NET will be different. In .NET, the presentation will be slightly more efficient, since the uint type covers a larger range:


In Java, as well as in Mono, there is no optimization for numbers represented by the type int.

BigInteger performance

When working with a long number of BigInteger , you need to remember about the potential problems associated with performance. For example, the seemingly innocuous ++ operator can have a significant impact on performance:

 int length = 1000000; BigInteger num = BigInteger.Parse("12345678910111213141516171819"); for (int i = 2; i < length; i++) { if (IsPrime(i)) num++; } Console.WriteLine(num); 

Although it seems that in this example the value of an existing object changes, it is not. BigInteger objects are immutable, that is, internally, the common language runtime actually creates a new BigInteger object and assigns it a value one greater than the previous one.

In this example, you can do the following: perform intermediate operations using ordinary numeric types, and then use BigInteger :

 int length = 1000000; BigInteger num = BigInteger.Parse("12345678910111213141516171819"); int temp = 0; for (int i = 2; i < length; i++) { if (IsPrime(i)) temp++; } num += temp; Console.WriteLine(num); 

Other .NET Framework numeric types are also immutable. However, since the BigInteger type does not have an upper or lower limit, its values ​​can grow to very large values ​​and have a measurable impact on performance.

Instead of conclusion

Summarizing, we can say that the .NET platform, starting with version 4, has acquired a full-fledged implementation of integer long arithmetic. Perhaps, for complete happiness, it remains to implement the structure of BigRational , which has long been present in beta status in .NET BCL.

BigRational structure description : The BigRational structure is based on the BigInteger type that was introduced in the .NET Framework 4 and allows you to create rational numbers of arbitrary precision. A rational number is a ratio of two integers, and in this implementation of the BigRational structure, the BigInteger type is used as the dividend (numerator) and divisor (denominator) type.

Thanks for the remark users: gouranga