Analysis of spherical motion of a solid in the case of Lagrange
This article will tell and show how to apply the Wolfram Mathematica environment to solving complex systems of differential equations, graphical interpretation of the results of the solution, applying procedural programming elements to physical problems, using the example of a rigid body motion. The essence of the article is to show how with the help of computer algebra tools it is easy and simple to analyze complex physical systems that agitated the minds of nineteenth-century physicists.
Spherical movement - the movement of the TT , which has one fixed point. Each of the points of the TT during such movement moves along the surface of the sphere with the center at the point of attachment. In this case, they say about the rotational motion, which is composed of a series of elementary turns around the instantaneous axes of rotation, passing through the point of fixation. The instantaneous axis of rotation continuously changes its position, both with respect to the reference system, in which movement is considered, and in the body itself, thus forming two canonical surfaces, called respectively motionless and mobile axoid.
A TT with a fixed point has 3 degrees of freedom, and its position relative to a given reference frame is determined by three parameters, more precisely, Euler angles. These angles determine the three rotations of the system, which allow you to bring any position of the system to the current one.
If we take the elementary turns of the SC around the Z and X axes in the order Z, X ', Z' 'at the corresponding angles, θ and φ , then this transformation leads to the expression of the rotation matrix through the Euler angles. With the help of such a matrix, TT is rotated in space.

The angles used have the following physical meaning:
The spherical movement of the TT , first described by Leonard Euler (it. Leonhard Euler) has a solution only in three cases:
Further we will talk about the movement of a heavy symmetric top in the case of Lagrange.
Let's build a drawing of a heavy symmetric top in the field of gravity. The role of the top will take a cone.
The equations of motion will be obtained from the kinetic moment theorem, having previously written it in general form in a mobile SC .

Now let us use the drawing we constructed and the theorem we wrote down: omitting the tedious formulas, we take into account the moments of inertia of the symmetric top and, giving similar ones, we obtain the system of equations of motion of the TT in the field of gravity.
This system is not solved strictly analytically, and the solution is presented only in quadratures. We will solve this system numerically and analyze the results obtained.
')
First we need to set the initial conditions for our control system: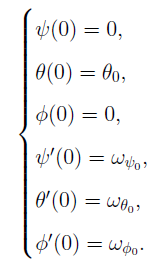
Next, using the capabilities of the computer algebra system, we define the parameters of the top, draw primitives, and solve the system for the remote control numerically.
Then we get the rotation matrix, which we talked about earlier, using the built-in language tools, substitute a numerical solution there and apply the geometric transformation operator to this “cake”:

That's basically the complexity of the solution in a couple of lines. It remains only to define the graphics area, build a motion path and make an animation, but this is already, as they say to an amateur (you can limit yourself to the numerical derivation of transformation matrices). The rest of the code is:
The output of the program results is carried out in the form of a window with dynamic parameters of the initial conditions of the movement, the animation time and the transparency of the top.
Let us analyze the behavior of the top in the case of regular (forced) precession in the field of gravity:
According to the kinetic moment theorem (we talked about it above), for each small time interval dt, the angular momentum vector under the action of gravity increments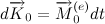 directed along
directed along 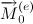 i.e. lying in a horizontal plane perpendicular to the axis of the top. From this it follows that the vector of the angular momentum and, with it, the axis of the gyroscope evenly rotate (perform precession) around the vertical passing through the fulcrum. The top that is inclined to the vertical precess, i.e. in addition to rotating around its own axis, it also rotates around a vertical axis. With fast self-rotation, this precession (rotation around the vertical axis) occurs so slowly that it is possible to neglect with good accuracy that component of the angular momentum, which is caused by the precession around the vertical. This behavior of the top axis is called regular precession. This is a forced precession, as it occurs under the action of the moment of gravity. All points of the top, lying on its axis, move uniformly along circular paths, the centers of which lie on the vertical, passing through the fulcrum of the top. The figure shows an illustration of the regular precession of the top.
i.e. lying in a horizontal plane perpendicular to the axis of the top. From this it follows that the vector of the angular momentum and, with it, the axis of the gyroscope evenly rotate (perform precession) around the vertical passing through the fulcrum. The top that is inclined to the vertical precess, i.e. in addition to rotating around its own axis, it also rotates around a vertical axis. With fast self-rotation, this precession (rotation around the vertical axis) occurs so slowly that it is possible to neglect with good accuracy that component of the angular momentum, which is caused by the precession around the vertical. This behavior of the top axis is called regular precession. This is a forced precession, as it occurs under the action of the moment of gravity. All points of the top, lying on its axis, move uniformly along circular paths, the centers of which lie on the vertical, passing through the fulcrum of the top. The figure shows an illustration of the regular precession of the top.
This event occurs only under strictly defined initial conditions.
Now we can proceed to the study of how the spinning top will behave under the action of gravity under initial conditions that do not provide for the immediate occurrence of regular precession. In general, the movement of the top must be a superposition of forced regular precession and nutation, which is shown in the figure.
At the first moment, as soon as we release the axis of the top, under the action of gravity, it really begins to fall down, which is quite consistent with our intuitive ideas. But as the axis picks up speed, the trajectory of its upper end more and more deviates from the vertical. Soon, the axis movement becomes horizontal, as with regular precession, but the speed of this movement is greater than that needed for regular precession. The trajectory of the end of the axis begins to deviate upwards. Having risen to the initial height, the axis “freezes” - its speed vanishes. Then everything repeats again. But now we understand that such a peculiar behavior, when the end of the axis moves along a cycloidal trajectory, is explained by the addition of two movements — the nutation of the top around the angular momentum vector with the simultaneous forced precession of this vector around the vertical.
When nutations are small, forced precession is called pseudo-regular, in the figure we can observe this phenomenon. For rapidly rotating gyroscopes (that is, very rapidly rotating gyros) used in engineering, the pseudo-regular precession is almost the same as regular precession. In such cases, the nutation manifests itself as a barely noticeable shallow and frequent jitter of the gyroscope axis. In addition, small-scale nutations quickly fade under the action of friction forces, and pseudo-regular precession becomes regular.
Thus, using such a powerful tool as Wolfram Mathematica, we can effortlessly and without knowledge about programming, and most importantly intuitively, as classical textbooks offer, to observe interesting and mysterious processes and phenomena. The main thing is that we can independently spin and rotate any parameters of the system, which is very important for understanding. This project was my term paper, I sat on it a good couple of months, but was pleased with the result. For a long time, I twisted the animation of the movement of my top and played with parameters while observing various trajectories of movement, which Lagrange or Kovalevskaya did not have.
upd. At the request of workers poured the project on DropBox
Used Wolfram Mathematica 9.0
A bit about spherical movement
Spherical movement - the movement of the TT , which has one fixed point. Each of the points of the TT during such movement moves along the surface of the sphere with the center at the point of attachment. In this case, they say about the rotational motion, which is composed of a series of elementary turns around the instantaneous axes of rotation, passing through the point of fixation. The instantaneous axis of rotation continuously changes its position, both with respect to the reference system, in which movement is considered, and in the body itself, thus forming two canonical surfaces, called respectively motionless and mobile axoid.
A TT with a fixed point has 3 degrees of freedom, and its position relative to a given reference frame is determined by three parameters, more precisely, Euler angles. These angles determine the three rotations of the system, which allow you to bring any position of the system to the current one.
Euler angles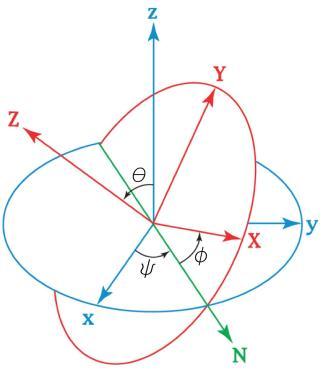

If we take the elementary turns of the SC around the Z and X axes in the order Z, X ', Z' 'at the corresponding angles, θ and φ , then this transformation leads to the expression of the rotation matrix through the Euler angles. With the help of such a matrix, TT is rotated in space.

The angles used have the following physical meaning:
- Angle Ψ - precession angle
- Angle θ - Nutation Angle
- Angle φ - own rotation angle
The spherical movement of the TT , first described by Leonard Euler (it. Leonhard Euler) has a solution only in three cases:
- The case of Euler - the center of mass of the TT , is located at a fixed point. The moment of external forces is zero.
- Lagrange case - TT is dynamically symmetric
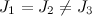 . The center of mass of the TT is on the axis of symmetry.
. The center of mass of the TT is on the axis of symmetry. - The Kovalevskaya case - the body is dynamically symmetric, the moments of inertia are related by
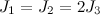 . The center of mass of the TT is in the equatorial plane.
. The center of mass of the TT is in the equatorial plane.
Further we will talk about the movement of a heavy symmetric top in the case of Lagrange.
Equations of motion in the Lagrange case
Let's build a drawing of a heavy symmetric top in the field of gravity. The role of the top will take a cone.
Picture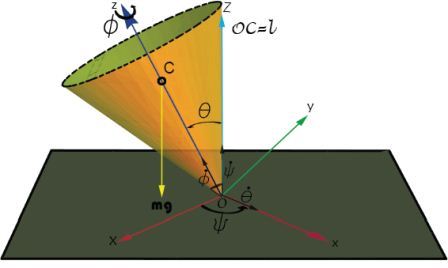

The equations of motion will be obtained from the kinetic moment theorem, having previously written it in general form in a mobile SC .

Now let us use the drawing we constructed and the theorem we wrote down: omitting the tedious formulas, we take into account the moments of inertia of the symmetric top and, giving similar ones, we obtain the system of equations of motion of the TT in the field of gravity.

This system is not solved strictly analytically, and the solution is presented only in quadratures. We will solve this system numerically and analyze the results obtained.
')
Simulation of the Lagrange case in the Wolfram Mathematica system
First we need to set the initial conditions for our control system:
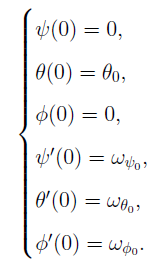
Next, using the capabilities of the computer algebra system, we define the parameters of the top, draw primitives, and solve the system for the remote control numerically.
Code snippets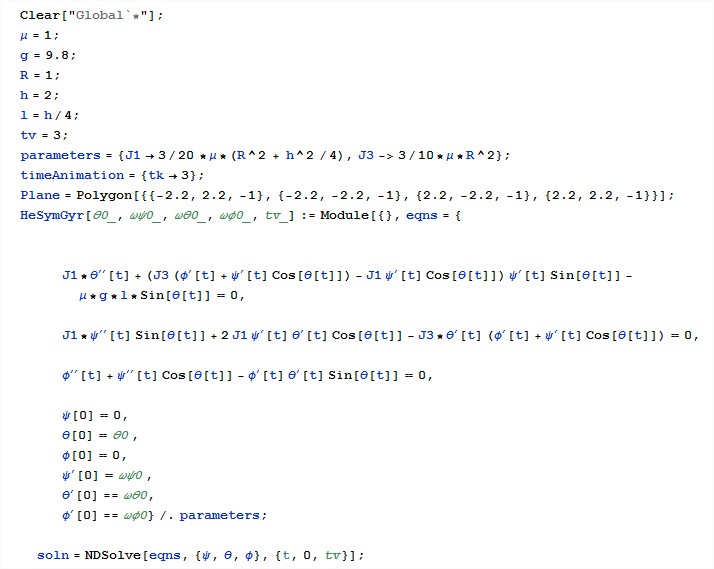

Then we get the rotation matrix, which we talked about earlier, using the built-in language tools, substitute a numerical solution there and apply the geometric transformation operator to this “cake”:

That's basically the complexity of the solution in a couple of lines. It remains only to define the graphics area, build a motion path and make an animation, but this is already, as they say to an amateur (you can limit yourself to the numerical derivation of transformation matrices). The rest of the code is:
Remaining part

Conclusion and analysis of results in the Wolfram Mathematica system
The output of the program results is carried out in the form of a window with dynamic parameters of the initial conditions of the movement, the animation time and the transparency of the top.
Let us analyze the behavior of the top in the case of regular (forced) precession in the field of gravity:
According to the kinetic moment theorem (we talked about it above), for each small time interval dt, the angular momentum vector under the action of gravity increments
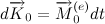 directed along
directed along 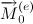 i.e. lying in a horizontal plane perpendicular to the axis of the top. From this it follows that the vector of the angular momentum and, with it, the axis of the gyroscope evenly rotate (perform precession) around the vertical passing through the fulcrum. The top that is inclined to the vertical precess, i.e. in addition to rotating around its own axis, it also rotates around a vertical axis. With fast self-rotation, this precession (rotation around the vertical axis) occurs so slowly that it is possible to neglect with good accuracy that component of the angular momentum, which is caused by the precession around the vertical. This behavior of the top axis is called regular precession. This is a forced precession, as it occurs under the action of the moment of gravity. All points of the top, lying on its axis, move uniformly along circular paths, the centers of which lie on the vertical, passing through the fulcrum of the top. The figure shows an illustration of the regular precession of the top.
i.e. lying in a horizontal plane perpendicular to the axis of the top. From this it follows that the vector of the angular momentum and, with it, the axis of the gyroscope evenly rotate (perform precession) around the vertical passing through the fulcrum. The top that is inclined to the vertical precess, i.e. in addition to rotating around its own axis, it also rotates around a vertical axis. With fast self-rotation, this precession (rotation around the vertical axis) occurs so slowly that it is possible to neglect with good accuracy that component of the angular momentum, which is caused by the precession around the vertical. This behavior of the top axis is called regular precession. This is a forced precession, as it occurs under the action of the moment of gravity. All points of the top, lying on its axis, move uniformly along circular paths, the centers of which lie on the vertical, passing through the fulcrum of the top. The figure shows an illustration of the regular precession of the top.Regular precession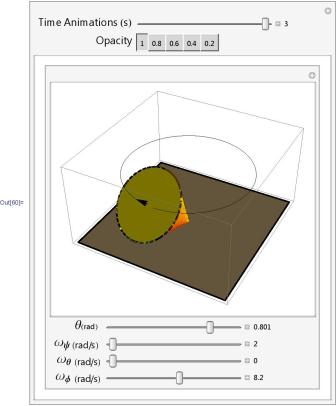

This event occurs only under strictly defined initial conditions.
Now we can proceed to the study of how the spinning top will behave under the action of gravity under initial conditions that do not provide for the immediate occurrence of regular precession. In general, the movement of the top must be a superposition of forced regular precession and nutation, which is shown in the figure.
General case of movement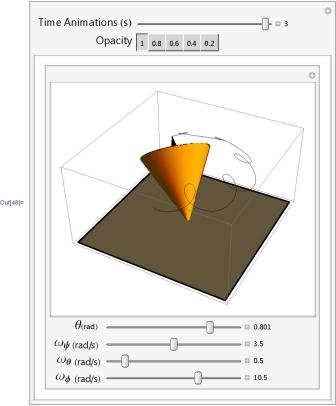

At the first moment, as soon as we release the axis of the top, under the action of gravity, it really begins to fall down, which is quite consistent with our intuitive ideas. But as the axis picks up speed, the trajectory of its upper end more and more deviates from the vertical. Soon, the axis movement becomes horizontal, as with regular precession, but the speed of this movement is greater than that needed for regular precession. The trajectory of the end of the axis begins to deviate upwards. Having risen to the initial height, the axis “freezes” - its speed vanishes. Then everything repeats again. But now we understand that such a peculiar behavior, when the end of the axis moves along a cycloidal trajectory, is explained by the addition of two movements — the nutation of the top around the angular momentum vector with the simultaneous forced precession of this vector around the vertical.
When nutations are small, forced precession is called pseudo-regular, in the figure we can observe this phenomenon. For rapidly rotating gyroscopes (that is, very rapidly rotating gyros) used in engineering, the pseudo-regular precession is almost the same as regular precession. In such cases, the nutation manifests itself as a barely noticeable shallow and frequent jitter of the gyroscope axis. In addition, small-scale nutations quickly fade under the action of friction forces, and pseudo-regular precession becomes regular.
Pseudo-regular precession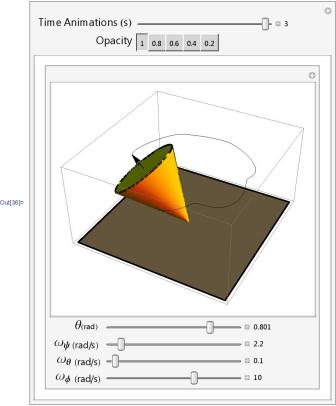

Conclusion
Thus, using such a powerful tool as Wolfram Mathematica, we can effortlessly and without knowledge about programming, and most importantly intuitively, as classical textbooks offer, to observe interesting and mysterious processes and phenomena. The main thing is that we can independently spin and rotate any parameters of the system, which is very important for understanding. This project was my term paper, I sat on it a good couple of months, but was pleased with the result. For a long time, I twisted the animation of the movement of my top and played with parameters while observing various trajectories of movement, which Lagrange or Kovalevskaya did not have.
Literature
- Wittenburg, J. The Dynamics of Systems of Solids / J. Wittenburg.- Moscow: MIR, 1980.-294 p .:
- Rotational motion.
- Euler angles.
- Forced precession of the gyroscope.
upd. At the request of workers poured the project on DropBox
Used Wolfram Mathematica 9.0
Source: https://habr.com/ru/post/207464/
All Articles