Mathematical straightening
In the comments to the previous article “ What the Gantt Chart is silent about or why projects are always late ”, I’ve posted links to videos and slidecasts that describe other reasons causing errors when using Gantt charts. The greatest discussion and misunderstanding caused the straightening of dates due to the asymmetry of the distribution of the deadline for solving the problem. Under the cut is an example of the influence on the end of the project of this very asymmetric distribution.
Before starting, let me remind you that in the framework of the examples given, the values used for solving the problem are taken from some previous experience and are objective. The given examples are designed to demonstrate that based on the construction of a Gantt chart only on the mathematical expectation of the time for the completion of a single task, we will get into trouble.
Consider an example in which the most likely time to solve a problem is 3 hours. It is clear that there is some time faster than that we can not solve the problem. We need to read the task, view the related tasks, discuss some issues with the analyst or architect, open the IDE, download the project, make changes to the code, crash, run, check that everything works as expected, etc. For example, in less than 30 minutes we will not be able to solve the problem. But, on the other hand, if there are problems with a computer (unlikely, but still), when an associated bug is detected, if there is no employee on the spot with whom the task solution needs to be agreed, the period may increase to 6 or even 9 hours. As a result, we obtain the probability distribution density of the form (time on the solution of the problem along the abscis):

And this is not the normal distribution. I, for this article, took the gamma distribution , there are also others, for example, the Maxwell distribution , the beta distribution , etc.
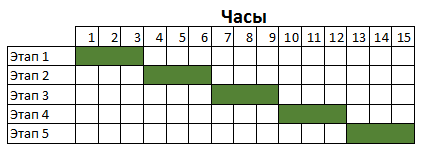
Well, as I said, the mathematical expectation of the time to solve a problem is three hours. Gantt chart for five consecutive tasks will be:
Now let's go back to the gamma distribution and do the calculation or (as I did, I really love programming) modeling the probability of completing all stages at a given hour.
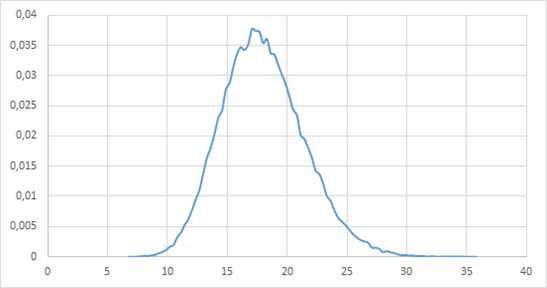
The first news is joyful, the probability distribution density has assumed the form of a normal distribution, but here is the rest ... To understand this rest, we build the probability of completion by the specified hour:
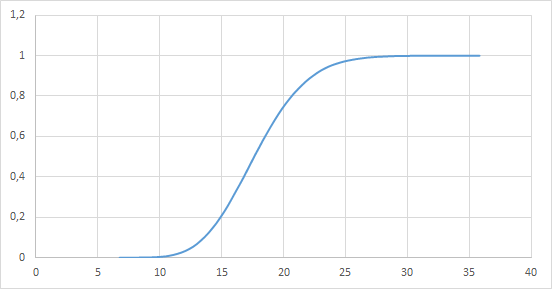
The chance to complete by the scheduled 15 hour is only 20%. To achieve a probability of 90%, you need to shift the completion time by 7 hours (which is 50% of the original time). And then, in the case of the remaining 10%, we will not fit, and with a probability of 5% we will complete these five tasks in 9 hours.
Another sad news is that even the use of the recently popular method of three assessments does not correct the situation much.
If you don’t remember, the main idea of the method of the three estimates is that a pessimistic forecast, an optimistic forecast and a mathematical expectation are taken. In this case, the completion date of the task is determined by the formula:

For our case, if we take the probability of 30% for one task as an optimistic forecast, 95% for a pessimistic forecast and –50% for the most expected one, then, proceeding from the graph of the probability of completing one task by the specified hour:
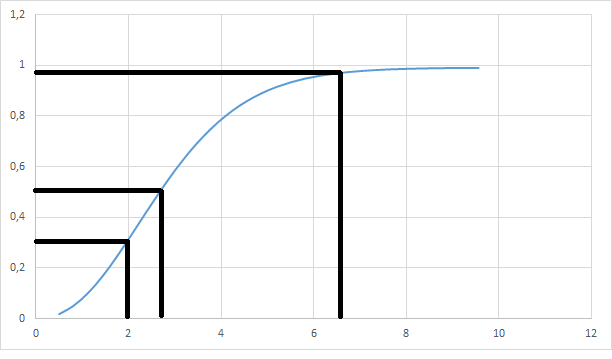
We get that:
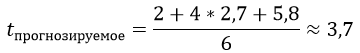
Multiplies 3.7 hours, into 5 stages and we get 18.5 hours. This is already much better, we will fit in this period with a probability of 75%. And in a quarter of cases, we’ll continue the deadlines.
Links to materials from the comments on the previous article:
1. Poisson burning terms
2. Human and Mathematical Straightening
Ps For subtracting and advice on the article a big thanks to Andrei Potapov, CrazyViper and Cartmendum (the last for swearing at my ignorance of the theory of probability).
Before starting, let me remind you that in the framework of the examples given, the values used for solving the problem are taken from some previous experience and are objective. The given examples are designed to demonstrate that based on the construction of a Gantt chart only on the mathematical expectation of the time for the completion of a single task, we will get into trouble.
Consider an example in which the most likely time to solve a problem is 3 hours. It is clear that there is some time faster than that we can not solve the problem. We need to read the task, view the related tasks, discuss some issues with the analyst or architect, open the IDE, download the project, make changes to the code, crash, run, check that everything works as expected, etc. For example, in less than 30 minutes we will not be able to solve the problem. But, on the other hand, if there are problems with a computer (unlikely, but still), when an associated bug is detected, if there is no employee on the spot with whom the task solution needs to be agreed, the period may increase to 6 or even 9 hours. As a result, we obtain the probability distribution density of the form (time on the solution of the problem along the abscis):

And this is not the normal distribution. I, for this article, took the gamma distribution , there are also others, for example, the Maxwell distribution , the beta distribution , etc.
Well, as I said, the mathematical expectation of the time to solve a problem is three hours. Gantt chart for five consecutive tasks will be:

Now let's go back to the gamma distribution and do the calculation or (as I did, I really love programming) modeling the probability of completing all stages at a given hour.

The first news is joyful, the probability distribution density has assumed the form of a normal distribution, but here is the rest ... To understand this rest, we build the probability of completion by the specified hour:

The chance to complete by the scheduled 15 hour is only 20%. To achieve a probability of 90%, you need to shift the completion time by 7 hours (which is 50% of the original time). And then, in the case of the remaining 10%, we will not fit, and with a probability of 5% we will complete these five tasks in 9 hours.
Another sad news is that even the use of the recently popular method of three assessments does not correct the situation much.
If you don’t remember, the main idea of the method of the three estimates is that a pessimistic forecast, an optimistic forecast and a mathematical expectation are taken. In this case, the completion date of the task is determined by the formula:

For our case, if we take the probability of 30% for one task as an optimistic forecast, 95% for a pessimistic forecast and –50% for the most expected one, then, proceeding from the graph of the probability of completing one task by the specified hour:

We get that:
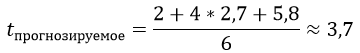
Multiplies 3.7 hours, into 5 stages and we get 18.5 hours. This is already much better, we will fit in this period with a probability of 75%. And in a quarter of cases, we’ll continue the deadlines.
Links to materials from the comments on the previous article:
1. Poisson burning terms
2. Human and Mathematical Straightening
Ps For subtracting and advice on the article a big thanks to Andrei Potapov, CrazyViper and Cartmendum (the last for swearing at my ignorance of the theory of probability).
')
Source: https://habr.com/ru/post/206510/
All Articles