An example of solving a multiple regression problem using Python

Introduction

Good afternoon, dear readers.
In past articles, with practical examples, I have shown how to solve classification problems ( credit scoring task ) and the basics of text information analysis ( passport problem ). Today, I would like to touch on another class of problems, namely the restoration of regression . Tasks of this class, as a rule, are used in forecasting .
For an example of solving a prediction problem, I took the Energy Efficiency dataset from the largest repository UCI . By tradition, we will use Python with the analytical packages pandas and scikit-learn .

Description of the data set and problem statement

A data set is given that describes the following room attributes:

Field	Description	Type of
X1	Relative compactness	Float
X2	Square	Float
X3	Wall area	Float
X4	Ceiling area	Float
X5	Overall height	Float
X6	Orientation	Int
X7	Glazing area	Float
X8	Distributed Glazing Area	Int
y1	Heating load	Float
y2	Cooling load	Float

In him 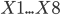- characteristics of the premises on the basis of which the analysis will be conducted, and 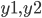- load values ​​that need to be predicted.

Preliminary data analysis

First, let's load our data and look at it:

from pandas import read_csv, DataFrame from sklearn.neighbors import KNeighborsRegressor from sklearn.linear_model import LinearRegression, LogisticRegression from sklearn.svm import SVR from sklearn.ensemble import RandomForestRegressor from sklearn.metrics import r2_score from sklearn.cross_validation import train_test_split dataset = read_csv('EnergyEfficiency/ENB2012_data.csv',';') dataset.head() 

	X1	X2	X3	X4	X5	X6	X7	X8	Y1	Y2
0	0.98	514.5	294.0	110.25	7	2	0	0	15.55	21.33
one	0.98	514.5	294.0	110.25	7	3	0	0	15.55	21.33
2	0.98	514.5	294.0	110.25	7	four	0	0	15.55	21.33
3	0.98	514.5	294.0	110.25	7	five	0	0	15.55	21.33
four	0.90	563.5	318.5	122.50	7	2	0	0	20.84	28.28

Now let's see if there are any attributes related to each other. This can be done by calculating the correlation coefficients for all columns. How to do this was described in a previous article :
')

 dataset.corr() 

	X1	X2	X3	X4	X5	X6	X7	X8	Y1	Y2
X1	1.000000e + 00	-9.919015e-01	-2.037817e-01	-8.688234e-01	8.277473e-01	0.000000	1.283986e-17	1.764620e-17	0.622272	0.634339
X2	-9.919015e-01	1.000000e + 00	1.955016e-01	8.807195e-01	-8.581477e-01	0.000000	1.318356e-16	-3.558613e-16	-0.658120	-0.672999
X3	-2.037817e-01	1.955016e-01	1.000000e + 00	-2.923165e-01	2.809757e-01	0.000000	-7.969726e-19	0.000000e + 00	0.455671	0.427117
X4	-8.688234e-01	8.807195e-01	-2.923165e-01	1.000000e + 00	-9.725122e-01	0.000000	-1.381805e-16	-1.079129e-16	-0.861828	-0.862547
X5	8.277473e-01	-8.581477e-01	2.809757e-01	-9.725122e-01	1.000000e + 00	0.000000	1.861418e-18	0.000000e + 00	0.889431	0.895785
X6	0.000000e + 00	0.000000e + 00	0.000000e + 00	0.000000e + 00	0.000000e + 00	1.000000	0.000000e + 00	0.000000e + 00	-0.002587	0.014290
X7	1.283986e-17	1.318356e-16	-7.969726e-19	-1.381805e-16	1.861418e-18	0.000000	1.000000e + 00	2.129642e-01	0.269841	0.207505
X8	1.764620e-17	-3.558613e-16	0.000000e + 00	-1.079129e-16	0.000000e + 00	0.000000	2.129642e-01	1.000000e + 00	0.087368	0.050525
Y1	6.222722e-01	-6.581202e-01	4.556712e-01	-8.618283e-01	8.894307e-01	-0.002587	2.698410e-01	8.736759e-02	1.000000	0.975862
Y2	6.343391e-01	-6.729989e-01	4.271170e-01	-8.625466e-01	8.957852e-01	0.014290	2.075050e-01	5.052512e-02	0.975862	1.000000

As can be seen from our matrix, the following columns correlate with each other (The value of the correlation coefficient is greater than 95%):

• y1 -> y2
• x1 -> x2
• x4 -> x5

Now let's choose which columns of our pairs we can remove from our sample. To do this, in each pair, select the columns that have a greater impact on the predicted values ​​of Y1 and Y2 and leave them, and remove the rest.
As you can see, the matrices with the correlation coefficients on y1 , y2 have more values X2 and X5 than X1 and X4, so we can delete the last columns we can.

 dataset = dataset.drop(['X1','X4'], axis=1) dataset.head() 

In addition, it can be noted that the fields Y1 and Y2 are very closely correlated with each other. But, since we need to predict both values, we leave them "as is".

Model selection

We separate the predicted values ​​from our sample:

 trg = dataset[['Y1','Y2']] trn = dataset.drop(['Y1','Y2'], axis=1) 

After processing the data, you can proceed to the construction of the model. To build the model we will use the following methods:

• Least square method
• Random forest
• Logistic regression
• Support Vector Machine
• Nearest Neighbor Method

The theory of these methods can be read in the course of KV Vorontsov’s machine learning lectures .
We will estimate using the coefficient of determination ( R-square ). This ratio is defined as follows:



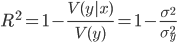
where 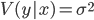- conditional variance of the dependent quantity y by the factor x .
Coefficient takes on the interval and the closer it is to 1, the stronger the dependence.
Well, now you can go directly to building a model and choosing a model. Let's put all our models in one list for the convenience of further analysis:

  models = [LinearRegression(), #    RandomForestRegressor(n_estimators=100, max_features ='sqrt'), #   KNeighborsRegressor(n_neighbors=6), #    SVR(kernel='linear'), #       LogisticRegression() #   ] 

So the models are ready, now we will break our initial data into 2 subsamples: test and training . Who read my previous articles knows that this can be done with the help of the train_test_split () function from the scikit-learn package:

 Xtrn, Xtest, Ytrn, Ytest = train_test_split(trn, trg, test_size=0.4) 

Now, since we need to predict 2 parameters 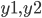, it is necessary to build a regression for each of them. In addition, for further analysis, you can record the results in a temporary DataFrame . You can do it like this:

  #   TestModels = DataFrame() tmp = {} #     for model in models: #   m = str(model) tmp['Model'] = m[:m.index('(')] #     for i in xrange(Ytrn.shape[1]): #  model.fit(Xtrn, Ytrn[:,i]) #   tmp['R2_Y%s'%str(i+1)] = r2_score(Ytest[:,0], model.predict(Xtest)) #    DataFrame TestModels = TestModels.append([tmp]) #     TestModels.set_index('Model', inplace=True) 

As you can see from the code above, to calculate the coefficient 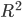r2_score () function is used.
So, the data for the analysis are received. Let's now build the graphics and see which model showed the best result:

 fig, axes = plt.subplots(ncols=2, figsize=(10,4)) TestModels.R2_Y1.plot(ax=axes[0], kind='bar', title='R2_Y1') TestModels.R2_Y2.plot(ax=axes[1], kind='bar', color='green', title='R2_Y2') 

Analysis of the results and conclusions

From the graphs above, we can conclude that the RandomForest method (random forest) did the job better than others. Its coefficients of determination are higher than the others in both variables:
For further analysis, let's re-train our model:

 model = models[1] model.fit(Xtrn, Ytrn) 

Upon careful consideration, the question may arise as to why the dependent sample Ytrn was divided into variables (by columns) the previous time, and now we are not doing this.
The fact is that some methods, such as RandomForestRegressor , can work with several predictable variables, while others (for example, SVR ) can work with only one variable. Therefore, in the previous training, we used partitioning by columns to avoid errors in the process of constructing some models.
To choose a model is, of course, good, but it would also be nice to have information on how each factor influences the predicted value. For this, the model has a property feature_importances_ .
With it, you can see the weight of each factor in the final models:

 model.feature_importances_ 

array ([0.40717901, 0.11394948, 0.34984766, 0.00751686, 0.09158358,
0.02992342])

In our case, it can be seen that the total height and area affect the load most of all during heating and cooling. Their total contribution to the predictive model is about 72%.
It should also be noted that according to the above scheme, it is possible to look at the influence of each factor separately on heating and separately on cooling, but since these factors are very closely correlated with each other ( ), we made a general conclusion on both of them which was written above.

Conclusion

In the article, I tried to show the main stages in regression analysis of data using Python and analytic packages pandas and scikit-learn .
It should be noted that the data set was specially chosen so as to be as formalized as possible and the initial processing of the input data would be minimal. In my opinion, the article will be useful for those who are just starting their way in data analysis, as well as for those who have a good theoretical base, but choose tools for work.