Introduction

In my previous article on non-teacher machine learning methods, the basic algorithm SOINN , an algorithm for constructing self-organizing growing neural networks, was considered. As noted, the basic model of the SOINN network has a number of drawbacks that do not allow it to be used for learning in the lifetime mode (ie, for learning during the whole lifetime of the network). These shortcomings included a two-layer network structure that required, with minor changes in the first layer of the network, retrain the second layer completely. The algorithm also had many customizable parameters, which made it difficult to use when working with real data.

This article will discuss the An Enhanced Self-Organizing Incremental Neural Network algorithm, which is an extension of the basic SOINN model and partially solves the voiced problems.

General idea of ​​SOINN class algorithms

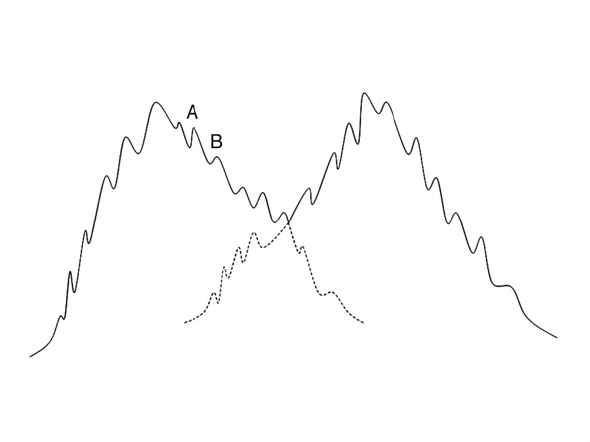
The main idea of ​​all SOINN algorithms is to build a probabilistic data model based on the images provided to the system. In the process of learning, SOINN class algorithms build a graph, each vertex of which lies in the region of the local maximum of the probability density, and the edges connect the vertices belonging to the same classes. The meaning of this approach is to assume that the classes form regions of high probability density in space, and we are trying to construct a graph that most accurately describes such regions and their mutual arrangement. In the best way this idea can be illustrated as follows:

1) For incoming input data, a graph is constructed so that the vertices fall in the region of the local maximum of the probability density. So we get a graph, for each vertex of which we can construct some function that describes the distribution of input data in the corresponding region of space.

2) The graph as a whole is a mixture of distributions, by analyzing which, you can determine the number of classes in the source data, their spatial distribution, and other characteristics.

')

ESOINN Algorithm

We now turn to the consideration of the algorithm ESOINN. As mentioned earlier, the ESOINN algorithm is derived from the basic learning algorithm for self-organizing growing neural networks. Like the basic SOINN algorithm, the algorithm in question is intended for online (and even lifetime) learning without a teacher and without the ultimate goal of learning. The main difference between ESOINN and the algorithm considered earlier is that the network structure is single-layered here and, as a result, has a smaller number of tunable parameters and greater flexibility in learning during the entire operation time of the algorithm. Also, in contrast to the basic network, where the winning nodes were always connected by an edge, a condition for creating a connection appeared in the extended algorithm, taking into account the mutual arrangement of the classes to which the winning nodes belong. The addition of such a rule allowed the algorithm to successfully separate the close and partially overlapping classes. Thus, the ESOINN algorithm attempts to solve the problems identified by the basic SOINN algorithm.

Further, the algorithm for constructing the ESOINN network will be considered in detail.

Flow chart

Algorithm Description

Used notation

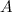- a set of graph nodes.
- set of graph edges.
- number of nodes in .
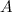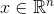- feature vector of the object submitted to the input of the algorithm.
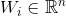- vector of signs of the i-th vertex of the graph.
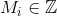- the number of accumulated signals of the i-th vertex of the graph.
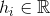- density at the i-th vertex of the graph.

Algorithm

1. Initialize a set of nodes 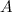two nodes with feature vectors taken randomly from the range of acceptable values.
   Initialize a set of links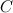 empty set.
   
2. Submit the input feature feature vector to the input. .
   
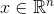3. Find the nearest node (winner) and second closest knot (second winner) like:
   
   
   
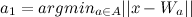
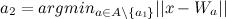
4. If the distance between the feature vector of the input object and or greater than some predetermined threshold or 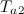, it creates a new node (Add a new node to 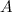and go to step 2).
   and 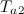calculated by the formulas:
   (if the top has neighbors)
   (if the top has no neighbors)
   
5. Increase the age of all edges emanating from by 1.
   
6. Using Algorithm 2 , determine if a connection is needed between and :
   
   1. If necessary: ​​if edge exists, then reset its age, otherwise create an edge and set its age to 0.
      
   2. If this is not necessary: ​​if the edge exists, then delete it.
      
   
   
7. Increase the number of signals accumulated by the winner according to the formula: .
   
8. Update the winner’s density using the formula: 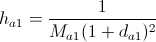where 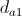- the average distance between nodes within the cluster to which the winner belongs. It is calculated by the formula: .
   
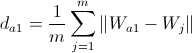9. Adapt the vector of signs of the winner and its topological neighbors with weights and 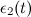by the formulas: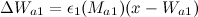
   
   
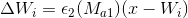
   We use the same adaptation scheme as in the basic SOINN algorithm:
   
   
   
10. Find and remove those edges whose age exceeds a certain threshold value. .
    
11. If the number of input signals generated so far is a multiple of some parameter , then:
    
    1. Update class labels for all nodes using Algorithm 1 .
       
    2. Remove the nodes that are noise, as follows:
       
       1. For all nodes of : if a node has two neighbors and 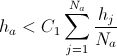, then delete this node.
          
       2. For all nodes of : if the node has one neighbor and 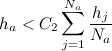, then delete this node.
          
       3. For all nodes of : if the node has no neighbors, then delete it.
          
       
       
    
    
12. If the learning process is completed, then classify the nodes of different classes (using the algorithm for selecting related components of the graph), then report the number of classes, the prototype vector for each class, and stop the learning process.
    
13. Go to step 2 to continue learning without a teacher if the learning process is not finished yet.
    

Algorithm 1: Division of the composite class into subclasses

1. A node is called a vertex of a class if it has the maximum density in a neighborhood. Find all such vertices in the composite class and assign them different labels.
   
2. Assign the remaining vertices to the same classes as the corresponding vertices.
   
3. Nodes lie in the area of ​​overlapping classes, if they belong to different classes and have a common edge.
   

In practice, this method of class division into subclasses leads to the fact that in the presence of noise a large class can be falsely classified as several small classes. Therefore, before you divide the classes, you need to smooth them.

Suppose we have two unsmootted classes:

Take a subclass 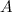and subclass 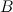. Suppose the vertex density of a subclass 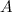equals , and have a subclass 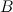equals 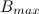. Combine 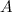and 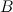in one subclass if the following conditions are met: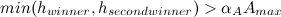

or

Here, the first and second winners are in the area of ​​overlapping subclasses. 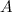and 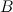. Parameter is calculated as follows: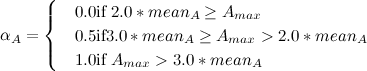
where - average density of nodes in a subclass .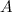

After that, remove all edges connecting vertices of different classes. Thus, we divide the composite class into subclasses that do not overlap.

Algorithm 2: Building a connection between vertices

Connect two nodes in the event that:

1. At least one of them is a new node (it is not yet determined to which subclass it belongs).
   
2. They belong to the same class.
   
3. They belong to different classes, and the conditions for the merging of these classes are fulfilled (conditions from Algorithm 1 ).
   

Otherwise we do not connect these nodes, and if the connection between them exists, then we delete it.

By using Algorithm 1 when checking the need to create an edge between nodes, the ESOINN algorithm will try to find a “balance” between unnecessary class separation and combining different classes into one. This property allows successful clustering of closely spaced classes.

Algorithm Discussion

Using the algorithm shown above, we first find a pair of vertices with the feature vectors closest to the input signal. Then we decide whether the input signal belongs to one of the already known classes or is it a representative of a new class. Depending on the answer to this question, we either create a new class on the network, or adjust the already known class corresponding to the input signal. In the event that the learning process lasts quite a long time, the network adjusts its structure, separating the unlike and combining similar subclasses. After the training is completed, we classify all the nodes into different classes.

As you can see, in the course of its work, the network can learn new information, while not forgetting all that it has learned earlier. This property allows to some extent solve the stability-plasticity dilemma and makes the network ESOINN suitable for lifetime education.

Experiments

To conduct experiments with the presented algorithm, it was implemented in C ++ using the Boost Graph Library. The code is posted on GitHub .

A competition for the classification of handwritten numbers based on MNIST, on the website kaggle.com, was used as a platform for experiments. The training data contains 48000 images of handwritten numbers 28x28 pixels in size and having 256 shades of gray, presented in the form of 784-dimensional vectors.

We received the results of the classification in a non-stationary environment (that is, the network continued to learn during the classification of the test sample).

The network parameters were taken as follows:
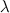= 200
= 50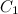
= 0.0001
= 1.0

As a result of the work, the network identified 14 clusters whose centers are as follows:


At the time of this writing, ESOINN occupied an honorable 191 place in the rating with an accuracy of 0.96786 for 25% of the test sample, which is not so bad for an algorithm that initially had no a priori information about the input data.

Conclusion

This article has reviewed a modified learning algorithm for growing ESOINN neural networks. Unlike the basic SOINN algorithm, the ESOINN algorithm has only one layer and can be used for a lifetime of study. Also, the ESOINN algorithm allows working with partially overlapping and fuzzy classes, which the basic version of the algorithm did not know how. The number of algorithm parameters was reduced by half, which makes it easier to configure the network when working with real data. The experiment showed the operability of the considered algorithm.

Literature

1. “An enhanced self-organizing incremental neural network for online unsupervised learning” Shen Furaoa, Tomotaka Ogurab, Osamu Hasegawab, 2007 .
   
2. Osamu Hasegawa from Tokyo Institute of Technology at IIT Bombay.
   
3. Osamu Hasegawa from the Tokyo Institute of Technology at IIT Bombay (video).
   
4. Website of the Hasegawa Lab , which studies self-organizing growing neural networks.