"The problem somehow agreed with the answer!"

I often hear about the work asked from the mostly academic environment, due to the huge amount of calculations performed there: “Why do our results vary from launch to launch of the same application? We do not change anything in it. " It is worth noting that we already talked about this, but only partially answering the question. I will try to tell about this problem a little bit more.

Why we can see the following picture on the same system:


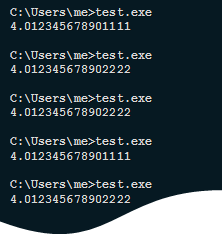
Or, say, the following, on two different machines:
')

The main reason why all this happens is that the law of associativity, which always works in mathematics, is impossible to perform in calculations on machines with a limited bit grid, that is, (a + b) + c is not equal to a + (b + c).
On this topic, many interesting things can be found in the article What Every Computer Scientist Should Be About Floating-Point Arithmetic , by David Goldberg. I will give a simple illustrative example, when in the calculations there are very small and relatively large numbers:


It seems that while everything is expected, if we consider it as mathematics. Now suppose that we work with numbers with single precision, and add a small number with a large one:


From the point of view of machine arithmetic, we obtained the correct result, according to the IEEE 754 standard. And the following result is also true:


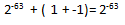
This is where all the problems start to come out. After all, the compiler can quite optimize our code so that the order of additions in expressions will change, and there is a lot more of that. And here will help options –fp-model , about which I have already described in detail.

That's just not everything depends on the compiler. Remember, the original question then sounded so that nothing seemed to change in the code, which means it was not “reassembled”, but the results are still different.

So, other factors come on the scene. For sequential applications, as well as for parallel ones, one of the important aspects for obtaining reproducible results is data alignment. By the way, it also has a huge impact on performance. And if no one has leveled the data in our code, then in cycles that are vectorized, a different number of iterations will be recognized as a prologue, the core of the loop and the epilogue, and, accordingly, the order of calculations will be changed. In order to prevent such problems, you can go two ways:

1) Save the optimization, but explicitly align the data, for example, using _mm_malloc () and _mm_free () . There are directives in FORTRAN ! DIR $ ATTRIBUTES ALIGN: 64 :: arrayname , as well as the compiler option -align array64byte
2) Refuse vectorization of reductions and a number of other optimizations using the –fp-model precise option, which would entail a loss in performance.

Fine! Suppose that we compiled our code with –fp-model precise , but the results are still not consistent. What is wrong now? In fact, there are a number of reasons.

First, if our application is parallel, then this is the number of threads. Say, reductions in OpenMP are in no way affected by the compiler options. Thus, by changing the number of streams, and on different systems it may well be different by default, we implicitly change the order of additions in the reductions (as well as their number). Moreover, no one says that the intermediate amounts in OpenMP will be summed up in the same sequence from start to start, respectively, even with the same number of threads we can get different order of summation, and therefore different results. By the way, this is typical of both icc and gcc. The results may well be more accurate than in the sequential version of the reduction.

We need to control this ourselves, and in the Intel compiler, starting with version 13.0, there is an environment variable that allows deterministic reductions to be performed. This is KMP_DETERMINISTIC_REDUCTION . We set it to yes, and we can be calm, but only if we use the static distribution of work between threads (static scheduling), and the number of threads is constant.
If we use Intel Threading Building Blocks, then there we can control the reductions, through a call to the parallel_deterministic_reduce () function. By the way, Intel TBB is not dependent on the number of threads, and the result may differ from the sequential version of the reduction.

Good. We added this, but again it does not help.
Then there is a suspicion that libraries are used that know not to know about your desire for "permanence." I want to first pay attention to the challenges of mathematical functions. The –fp-model option allows to achieve consistency of function calls, but to get identical results on different architectures (including non-Intel), it is recommended to use the –fimf-arch-consistency key.

A more “powerful” example is the use of the Intel Math Kernel Library, which by default is not focused on reproducible results, but this can be achieved using advanced settings and subject to a number of limitations.

For example, with the same number of threads, a static scheduler (OMP_SCHEDULE = static, set by default), the same OS and architecture, you can get reproducible results. This feature is called MKL Conditional Numerical Reproducibility. I think it is clear why it is conditional. By the way, before, there was also a requirement for data alignment, but in the latest version, the engineers had “nasamaned” something, and this condition can no longer be taken care of when working with the MKL. So, if these requirements are met, setting the environment variable MKL_CBWR_BRANCH (for example, to “COMPATIBLE” ), or calling the function mkl_cbwr_set (MKL_CBWR_COMPATIBLE) in the code, we get the long-awaited “stability”.

Thus, working with a large number of calculations, we should understand that it is possible to achieve "permanent" results, but only with the observance of a number of conditions, which we talked about. In almost all tools today there is a way to control this issue, you need to be careful and set the necessary settings and options. Well, and more - often the reason is trivial, and lies in the usual errors. Sometimes it’s interesting to see code that computes serious scientific formulas using, say, uninitialized variables. And then we wonder why this next rocket flew the wrong way. Be careful when writing code and use the right tools to create and debug it.

By the way, such a question. Why, in the example on systems with different Xeons (picture above), did we get different results? I obviously did not write about it, it would be interesting to hear your ideas.