Math Focus for MP3, JPEG and Homer Simpson
Nine years ago, I attended a physics course in college, and my professor told one thing that struck me. I think it is no exaggeration to say that this is one of the most widely used mathematical discoveries - from optics to quantum physics, radio astronomy, MP3 and JPEG compression, X-ray crystallography, voice recognition and MRI. This mathematical tool is called the Fourier transform, in honor of the 18th century French physicist and mathematician Joseph Fourier. It was even used by James Watson and Francis Crick to decode the DNA double helix structure from radiographs produced by Rosalinda Franklin. (Crick was an expert on Fourier transforms; he jokingly called his book Fourier Transformations for Ornithologists, to explain the essence of Watson, an avid bird lover).
You probably use the Fourier idea every day if you listen to MP3s, watch pictures on the Internet, ask a Siri question, or catch a radio station. (Fourier, by the way, loved working. In addition to his work in the field of theoretical physics and mathematics, he also became the first to discover the greenhouse effect [pdf].)
So what is the Fourier discovery and why is it so useful? Imagine a note on the piano. When you press a piano key, the hammer strikes a string that vibrates at a certain frequency (note A - 440 times per second). As the string vibrates, air molecules around it move back and forth, creating a wave of molecules, which we call sound. If you could observe the movement of air, you would see a smooth, wavy, endlessly repeating curve called a sinusoid. (Explanation: In the piano key example, more than one sinusoid actually occurs. The richness of the real notes of the piano lies in a large number of soft overtones that appear in addition to the main sinusoidal wave. The note is approximately equal to the sinusoid, but with the help of a tuning fork you can get a sound that consists of one sinusoid).
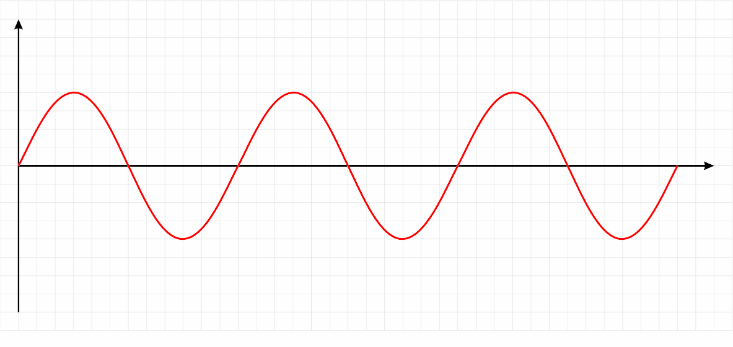
The sound wave of a note can be considered as a simple sine wave. Milan B on the Shuttershock
')
Now press the three keys together to get a chord. The resulting sound wave will not turn out so neat - it will be more erratic. But in this curve of the sound wave is hidden a simple picture. After all, we received a chord by pressing only three keys, so this sound wave consists of three notes (or sinusoids).

The sound wave received by the piano chord may look random, but this is just the sum of three different notes. Christine Daniloff / MIT
Fourier has guessed that this is not just a special property of musical chords, it is applicable in a more general form to any repetitive wave, square, round, wavy, triangular, in general - to any. The Fourier transform is similar to a mathematical prism - you give a wave, but it shows its component parts, that is, notes (or sinusoids), which, when combined, will recreate the wave.
If this sounds a bit abstract, here are some methods for visualizing the Fourier stunt. Here we meet Lucas V. Barbos , a Brazilian physics student who donates incredible mathematical and scientific animations for Wikipedia under the name LucasVB.
So, let's look at the square wave passed through the Fourier prism and see what happened at the output.

Frames from the LucasVB animation
In these pictures (the link above you can see the animation as a whole), the red square wave is converted into a set of notes (blue sine waves). Blue waves are the mathematical ingredients of a red wave. By the same analogy, the Fourier transform is a recipe that will accurately indicate how much and which note must be mixed together to restore the original wave. The vertical blue lines in the animation is a graph that visually represents the amount of each note.
Here is a slightly different approach , presented by Matthew Henderson or "Matthen", a student at Cambridge University, who also creates animations of interesting mathematical pieces . Matthen explains Fourier's trick using circles instead of sinusoids. He comes to the aid of a set of circles of various sizes, the center of each of which is on the border of a larger circle. Circles begin to rotate, small ones move around large and make it faster. If you trace the movement of one point on the smallest circle, you can reconstruct a wave of any shape, as shown in the animation and in the picture. Again, the Fourier transform tells us how to build a wave: which circles and speeds to use.
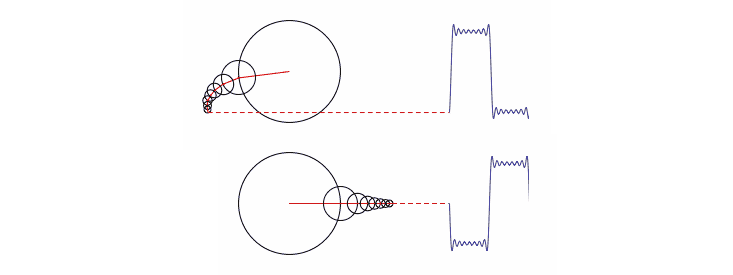
Matthew henderson
If you caught a spirograph , then the idea of tracking complex patterns with the help of circles inside circles may seem familiar to you. This is an interactive version of the animation, similar to that created by LucasVB, where you can have fun and resize circles.
In general, the Fourier transform tells us how much each ingredient of a “note” (sine wave or circle) is contained in a common wave. And this is why it is useful. Imagine that you are talking to your friend on the phone and you want him to draw this square wave. You can use a tedious way and read out a long list of numbers that show the height of the wave at each moment in time. Taking into account all these numbers, your friend will be able to create the original wave. This is how old audio formats worked, for example, WAV. But if your friend understands the Fourier transforms, you can make everything easier: you can just name a few numbers - the sizes of the circles in the picture above. These circles can be used to restore the original wave.
This is not some complicated mathematical trick. Fourier transform is used almost everywhere where there are waves. The ubiquitous MP3 format uses the Fourier stunt version to achieve tremendous compression compared to WAV files (pronounced “wave”) that were before it. MP3 breaks the song into short segments. In each segment, the Fourier transform breaks the audio wave into component notes that are stored instead of the original wave. The Fourier transform also tells us how much and which note is used in the song to know which notes are important. Very high notes are not so important (our ears can barely hear them), so the MP3 throws them away, achieving even greater data compression. Therefore, music lovers do not like MP3 - this is not a lossless audio format, and they claim that they can hear the difference.
The Shazam application recognizes songs in this way. It breaks a song into pieces, and then uses the Fourier transform to determine the notes that make up each piece. It then searches the database to see if this “fingerprint” of the notes resembles any stored songs. Speech recognition uses the same idea to compare notes in your voice with a list of known words.
You can use Fourier transform for images. Here's a great video that shows how you can draw a face of Homer Simpson using circles. Online encyclopedia Wolfram Alpha uses a similar idea to draw the faces of famous people . The following fact is useful to show off knowledge at a party: Fourier transform is also used to compress images into JPEG format. In the good old days of Microsoft Paint, images were saved in BMP format, which was a long list of numbers that encode the color of each pixel. JPEG is an MP3 image. To create a JPEG, you need to divide the image into small squares of 8 by 8 pixels. To recreate the image, for each part you need to apply the same idea of a circle that draws the face of Homer Simpson. Just like MP3s throw very high notes, JPEG drops very small circles. As a result, we get a huge reduction in file size with a small loss of quality, this trick gave us an online world that we all love (and thanks to which we got gifs with cats).

Randall Munroe / XKCD
How are Fourier transforms used in science? Through Twitter, I asked scientists to describe how Fourier's ideas helped them in their work. The answer struck me. The responding scientists used the Fourier transform to study the vibrations of immersed structures interacting with liquids, to predict earthquakes, to determine the components of very distant galaxies, to search for new physical processes in the thermal remnants of the Big Bang, to determine the structure of proteins, to analyze digital NASA signals, for study the acoustics of musical instruments, to refine the model of the water cycle, to search for pulsars (rotating neutron stars) and to determine the structure ry molecules using nuclear magnetic resonance. Fourier transform was even used to identify fake Jackson Pollock paintings through the recognition of chemicals in paint.
Like this! Quite a lot for one mathematical focus.
Aatish Bhatia recently received his Ph.D. in Physics from Princeton University , promoting science and engineering. He is the author of the acclaimed Empirical Zeal blog, tweeter account @ aatishb .
You probably use the Fourier idea every day if you listen to MP3s, watch pictures on the Internet, ask a Siri question, or catch a radio station. (Fourier, by the way, loved working. In addition to his work in the field of theoretical physics and mathematics, he also became the first to discover the greenhouse effect [pdf].)
So what is the Fourier discovery and why is it so useful? Imagine a note on the piano. When you press a piano key, the hammer strikes a string that vibrates at a certain frequency (note A - 440 times per second). As the string vibrates, air molecules around it move back and forth, creating a wave of molecules, which we call sound. If you could observe the movement of air, you would see a smooth, wavy, endlessly repeating curve called a sinusoid. (Explanation: In the piano key example, more than one sinusoid actually occurs. The richness of the real notes of the piano lies in a large number of soft overtones that appear in addition to the main sinusoidal wave. The note is approximately equal to the sinusoid, but with the help of a tuning fork you can get a sound that consists of one sinusoid).

The sound wave of a note can be considered as a simple sine wave. Milan B on the Shuttershock
')
Now press the three keys together to get a chord. The resulting sound wave will not turn out so neat - it will be more erratic. But in this curve of the sound wave is hidden a simple picture. After all, we received a chord by pressing only three keys, so this sound wave consists of three notes (or sinusoids).

The sound wave received by the piano chord may look random, but this is just the sum of three different notes. Christine Daniloff / MIT
Fourier has guessed that this is not just a special property of musical chords, it is applicable in a more general form to any repetitive wave, square, round, wavy, triangular, in general - to any. The Fourier transform is similar to a mathematical prism - you give a wave, but it shows its component parts, that is, notes (or sinusoids), which, when combined, will recreate the wave.
If this sounds a bit abstract, here are some methods for visualizing the Fourier stunt. Here we meet Lucas V. Barbos , a Brazilian physics student who donates incredible mathematical and scientific animations for Wikipedia under the name LucasVB.
So, let's look at the square wave passed through the Fourier prism and see what happened at the output.

Frames from the LucasVB animation
In these pictures (the link above you can see the animation as a whole), the red square wave is converted into a set of notes (blue sine waves). Blue waves are the mathematical ingredients of a red wave. By the same analogy, the Fourier transform is a recipe that will accurately indicate how much and which note must be mixed together to restore the original wave. The vertical blue lines in the animation is a graph that visually represents the amount of each note.
Here is a slightly different approach , presented by Matthew Henderson or "Matthen", a student at Cambridge University, who also creates animations of interesting mathematical pieces . Matthen explains Fourier's trick using circles instead of sinusoids. He comes to the aid of a set of circles of various sizes, the center of each of which is on the border of a larger circle. Circles begin to rotate, small ones move around large and make it faster. If you trace the movement of one point on the smallest circle, you can reconstruct a wave of any shape, as shown in the animation and in the picture. Again, the Fourier transform tells us how to build a wave: which circles and speeds to use.

Matthew henderson
If you caught a spirograph , then the idea of tracking complex patterns with the help of circles inside circles may seem familiar to you. This is an interactive version of the animation, similar to that created by LucasVB, where you can have fun and resize circles.
In general, the Fourier transform tells us how much each ingredient of a “note” (sine wave or circle) is contained in a common wave. And this is why it is useful. Imagine that you are talking to your friend on the phone and you want him to draw this square wave. You can use a tedious way and read out a long list of numbers that show the height of the wave at each moment in time. Taking into account all these numbers, your friend will be able to create the original wave. This is how old audio formats worked, for example, WAV. But if your friend understands the Fourier transforms, you can make everything easier: you can just name a few numbers - the sizes of the circles in the picture above. These circles can be used to restore the original wave.
This is not some complicated mathematical trick. Fourier transform is used almost everywhere where there are waves. The ubiquitous MP3 format uses the Fourier stunt version to achieve tremendous compression compared to WAV files (pronounced “wave”) that were before it. MP3 breaks the song into short segments. In each segment, the Fourier transform breaks the audio wave into component notes that are stored instead of the original wave. The Fourier transform also tells us how much and which note is used in the song to know which notes are important. Very high notes are not so important (our ears can barely hear them), so the MP3 throws them away, achieving even greater data compression. Therefore, music lovers do not like MP3 - this is not a lossless audio format, and they claim that they can hear the difference.
The Shazam application recognizes songs in this way. It breaks a song into pieces, and then uses the Fourier transform to determine the notes that make up each piece. It then searches the database to see if this “fingerprint” of the notes resembles any stored songs. Speech recognition uses the same idea to compare notes in your voice with a list of known words.
You can use Fourier transform for images. Here's a great video that shows how you can draw a face of Homer Simpson using circles. Online encyclopedia Wolfram Alpha uses a similar idea to draw the faces of famous people . The following fact is useful to show off knowledge at a party: Fourier transform is also used to compress images into JPEG format. In the good old days of Microsoft Paint, images were saved in BMP format, which was a long list of numbers that encode the color of each pixel. JPEG is an MP3 image. To create a JPEG, you need to divide the image into small squares of 8 by 8 pixels. To recreate the image, for each part you need to apply the same idea of a circle that draws the face of Homer Simpson. Just like MP3s throw very high notes, JPEG drops very small circles. As a result, we get a huge reduction in file size with a small loss of quality, this trick gave us an online world that we all love (and thanks to which we got gifs with cats).

Randall Munroe / XKCD
How are Fourier transforms used in science? Through Twitter, I asked scientists to describe how Fourier's ideas helped them in their work. The answer struck me. The responding scientists used the Fourier transform to study the vibrations of immersed structures interacting with liquids, to predict earthquakes, to determine the components of very distant galaxies, to search for new physical processes in the thermal remnants of the Big Bang, to determine the structure of proteins, to analyze digital NASA signals, for study the acoustics of musical instruments, to refine the model of the water cycle, to search for pulsars (rotating neutron stars) and to determine the structure ry molecules using nuclear magnetic resonance. Fourier transform was even used to identify fake Jackson Pollock paintings through the recognition of chemicals in paint.
Like this! Quite a lot for one mathematical focus.
Aatish Bhatia recently received his Ph.D. in Physics from Princeton University , promoting science and engineering. He is the author of the acclaimed Empirical Zeal blog, tweeter account @ aatishb .
Source: https://habr.com/ru/post/204956/
All Articles