Solution Zeronights Crackme 2013 and where does the matrix
Hello to all. Recently, an article appeared on Habré describing a crackme from Kaspersky Lab from the ZeroNights 2013 conference. I also managed to crack this crackme, but I used a slightly different approach to creating keys than Darwin, because I noticed that crackme uses matrix operations. Unlike Darwin, I only used debugging with OllyDbg.
Enter random values. Get MessageBox with Fail:

Open the Modules window (large M) in an ollie. Press Ctrl + B (Search). Enter the value fail in the ASCII field. Hit on search - found:
')

Right-click on the first byte of the message, Breakpoit -> Memory -> On Access.
We start debugging. Enter the same values in the crackme fields. We get on passing the MessageBox parameters:
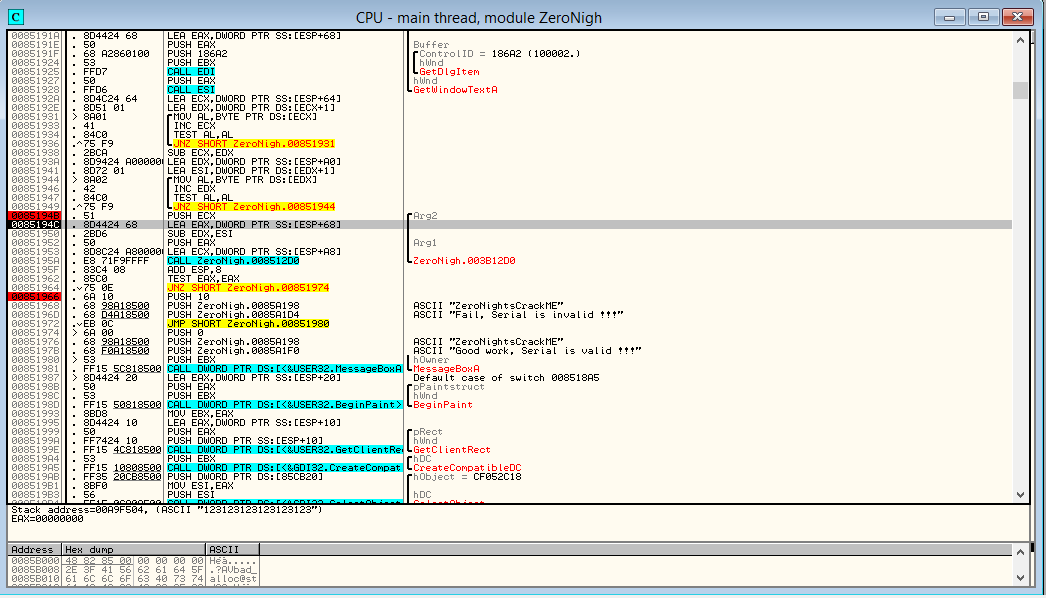
Before push with our line the conditional transition JNZ is visible. Before him TEST EAX, EAX. That is, if EAX is not zero, then MessageBox crashes with the string
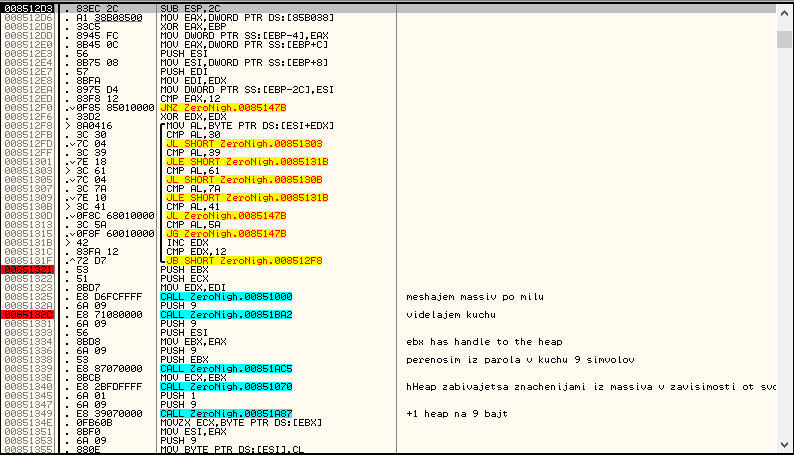
We look at the first JNZ. Before it, the password length is compared with 0x12 (18 in decimal). If not, Fail. Next is the cycle (it is highlighted with a black bracket on the left), in which the password character is checked. They must belong to the sets 0-9, AZ and az. From the comments on the right one can understand that not all functions are important for reverse. Some are simply functions of copying or highlighting arrays and are not of particular interest. The first function after the loop is very important, so we will consider it in detail:
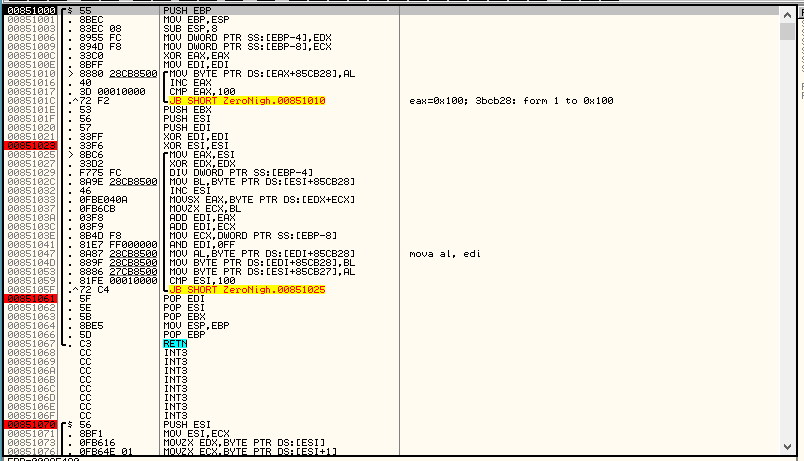
Immediately noticeable two cycles. What happens in them? In the first, we fill the array in memory with values from 0 to 255.
In the second cycle, everything is not so simple. Two pointers are taken: on the array, filled in the first cycle, and on the line with the mail. An array element is taken by the cycle number and a character from the mail by the cycle number modulo the mail length. These bytes are summed modulo 256 (AND AND EDI operation, 0xFF is equivalent to __edi% 0x100 in syntax C). 2 item numbers are obtained in a loop step and received at the expense of mail. These 2 elements are swapped. Mail is the key with which the substitution of elements from 0 to 256 is performed. Simply the array is mixed. We leave from this function back to the general. Next, the array is allocated to 9 bytes and the first 9 characters of the password are copied into it. We will not consider these functions. Let's enter the function with a comment on translit starting with “hHeap zabivajetsa”:
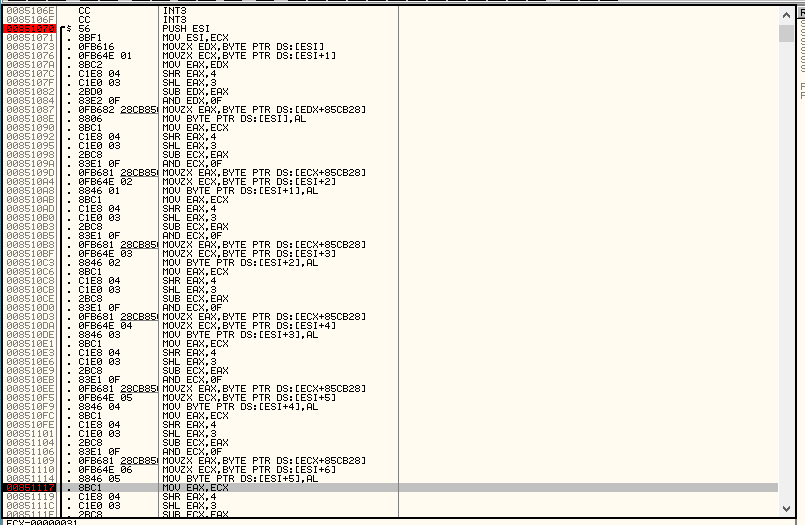
It looks scary, but if you look closely, you can see that the actions are repeated, which means that we have a developed cycle. It is enough to consider only one iteration, everything else is identical.
The first character of the array of 9 bytes is placed in EDX. That is the first character of the password. Further magic:
MOV EAX, EDX
SHR EAX, 4
SHL EAX, 3
SUB EDX, EAX
AND EDX, 0F
In C, it will be:
Replace the password character in hHeap with the value from our mixed array using the EDX number. For the remaining characters is similar. Exit the function.
Another array is allocated for 9 bytes and the values from the first array are transferred to it, but according to certain rules:
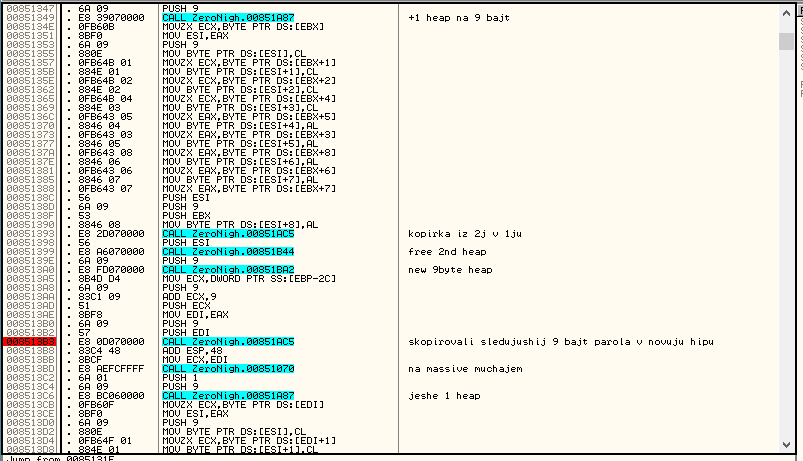
Moving is a block of MOV and MOVZX. Let the first array A, and the second - B. On C:
After that, copy from second to first. It turns out, just mixed.
All actions with an array of nine bytes are repeated for the second part of the password. We get two arrays:

Go to the function "moshnaja obrabotka kuchi":
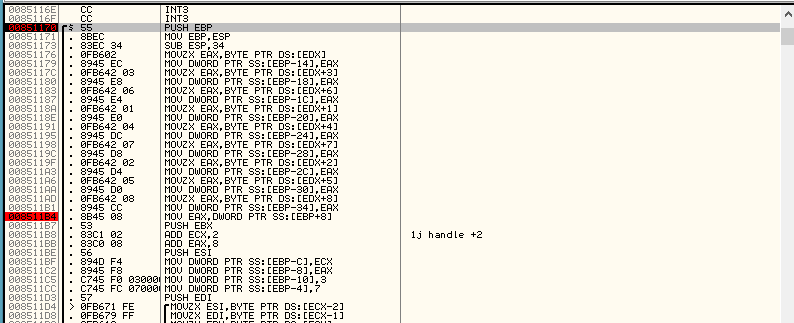
We see the transfer of the second array to the stack. We denote the array by B, and the beginning of the region to which we are transferred - D. On :
Next is a long cycle that runs 3 times:
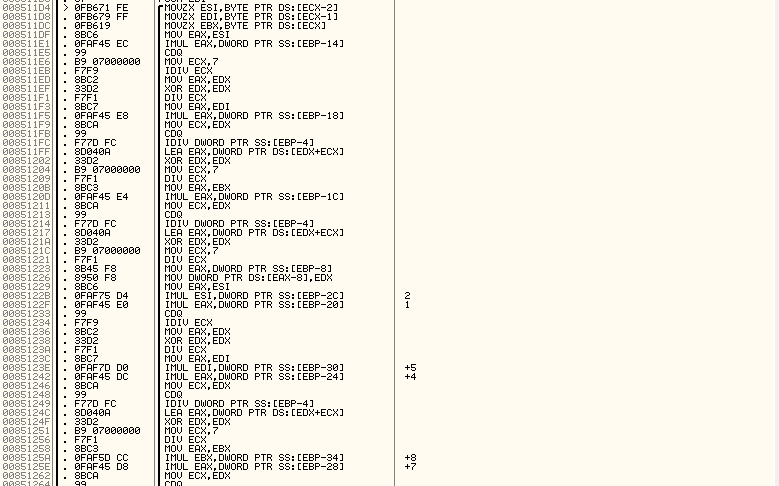

Not everyone will have enough patience, so just replace it with the algorithm in C. Let A be the first array, D the array in the stack, and E the new array for output, everything else is intermediate variables, and I am the decompiler. Then:
We leave the function, and the array of values in E is compared with the array [1,0,0,0,1,0,0,0,1]:
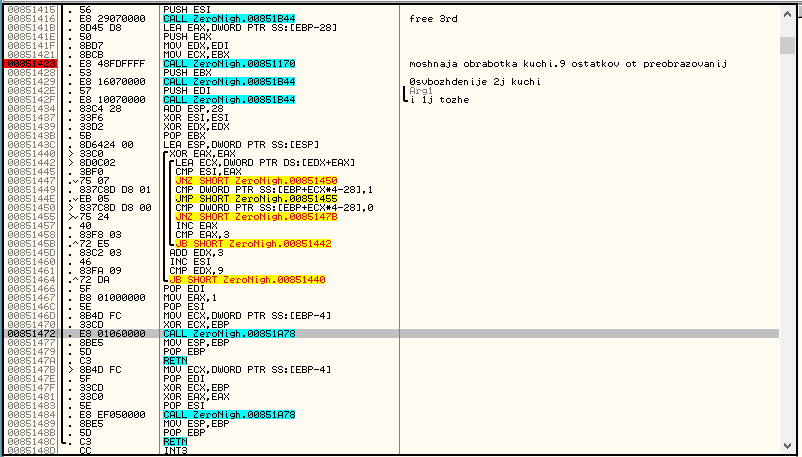
If matched, then the serial is correct.
So what is the matrix. First, any array of nine elements can be represented as a 3 by 3 matrix. We use this assumption. It turns out that the two parts of the password are two matrices. Remember that strange shuffle:
Each line of the matrix is shifted to its number.
Now let's take a closer look at transferring the second array to the stack:
And this is the interpolation of the matrix. Why do you need interpolation? Because a function that takes two arrays of nine bytes per input multiplies them as matrices. And where does% 7 come from? It's simple. The matrix cells use modular arithmetic in the field modulo 7.
Then the array [1,0,0,0,1,0,0,0,1] is also clear. In the matrix view, this is the identity matrix.
So, how do we find the key for our mail? I did not write Keigen, because there is no key for any mail, and now you will understand why.
After mixing the array by mail, we get 16 items that we can use. That is, we can put any of these elements in any cell of our two matrices. Since then only modular arithmetic will be used, it is possible to establish the equivalence of these elements to the members of the field modulo 7. From these elements we need to choose two opposite matrices so that when multiplied, we obtain the identity matrix. We try:
The main thing - do not forget about the offset to the line number.
As we select opposite matrices:
We find a symbol that turns into 0 and we find two symbols that turn into opposite elements (for example, 4 and 2).
If we have 1 - we are lucky.
The problem of Keygen is that we do not always have elements from which it is possible to make opposite matrices.
Any tips and comments are welcome. Thank you for reading to the end.
Enter random values. Get MessageBox with Fail:

Open the Modules window (large M) in an ollie. Press Ctrl + B (Search). Enter the value fail in the ASCII field. Hit on search - found:
')

Right-click on the first byte of the message, Breakpoit -> Memory -> On Access.
We start debugging. Enter the same values in the crackme fields. We get on passing the MessageBox parameters:

Before push with our line the conditional transition JNZ is visible. Before him TEST EAX, EAX. That is, if EAX is not zero, then MessageBox crashes with the string
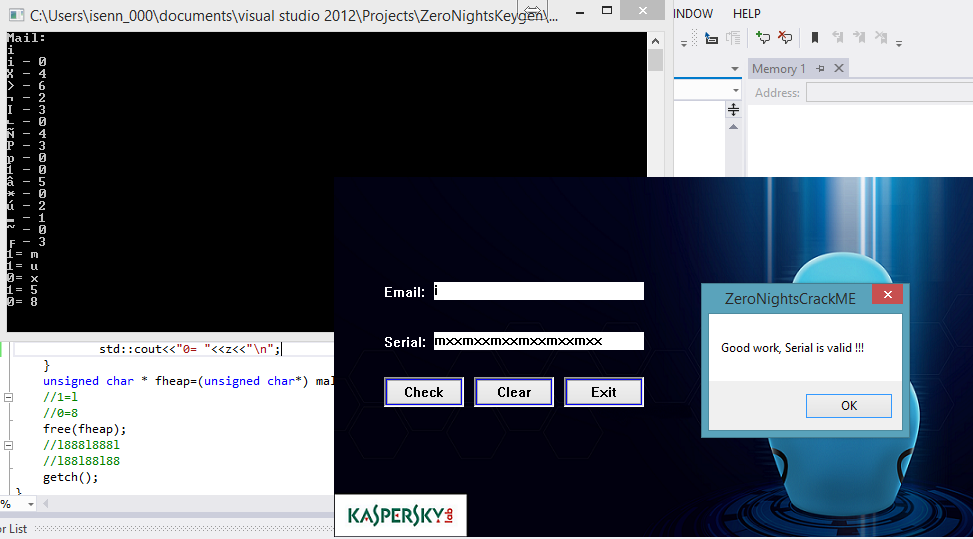
Good work, serial is valid!. We look, whence we receive EAX. Before comparison, there is a CALL. Apparently, in this function the key is checked. Let's see what's being passed on to her. Through the stack, the length of the password and the pointer to the mail line are transmitted. In the ECX register, a pointer is passed to the string with the password. Enter the function:

We look at the first JNZ. Before it, the password length is compared with 0x12 (18 in decimal). If not, Fail. Next is the cycle (it is highlighted with a black bracket on the left), in which the password character is checked. They must belong to the sets 0-9, AZ and az. From the comments on the right one can understand that not all functions are important for reverse. Some are simply functions of copying or highlighting arrays and are not of particular interest. The first function after the loop is very important, so we will consider it in detail:

Immediately noticeable two cycles. What happens in them? In the first, we fill the array in memory with values from 0 to 255.
In the second cycle, everything is not so simple. Two pointers are taken: on the array, filled in the first cycle, and on the line with the mail. An array element is taken by the cycle number and a character from the mail by the cycle number modulo the mail length. These bytes are summed modulo 256 (AND AND EDI operation, 0xFF is equivalent to __edi% 0x100 in syntax C). 2 item numbers are obtained in a loop step and received at the expense of mail. These 2 elements are swapped. Mail is the key with which the substitution of elements from 0 to 256 is performed. Simply the array is mixed. We leave from this function back to the general. Next, the array is allocated to 9 bytes and the first 9 characters of the password are copied into it. We will not consider these functions. Let's enter the function with a comment on translit starting with “hHeap zabivajetsa”:

It looks scary, but if you look closely, you can see that the actions are repeated, which means that we have a developed cycle. It is enough to consider only one iteration, everything else is identical.
The first character of the array of 9 bytes is placed in EDX. That is the first character of the password. Further magic:
MOV EAX, EDX
SHR EAX, 4
SHL EAX, 3
SUB EDX, EAX
AND EDX, 0F
In C, it will be:
EDX=(EDX- ((EDX >>4 )<<3))%16 Replace the password character in hHeap with the value from our mixed array using the EDX number. For the remaining characters is similar. Exit the function.
Another array is allocated for 9 bytes and the values from the first array are transferred to it, but according to certain rules:

Moving is a block of MOV and MOVZX. Let the first array A, and the second - B. On C:
b[0]=a[0]; b[1]=a[1]; b[2]=a[2]; b[3]=a[5]; b[4]=a[3]; b[5]=a[4]; b[6]=a[8]; b[7]=a[6]; b[8]=a[7]; After that, copy from second to first. It turns out, just mixed.
All actions with an array of nine bytes are repeated for the second part of the password. We get two arrays:

Go to the function "moshnaja obrabotka kuchi":

We see the transfer of the second array to the stack. We denote the array by B, and the beginning of the region to which we are transferred - D. On :
D[0]=B[0]; D[1]=B[3]; D[2]=B[6]; D[3]=B[1]; D[4]=B[4]; D[5]=B[7]; D[6]=B[2]; D[7]=B[5]; D[8]=B[8]; Next is a long cycle that runs 3 times:


Not everyone will have enough patience, so just replace it with the algorithm in C. Let A be the first array, D the array in the stack, and E the new array for output, everything else is intermediate variables, and I am the decompiler. Then:
for(int i=0;i<3;i++){ X[0]=A[0+i*3]; X[1]=A[1+i*3]; X[2]=A[2+i*3]; E[0+i*3]=((X[0]*D[0])%7+(X[1]*D[1])%7+(X[2]*D[2])%7)%7; E[1+i*3]=((X[0]*D[3])%7+(X[1]*D[4])%7+(X[2]*D[5])%7)%7; E[2+i*3]=((X[0]*D[6])%7+(X[1]*D[7])%7+(X[2]*D[8])%7)%7; } We leave the function, and the array of values in E is compared with the array [1,0,0,0,1,0,0,0,1]:

If matched, then the serial is correct.
So what is the matrix. First, any array of nine elements can be represented as a 3 by 3 matrix. We use this assumption. It turns out that the two parts of the password are two matrices. Remember that strange shuffle:
b[0]=a[0]; b[1]=a[1]; b[2]=a[2]; b[3]=a[5]; b[4]=a[3]; b[5]=a[4]; b[6]=a[8]; b[7]=a[6]; b[8]=a[7]; Each line of the matrix is shifted to its number.
Now let's take a closer look at transferring the second array to the stack:
D[0]=B[0]; D[1]=B[3]; D[2]=B[6]; D[3]=B[1]; D[4]=B[4]; D[5]=B[7]; D[6]=B[2]; D[7]=B[5]; D[8]=B[8]; And this is the interpolation of the matrix. Why do you need interpolation? Because a function that takes two arrays of nine bytes per input multiplies them as matrices. And where does% 7 come from? It's simple. The matrix cells use modular arithmetic in the field modulo 7.
Then the array [1,0,0,0,1,0,0,0,1] is also clear. In the matrix view, this is the identity matrix.
So, how do we find the key for our mail? I did not write Keigen, because there is no key for any mail, and now you will understand why.
After mixing the array by mail, we get 16 items that we can use. That is, we can put any of these elements in any cell of our two matrices. Since then only modular arithmetic will be used, it is possible to establish the equivalence of these elements to the members of the field modulo 7. From these elements we need to choose two opposite matrices so that when multiplied, we obtain the identity matrix. We try:

The main thing - do not forget about the offset to the line number.
As we select opposite matrices:
We find a symbol that turns into 0 and we find two symbols that turn into opposite elements (for example, 4 and 2).
If we have 1 - we are lucky.
The problem of Keygen is that we do not always have elements from which it is possible to make opposite matrices.
Any tips and comments are welcome. Thank you for reading to the end.
Source: https://habr.com/ru/post/204698/
All Articles