Everyone knows that the fastest method from the exchange sorting class is the so-called quick sorting . About her write a thesis, it is devoted to many articles on Habré, based on it come up with complex hybrid algorithms. But today we are not talking about quick sort , but about another exchange method - the good old bubble sort and its improvements, modifications, mutations and varieties.



Practical exhaust from these methods is not so hot, and many habrausers passed all this in the first grade. Therefore, the article is addressed to those who are just interested in the theory of algorithms and take the first steps in this direction.



image: bubbles

')





Today we will talk about the simplest sorting exchanges .



If anyone is interested, I will say that there are other classes - sorting by choice , sorting by inserts , merge sorting , distribution sorting , hybrid sorting and parallel sorting . There are, by the way, more esoteric sorting . These are various fake, basically unrealizable, comic, and other pseudo-algorithms, about which I will write a couple of articles in the IT-Humor hub sometime.



But this has nothing to do with today's lecture, we are now only interested in simple sorting exchanges. There are also quite a few sortings of exchanges (I know more than a dozen), so we will look at the so-called bubble sort and some others that are closely interrelated with it.



I will warn you in advance that almost all the above methods are very slow and there will not be a deep analysis of their time complexity. Some faster, some slower, but, roughly speaking, we can say that on average O ( n ² ). Also, I do not see any reason to clutter an article with implementations in any programming languages. Those who are interested can easily find code examples on Rosetta , on Wikipedia or anywhere else.



But back to the sorting exchanges. Ordering occurs as a result of multiple sequential brute force and comparison of pairs of elements among themselves. If the compared elements are not sorted relative to each other - then swap them. The only question is how exactly Makar array to bypass and on what principle to choose pairs for comparison.



Let's start not with the reference bubble sort, but with an algorithm called ...

Stupid sorting

Sorting really stupid. We look through the array from left to right and compare the neighbors along the way. If we meet a pair of mutually unsorted items, then we change them in places and return to their own place, that is, to the very beginning. Passing through the array again, if we meet again the “wrong” pair of neighboring elements, we switch places and start all over again. We continue until the array is slowly sortedly sorted.







“So any fool can sort” - you will say and you will be absolutely right. That is why sorting and nicknamed "stupid." In this lecture, we will consistently improve and modify this method. Now he has the time complexity O ( n ³ ), making one correction, we will bring it to O ( n ² ), then we will accelerate a little more, then another, and in the end we will get O ( n log n ) - and it will be Not "Quick Sort"!



Let's make a single improvement to the stupid sorting. Having found two neighboring unsorted elements during the passage and swapping them, we will not roll back to the beginning of the array, but calmly continue its detour to the very end.



In this case, we have nothing more than everyone knows ...

Bubble Sort

Or sorting by simple exchanges . Immortal classics of the genre. The procedure is simple: we go around the array from the beginning to the end, changing the unsorted adjacent elements along the way. As a result of the first pass, the maximum element “pops up” to the last place. Now we go around the unsorted part of the array (from the first element to the penultimate one) and change the unsorted neighbors along the way. The second largest element will be in the penultimate place. Continuing in the same vein, we will bypass the ever decreasing unsorted part of the array, stuffing the found maxima to the end.







If not only pushing highs at the end, but also throwing lows at the beginning, then we get ...

Shaker sorting

It is sorting by mixing , it is also cocktail sorting . The process begins as in a “bubble”: squeezing the maximum to the backyard. After that, we turn around to 180 ⁰ and go in the opposite direction, while already rolling at the beginning not the maximum, but the minimum. Sorting the first and the last elements in the array, again do somersault. After going round and round several times, we end up with the process, being in the middle of the list.







Shaker sorting is slightly faster than bubble sorting, since maxima and minima alternately migrate through the array in the right directions. Improvements, as they say, are obvious.



As you can see, if the brute force process is approached creatively, then pushing out heavy (light) elements to the ends of the array occurs faster. Therefore, the craftsmen offered to bypass the list another non-standard "road map".

Even-odd sort

This time we will not go back and forth through the array, but again we will return to the idea of ​​a systematic detour from left to right, but just take a wider step. On the first pass, elements with an odd key are compared with neighbors based on even places (1st is compared with 2nd, then 3rd with 4th, 5th with 6th and so on). Then, on the contrary, the “even in a row” elements are compared / changed to the “odd” ones. Then again “odd-odd”, then again “even-odd”. The process stops when, after a successive two passes through the array (“odd-even” and “even-odd”), not a single exchange occurred. So sorted.







In the usual “bubble” during each pass, we systematically squeeze the current maximum into the end of the array. If, however, to jump around on even and odd indices, then at once all more or less large elements of the array simultaneously for one run are pushed to the right by one position. So it turns out faster.



Let's sort out the last painting * for Sortuvannya Bulbachka ** - Sortuvane by combinants ***. This method organizes very quickly, O ( n ² ) - its worst complexity. On average, we have O ( n log n ) in time, and the best one even does not believe it, O ( n ). That is, a very worthy competitor to every sort of “quick sorting” and note this without using recursion. However, I promised that today we will not go into cruising speeds, we stop talking and turn directly to the algorithm.

Turtles are to blame

A little background. In 1980, Wlodzimierz Dobosiyevich explained why bubble sorts and derivatives derived from it work so slowly. This is all because of the turtles . “Turtles” are small items that are at the bottom of the list. As you may have noticed, bubble sorts are focused on “rabbits” (not to be confused with Babushkin's “rabbits”), which are large in value at the top of the list. They are very briskly moving to the finish line. But slow reptiles at the start crawling reluctantly. You can customize the "tortilla" using a comb .



image: guilty bug

Hairbrush sorting

In the "bubble", "shaker" and "even-odd" when searching an array, adjacent elements are compared. The basic idea of ​​combing is initially to take a sufficiently large distance between the compared elements and, as the array is ordered, to narrow this distance down to the minimum. Thus, we kind of comb the array, gradually smoothing it into neater strands.







The initial gap between the compared elements is better to take, not anyhow, but with the special value called the reduction factor , the optimal value of which is approximately 1.247. First, the distance between the elements is equal to the size of the array divided by the reduction factor (the result, of course, is rounded to the nearest integer). Then, having passed an array with this step, we again divide the step by the reduction factor and go through the list again. This continues until the index difference reaches unity. In this case, the array is sorted by the usual bubble.



Experimentally and theoretically, the optimal value of the reduction factor is established:







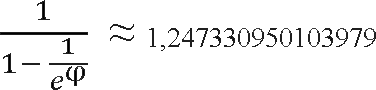
When this method was invented, very few people paid attention to it at the junction of the 70s and 80s. A decade later, when programming ceased to be the lot of IBM scientists and engineers, and already gained mass avalanche-like character, the method was rediscovered, researched and popularized in 1991 by Stephen Lacey and Richard Box.



That's all I wanted to tell you about bubble sorting and their ilk.



- Notes



* pokraschennya ( ukr. ) - improvement

** Sorbuvannya Bulbaska ( ukr. ) - Sort by bubble

*** Sorting comb ( ukr. ) - Sort by comb