Calculation of the position of celestial bodies in the sky. Part 1
Not so long ago, the topic of Mars was very actively discussed. At that time, I had a question from which, due to my naive curiosity, I could not get rid of: “Where is Mars at the moment, which side?” And adjacent to it: “Anyway, how to determine the position of the other planets?” . Obviously, the trajectories of the planets relative to the earth will be very tricky. Of course, you can use planetariums, for example, but as you already understood, this is not our way.
In this series of articles, I will try as simply as possible to talk about the complex. As a result, we will write a simple program that will tell you where to look for the planets of our solar system for any given point on the earth's surface at a given point in time. My goal is to convey to the reader the essence of what lies behind the Kepler model of the orbit, so I will not use any well-known facts except the laws of Newton and the law of universal perception.
')
I ask all curious under kat.
It should be noted that the further presentation implies that the reader is a little familiar with Newton's laws, basic information from geometry, vector algebra and differential calculus.
In reality, if we take into account the mutual influence of the planets, the shift of the center of gravity of the solar system relative to the center of gravity of the sun, etc. the motion of the planets will prove to be extremely complex and not amenable to rigorous analytical definition. It is worth noting that even the three-body motion problem cannot be solved analytically. Therefore, let us immediately stipulate in which models we will work. We will consider the Keplerian orbit model. There are many other models, but all of them are semi-analytical and as a result most of them come down to determining the parameters of the Kepler orbit at the time point of interest. In other words, the Kepler orbit is an approximation of the complex motion of the planet at a given point in time. Kepler parameters of the orbits of the planets can be viewed here nssdc.gsfc.nasa.gov/planetary/factsheet , there is also indicated the epoch (in other words, time) at the moment when these parameters of the Kepler orbit give the exact position of the celestial body. Typically, this reference time is the epoch J2000.0 (noon January 1, 2000). The calculation of the movement of bodies for a short period of time with the help of the Kepler model is fairly accurate. Accuracy is enough to not notice the error visually or in a small telescope. Of course, to calculate the flight path to another planet, more accurate models are needed.
So, in order. Let's start with the basic assumptions of this model. It is assumed that the mass of the Sun is much greater than the mass of all the planets combined, from which it can be concluded that the interaction between the planet and the planet is negligible compared to the interaction between the sun and the planet. Thus, the task set can be carried out to the problem of the interaction of two bodies (that is, we can consider the interaction of each planet with the sun separately). Moreover, we assume that the mass of the planet is much smaller than the mass of the Sun, then the interaction is one-way, i.e. the planet does not affect the movement of the sun. Thus, we can view the planet as a material point moving in a gravitational field, the center of which is fixed. Like that:
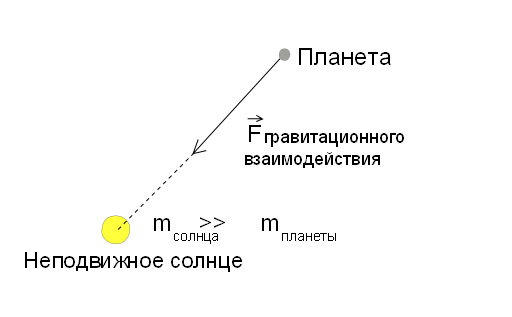
What is gravitational interaction? This is a universal fundamental interaction between all material bodies. About gravity can talk a lot and for a long time, but we need only a key point. According to the classical theory of Newton, the force of gravitational attraction between two material points of mass m 1 and m 2 , separated by distance R, is proportional to both masses and inversely proportional to the square of the distance between them - that is:
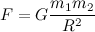
Here - G is the gravitational constant (a certain coefficient of proportionality). It is important for us to note only that the force of gravity is directed from the center of gravity of one body to the center of gravity of another and inversely proportional to the square of the distance between them (the law of inverse squares).
Note that the material point on ourspherical planet in vacuum is not affected by any other force, except for the force of attraction from the Sun. In our case, the field of forces is the central field of forces. In the central field of forces, the direction of the force acting on the body at any point of such a field always passes through the center of this field (in our case through the center of gravity of the sun), and the magnitude of such a force depends only on the distance to this center.
How does a body move by force? This question is answered by Newton's second law. In general, this law has several formulations, the most common of the modern:
This formulation is accurate, but not too clear. Newton himself gave a different wording:
This wording, though less accurate (you need to make reservations about the reporting system, but we are not interested in it yet), but much more understandable. The quantity of motion here means the so-called impulse of the body, equal to the product of the mass of the body and its speed:
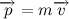
Thus, we write the verbal formulation in symbolic form:
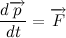
Or, if we write down what the body momentum is equal to and put the mass as a constant (mass is not always a constant, but in our case it is), we get the sign of the differential that we all know the following formula:
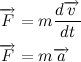
Where is the vector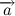 - acceleration of the body. Do not forget that the acceleration, momentum, speed and strength of the magnitude of the vector. Let's agree that if a vector sign stands above a vector quantity, then it is the vector that is understood, otherwise its module.
- acceleration of the body. Do not forget that the acceleration, momentum, speed and strength of the magnitude of the vector. Let's agree that if a vector sign stands above a vector quantity, then it is the vector that is understood, otherwise its module.
Let us, for simplicity, place the origin of the coordinates at the center of the center, i.e. in the center of gravity of the sun. Thus, the vector drawn from the center of gravity of the planet to the origin of coordinates coincides in direction with the vector of attractive force.
The position of the body in space is described by the so-called radius vector - a vector drawn from the origin to the center of gravity of the body. Multiply the vector left and right side of the expression by the radius vector:
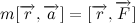
For further manipulations, let's write out the derivative of a vector product:
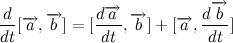
Then the derivative of the vector product of the velocity vector radius:
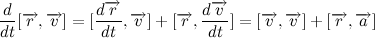
Let me remind you that the vector product of the vector itself is zero, then:
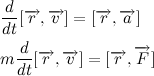
We introduce the mass under the sign of the differential, and taking into account the expression for the impulse of the body, we obtain:
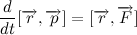
Since the vector of the force of attraction is always directed to the center of the vector, the vector product of the vector's radius and the force of attraction is always zero, hence we make a very important conclusion:
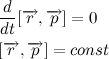
We obtained the so-called momentum conservation law. The change in the angular momentum of a body is proportional to the moment of force applied to it. Since the vector of the force of attraction is always directed to the center of the attraction, the moment of the force of attraction relative to the center of the attraction is always zero. It follows that the angular momentum of the body is constant.
Since we agreed that the mass of the planet is constant, the following expression is also true:
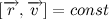
To understand what is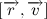 Let's turn to the picture:
Let's turn to the picture:

The figure shows the trajectory section. During dt, the body travels a distance vdt . The module of the vector product of vectors is numerically equal to the area of the parallelogram constructed on these vectors. Turns out that:
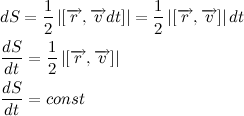
Magnitude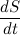 there is the area described by the radius vector per unit of time and is called sectorial velocity. Consequently, the sectorial velocity of the body is constant. We just got Kepler's second law, which says:
there is the area described by the radius vector per unit of time and is called sectorial velocity. Consequently, the sectorial velocity of the body is constant. We just got Kepler's second law, which says:
Yes, I know, “they got the law” does not sound good, but what can you do, that's what it is called. The reason is that Kepler did not deduce him, but intuitively picked up on the basis of his observations, i.e. got it empirically, in this case it really was the law.
Below is an illustration of this law (the picture is taken from an article on Wikipedia ).

Let's take a closer look at the vector product of the radius of the vector and speed. The radius of the vector can be represented as a product of the modulus of the radius of the vector (distance from the origin of coordinates to a point) by a vector of unit length that coincides in direction with the radius of the vector:
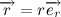

Then the velocity vector will be equal to:
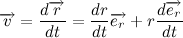
And the vector product of the vector radius and velocity in turn:
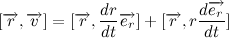
Given the fact that the vectors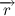 and
and 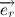 coincide in direction, and therefore coincide in direction and vector
coincide in direction, and therefore coincide in direction and vector 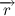 and
and  we get that
we get that  . Then:
. Then:

Let's analyze what the derivative of a unit vector is in time:
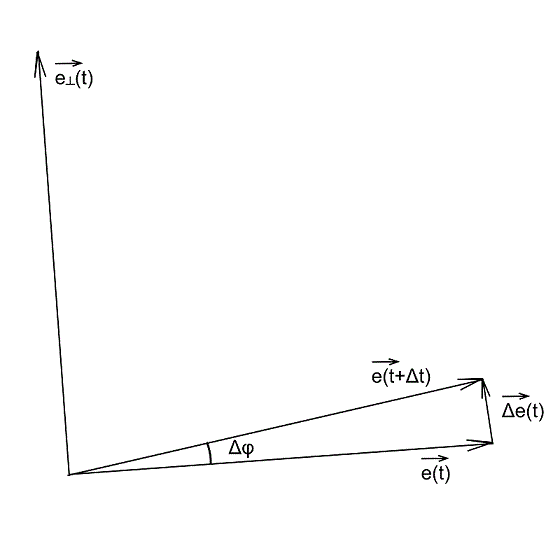
From the figure it is clear that in time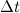 vector
vector 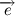 turns at an angle
turns at an angle 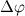 . Vector difference
. Vector difference 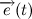 and
and  equal to vector
equal to vector 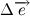 . For small angles, the following relationship holds true:
. For small angles, the following relationship holds true:

In the limit when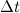 rushes to zero, vectors directions
rushes to zero, vectors directions 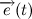 and
and  match, and the direction of the vector
match, and the direction of the vector 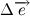 perpendicular to them. Introduce the unit vector
perpendicular to them. Introduce the unit vector 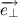 perpendicular to
perpendicular to 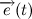 and coinciding with the direction of its end, then:
and coinciding with the direction of its end, then:
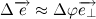
Thus, passing to the limit, we get:
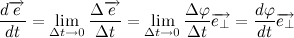
Where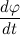 this is the angular velocity of the vector
this is the angular velocity of the vector 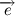 . Denote
. Denote 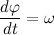
Let us return to our product, the radius of the velocity vector, given that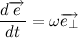 we will receive:
we will receive:
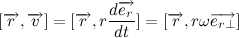
It is easy to see that the vector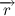 and
and 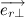 mutually perpendicular. We introduce another unit vector
mutually perpendicular. We introduce another unit vector 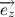 which is perpendicular to the vectors
which is perpendicular to the vectors 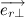 and
and 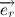 . So the vectors
. So the vectors 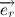 ,
, 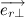 and
and 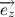 form an orthonormal basis. Based on the definition of a vector product, we get:
form an orthonormal basis. Based on the definition of a vector product, we get:
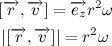
Consequently,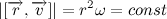 . We introduce the notation
. We introduce the notation 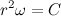 . It is also worth noting that:
. It is also worth noting that:

Let us return to the second law of Newton. Let us write out the force vector acting on the body immediately as the magnitude of the gravitational force multiplied by ort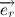 :
:
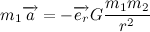
Where m 1 and m 2 are the mass of the planet and the sun, respectively.
Let's reduce the mass of the planet immediately, and nowhere else will we remember about the mass of the planet, because it does not affect the trajectory of motion at all. We assume that we work with the body of a unit mass. We introduce the notation , then:
, then:
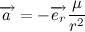
Now let's write the acceleration vector:
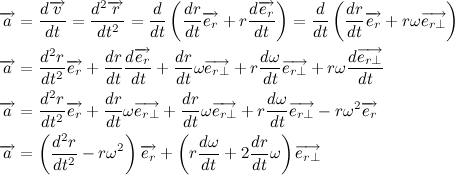
Consider the contents of the second bracket:
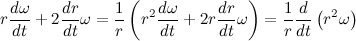
But we already know that it follows that
it follows that 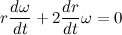 , then:
, then:
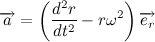
We introduce the notation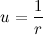 . Let me remind you that earlier we introduced the designation
. Let me remind you that earlier we introduced the designation 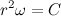 , it's obvious that
, it's obvious that 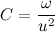 .
.
Now we shall write the derivative of the modulus of the radius of the vector through C:

Now we shall write the second derivative of the modulus of the radius of the vector through C:
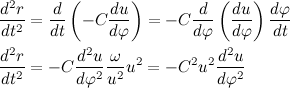
Given the result obtained, we rewrite the expression for the acceleration vector:
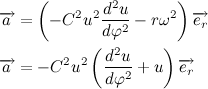
Then Newton's second law takes the form:
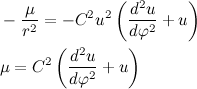
We rewrite the resulting differential equation in a more familiar form:
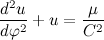
I think many of you have guessed what the resulting differential equation is, but I will probably finish the first part on this in order not to overload the reader and myself.
We have obtained a differential equation describing the trajectory of the motion of a material point in a gravitational field, which is quite applicable for describing the trajectory of the planets and some other celestial bodies.
In the resulting differential equation there is no time parameter, so we do not know anything about the nature of the movement, so it is necessary to somehow become attached to time. Also, different coordinate systems and their transformations will be considered in order to obtain the coordinates of the planets in the system attached to the observer.
Any criticism, comments and additions are welcome.
In this series of articles, I will try as simply as possible to talk about the complex. As a result, we will write a simple program that will tell you where to look for the planets of our solar system for any given point on the earth's surface at a given point in time. My goal is to convey to the reader the essence of what lies behind the Kepler model of the orbit, so I will not use any well-known facts except the laws of Newton and the law of universal perception.

')
I ask all curious under kat.
It should be noted that the further presentation implies that the reader is a little familiar with Newton's laws, basic information from geometry, vector algebra and differential calculus.
So how do the planets move?
In reality, if we take into account the mutual influence of the planets, the shift of the center of gravity of the solar system relative to the center of gravity of the sun, etc. the motion of the planets will prove to be extremely complex and not amenable to rigorous analytical definition. It is worth noting that even the three-body motion problem cannot be solved analytically. Therefore, let us immediately stipulate in which models we will work. We will consider the Keplerian orbit model. There are many other models, but all of them are semi-analytical and as a result most of them come down to determining the parameters of the Kepler orbit at the time point of interest. In other words, the Kepler orbit is an approximation of the complex motion of the planet at a given point in time. Kepler parameters of the orbits of the planets can be viewed here nssdc.gsfc.nasa.gov/planetary/factsheet , there is also indicated the epoch (in other words, time) at the moment when these parameters of the Kepler orbit give the exact position of the celestial body. Typically, this reference time is the epoch J2000.0 (noon January 1, 2000). The calculation of the movement of bodies for a short period of time with the help of the Kepler model is fairly accurate. Accuracy is enough to not notice the error visually or in a small telescope. Of course, to calculate the flight path to another planet, more accurate models are needed.
Kepler's orbit
So, in order. Let's start with the basic assumptions of this model. It is assumed that the mass of the Sun is much greater than the mass of all the planets combined, from which it can be concluded that the interaction between the planet and the planet is negligible compared to the interaction between the sun and the planet. Thus, the task set can be carried out to the problem of the interaction of two bodies (that is, we can consider the interaction of each planet with the sun separately). Moreover, we assume that the mass of the planet is much smaller than the mass of the Sun, then the interaction is one-way, i.e. the planet does not affect the movement of the sun. Thus, we can view the planet as a material point moving in a gravitational field, the center of which is fixed. Like that:

Gravitational interaction
What is gravitational interaction? This is a universal fundamental interaction between all material bodies. About gravity can talk a lot and for a long time, but we need only a key point. According to the classical theory of Newton, the force of gravitational attraction between two material points of mass m 1 and m 2 , separated by distance R, is proportional to both masses and inversely proportional to the square of the distance between them - that is:
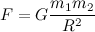
Here - G is the gravitational constant (a certain coefficient of proportionality). It is important for us to note only that the force of gravity is directed from the center of gravity of one body to the center of gravity of another and inversely proportional to the square of the distance between them (the law of inverse squares).
Note that the material point on our
Newton's Second Law
How does a body move by force? This question is answered by Newton's second law. In general, this law has several formulations, the most common of the modern:
In inertial reference systems, the acceleration acquired by a material point, in direct proportion to the force causing it, coincides with it in the direction and inversely proportional to the mass of the material point.
This formulation is accurate, but not too clear. Newton himself gave a different wording:
The change in the amount of motion is proportional to the applied driving force and occurs in the direction of the straight line along which this force acts.
This wording, though less accurate (you need to make reservations about the reporting system, but we are not interested in it yet), but much more understandable. The quantity of motion here means the so-called impulse of the body, equal to the product of the mass of the body and its speed:
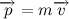
Thus, we write the verbal formulation in symbolic form:
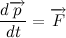
Or, if we write down what the body momentum is equal to and put the mass as a constant (mass is not always a constant, but in our case it is), we get the sign of the differential that we all know the following formula:
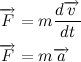
Where is the vector
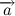 - acceleration of the body. Do not forget that the acceleration, momentum, speed and strength of the magnitude of the vector. Let's agree that if a vector sign stands above a vector quantity, then it is the vector that is understood, otherwise its module.
- acceleration of the body. Do not forget that the acceleration, momentum, speed and strength of the magnitude of the vector. Let's agree that if a vector sign stands above a vector quantity, then it is the vector that is understood, otherwise its module.Kepler's second law
Let us, for simplicity, place the origin of the coordinates at the center of the center, i.e. in the center of gravity of the sun. Thus, the vector drawn from the center of gravity of the planet to the origin of coordinates coincides in direction with the vector of attractive force.
The position of the body in space is described by the so-called radius vector - a vector drawn from the origin to the center of gravity of the body. Multiply the vector left and right side of the expression by the radius vector:
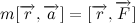
For further manipulations, let's write out the derivative of a vector product:
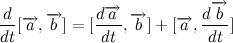
Then the derivative of the vector product of the velocity vector radius:
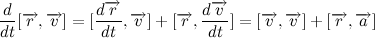
Let me remind you that the vector product of the vector itself is zero, then:
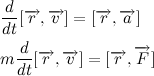
We introduce the mass under the sign of the differential, and taking into account the expression for the impulse of the body, we obtain:
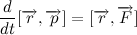
Since the vector of the force of attraction is always directed to the center of the vector, the vector product of the vector's radius and the force of attraction is always zero, hence we make a very important conclusion:
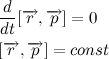
We obtained the so-called momentum conservation law. The change in the angular momentum of a body is proportional to the moment of force applied to it. Since the vector of the force of attraction is always directed to the center of the attraction, the moment of the force of attraction relative to the center of the attraction is always zero. It follows that the angular momentum of the body is constant.
Since we agreed that the mass of the planet is constant, the following expression is also true:
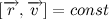
To understand what is
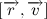 Let's turn to the picture:
Let's turn to the picture:
The figure shows the trajectory section. During dt, the body travels a distance vdt . The module of the vector product of vectors is numerically equal to the area of the parallelogram constructed on these vectors. Turns out that:
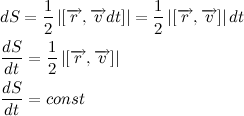
Magnitude
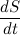 there is the area described by the radius vector per unit of time and is called sectorial velocity. Consequently, the sectorial velocity of the body is constant. We just got Kepler's second law, which says:
there is the area described by the radius vector per unit of time and is called sectorial velocity. Consequently, the sectorial velocity of the body is constant. We just got Kepler's second law, which says:Each planet moves in a plane passing through the center of the sun, and for equal periods of time the radius vector connecting the sun and the planet describes equal areas.
Yes, I know, “they got the law” does not sound good, but what can you do, that's what it is called. The reason is that Kepler did not deduce him, but intuitively picked up on the basis of his observations, i.e. got it empirically, in this case it really was the law.
Below is an illustration of this law (the picture is taken from an article on Wikipedia ).
Orbit Differential Equation
Let's take a closer look at the vector product of the radius of the vector and speed. The radius of the vector can be represented as a product of the modulus of the radius of the vector (distance from the origin of coordinates to a point) by a vector of unit length that coincides in direction with the radius of the vector:
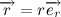

Then the velocity vector will be equal to:
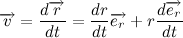
And the vector product of the vector radius and velocity in turn:
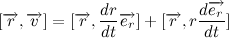
Given the fact that the vectors
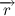 and
and 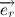 coincide in direction, and therefore coincide in direction and vector
coincide in direction, and therefore coincide in direction and vector 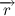 and
and  we get that
we get that  . Then:
. Then:
Let's analyze what the derivative of a unit vector is in time:
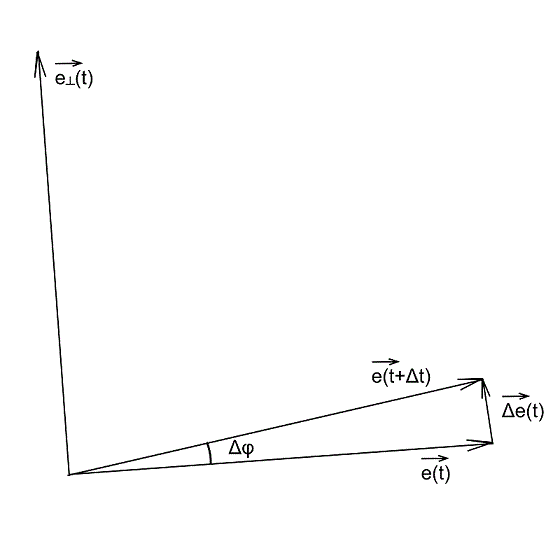
From the figure it is clear that in time
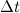 vector
vector 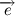 turns at an angle
turns at an angle 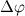 . Vector difference
. Vector difference 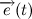 and
and  equal to vector
equal to vector 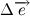 . For small angles, the following relationship holds true:
. For small angles, the following relationship holds true:
In the limit when
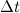 rushes to zero, vectors directions
rushes to zero, vectors directions 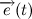 and
and  match, and the direction of the vector
match, and the direction of the vector 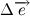 perpendicular to them. Introduce the unit vector
perpendicular to them. Introduce the unit vector 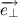 perpendicular to
perpendicular to 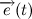 and coinciding with the direction of its end, then:
and coinciding with the direction of its end, then: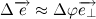
Thus, passing to the limit, we get:
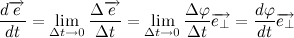
Where
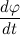 this is the angular velocity of the vector
this is the angular velocity of the vector 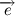 . Denote
. Denote 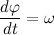
Let us return to our product, the radius of the velocity vector, given that
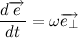 we will receive:
we will receive: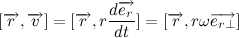
It is easy to see that the vector
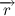 and
and 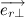 mutually perpendicular. We introduce another unit vector
mutually perpendicular. We introduce another unit vector 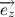 which is perpendicular to the vectors
which is perpendicular to the vectors 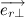 and
and 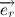 . So the vectors
. So the vectors 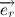 ,
, 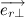 and
and 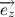 form an orthonormal basis. Based on the definition of a vector product, we get:
form an orthonormal basis. Based on the definition of a vector product, we get: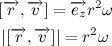
Consequently,
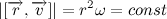 . We introduce the notation
. We introduce the notation 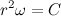 . It is also worth noting that:
. It is also worth noting that:
Let us return to the second law of Newton. Let us write out the force vector acting on the body immediately as the magnitude of the gravitational force multiplied by ort
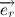 :
: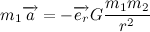
Where m 1 and m 2 are the mass of the planet and the sun, respectively.
Let's reduce the mass of the planet immediately, and nowhere else will we remember about the mass of the planet, because it does not affect the trajectory of motion at all. We assume that we work with the body of a unit mass. We introduce the notation
 , then:
, then: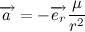
Now let's write the acceleration vector:
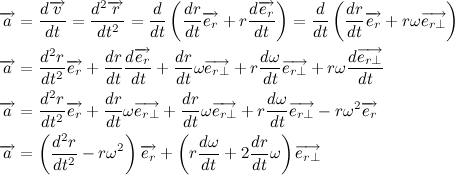
Consider the contents of the second bracket:
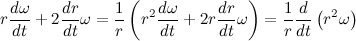
But we already know that
 it follows that
it follows that 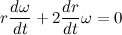 , then:
, then: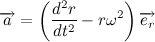
We introduce the notation
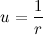 . Let me remind you that earlier we introduced the designation
. Let me remind you that earlier we introduced the designation 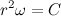 , it's obvious that
, it's obvious that 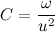 .
.Now we shall write the derivative of the modulus of the radius of the vector through C:

Now we shall write the second derivative of the modulus of the radius of the vector through C:
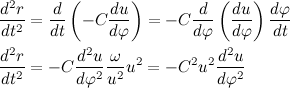
Given the result obtained, we rewrite the expression for the acceleration vector:
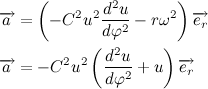
Then Newton's second law takes the form:
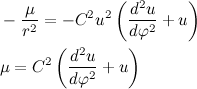
We rewrite the resulting differential equation in a more familiar form:
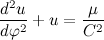
I think many of you have guessed what the resulting differential equation is, but I will probably finish the first part on this in order not to overload the reader and myself.
Total
We have obtained a differential equation describing the trajectory of the motion of a material point in a gravitational field, which is quite applicable for describing the trajectory of the planets and some other celestial bodies.
What we still have to
In the resulting differential equation there is no time parameter, so we do not know anything about the nature of the movement, so it is necessary to somehow become attached to time. Also, different coordinate systems and their transformations will be considered in order to obtain the coordinates of the planets in the system attached to the observer.
PS
Any criticism, comments and additions are welcome.
Source: https://habr.com/ru/post/204470/
All Articles