Finding periodic solutions of a class of non-autonomous systems of differential equations
In applied mathematics, sometimes there is the problem of constructing periodic solutions of the normal system of ordinary differential equations of the form
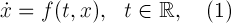
where is the function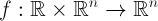 represents the sum
represents the sum
')
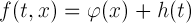
multidimensional polynomial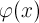 and trigonometric polynomial
and trigonometric polynomial 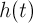 being
being 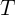 -periodic vector function.
-periodic vector function.
Many of the existence theorems for periodic solutions of system (1) use the fundamental fact that such solutions are completely determined by the fixed points of the shift operator along the trajectories of the system. However, the use of these theorems to directly find the desired periodic solution is most likely not possible.
Let it be known that system (1) has the only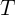 periodic solution
periodic solution 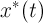 . Examples of systems that have a single periodic solution are systems with convergence (Pliss, VA, Nonlocal Problems of the Theory of Oscillations. - M., L .: Nauka, 1964). Consider one class of such systems for which you can build approximations to the solution
. Examples of systems that have a single periodic solution are systems with convergence (Pliss, VA, Nonlocal Problems of the Theory of Oscillations. - M., L .: Nauka, 1964). Consider one class of such systems for which you can build approximations to the solution 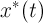 .
.
Let be - vector that
- vector that
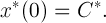
Here, for simplicity, we assume that the initial moment of time is zero. Then, if we can determine the vector then we will be able to construct the desired periodic solution.
then we will be able to construct the desired periodic solution.
We introduce the conditions imposed on the function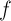 :
:
1. Let - a closed ball of radius r containing the solution values
- a closed ball of radius r containing the solution values 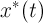 ,
,  - a closed ball of radius R , and
- a closed ball of radius R , and 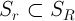 and there is such a positive number
and there is such a positive number 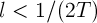 that for any
that for any 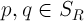 there is an inequality
there is an inequality

2. There is such a positive number.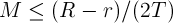 that for all
that for all 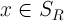 and any
and any 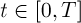 inequality holds
inequality holds
In fig. 1 shows a graphical illustration of these conditions for the system (1) of the second order.
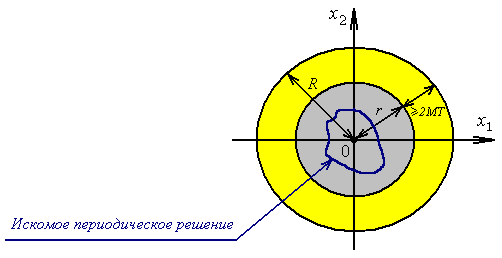
Fig. 1. Illustration of conditions 1-2 for the second order system.
In my work, it is shown that in this case successive approximations

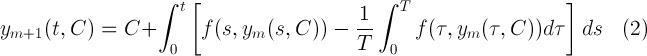
for any vector converge evenly for all
converge evenly for all 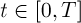 to some function
to some function 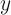 . And if you choose
. And if you choose  then it turns out that
then it turns out that
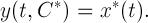
Based on formula (2), each iteration is calculated in symbolic form. Moreover, after transformations of trigonometric functions under the integral, one can always obtain a trigonometric polynomial with zero mean integral value. The analytical form of representing an approximation to a periodic solution is convenient in that it makes it possible to analyze the harmonics constituting this approximation. After calculating the next iteration, the function is built.
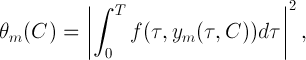
the minimum of which will give an approximation to the vector .
.
As an example, a second-order nonlinear system with convergence of the form (1) was considered (the values of the radii of the balls are indicated), where

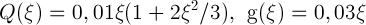 . It was found that at the first and second iterations the values of the found approximations to the vector
. It was found that at the first and second iterations the values of the found approximations to the vector  are the same and
are the same and
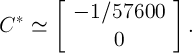
It has been verified that the trajectory of the second-order system under investigation, corresponding to the found initial point, returns to its vicinity after a period (Fig. 2).

Fig. 2. The arc of the trajectory corresponding to the found vector .
.
On this topic, you can see my report at the math conference (I apologize for the quality of the video - they filmed it on the phone).
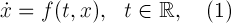
where is the function
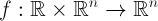 represents the sum
represents the sum')
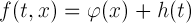
multidimensional polynomial
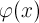 and trigonometric polynomial
and trigonometric polynomial 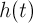 being
being 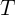 -periodic vector function.
-periodic vector function.Many of the existence theorems for periodic solutions of system (1) use the fundamental fact that such solutions are completely determined by the fixed points of the shift operator along the trajectories of the system. However, the use of these theorems to directly find the desired periodic solution is most likely not possible.
Let it be known that system (1) has the only
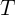 periodic solution
periodic solution 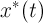 . Examples of systems that have a single periodic solution are systems with convergence (Pliss, VA, Nonlocal Problems of the Theory of Oscillations. - M., L .: Nauka, 1964). Consider one class of such systems for which you can build approximations to the solution
. Examples of systems that have a single periodic solution are systems with convergence (Pliss, VA, Nonlocal Problems of the Theory of Oscillations. - M., L .: Nauka, 1964). Consider one class of such systems for which you can build approximations to the solution 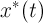 .
.Let be
 - vector that
- vector that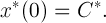
Here, for simplicity, we assume that the initial moment of time is zero. Then, if we can determine the vector
 then we will be able to construct the desired periodic solution.
then we will be able to construct the desired periodic solution.We introduce the conditions imposed on the function
 :
:1. Let
 - a closed ball of radius r containing the solution values
- a closed ball of radius r containing the solution values 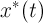 ,
,  - a closed ball of radius R , and
- a closed ball of radius R , and 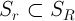 and there is such a positive number
and there is such a positive number 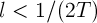 that for any
that for any 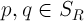 there is an inequality
there is an inequality
2. There is such a positive number.
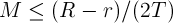 that for all
that for all 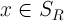 and any
and any 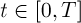 inequality holds
inequality holds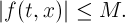
In fig. 1 shows a graphical illustration of these conditions for the system (1) of the second order.

Fig. 1. Illustration of conditions 1-2 for the second order system.
In my work, it is shown that in this case successive approximations

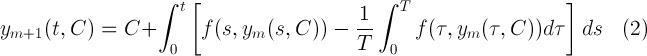
for any vector
 converge evenly for all
converge evenly for all 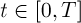 to some function
to some function 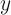 . And if you choose
. And if you choose  then it turns out that
then it turns out that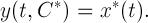
Based on formula (2), each iteration is calculated in symbolic form. Moreover, after transformations of trigonometric functions under the integral, one can always obtain a trigonometric polynomial with zero mean integral value. The analytical form of representing an approximation to a periodic solution is convenient in that it makes it possible to analyze the harmonics constituting this approximation. After calculating the next iteration, the function is built.
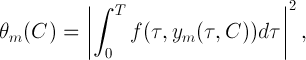
the minimum of which will give an approximation to the vector
 .
.As an example, a second-order nonlinear system with convergence of the form (1) was considered (the values of the radii of the balls are indicated), where

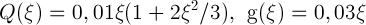 . It was found that at the first and second iterations the values of the found approximations to the vector
. It was found that at the first and second iterations the values of the found approximations to the vector  are the same and
are the same and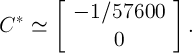
It has been verified that the trajectory of the second-order system under investigation, corresponding to the found initial point, returns to its vicinity after a period (Fig. 2).

Fig. 2. The arc of the trajectory corresponding to the found vector
 .
.On this topic, you can see my report at the math conference (I apologize for the quality of the video - they filmed it on the phone).
Source: https://habr.com/ru/post/204380/
All Articles