Generating functions back and forth
βThe generating function is a device, somewhat like a bag. Instead of carrying many items separately, which could be difficult, we put them together, and then we need to carry only one item - a bag. β
D. Poya
Mathematics is divided into two worlds - discrete and continuous. In the real world there is a place for both, and often one can approach the study of one phenomenon from different sides. In this article we will consider the method of solving problems using generating functions - the bridge leading from the discrete world to the continuous, and vice versa.
The idea of ββgenerating functions is quite simple: we associate a certain sequence <g 0 , g 1 , g 2 , ..., g n > to a discrete object, a power series g 0 + g 1 z + g 2 z 2 + ... + g n z n + ... - an object is continuous, thus we connect to the solution of the problem a whole arsenal of tools for mathematical analysis. It is usually said that the sequence is generated, generated by the generating function. It is important to understand that this is a symbolic construction, that is, instead of the z character there can be any object for which the operations of addition and multiplication are defined.
It is known that the English mathematician Abraham de Moivre initiated the method of generating functions, and we owe the further development and continuation of this method to the great mathematician whose name is Leonard Euler.
')
In the 50s of the 18th century, Euler solved the following problem: what loads can be weighed by 2,0,2,0,22,2 ..., 2n grams and in many ways? In solving this problem, he used an unknown at that time method of generating functions , which this article is devoted to. We will return to this task a little later, after we understand in more detail with the device of generating functions.
The study of this powerful mechanism allows us to solve many problems, we begin with a simple task: how many ways can black and white balls be arranged in a line, the total number of which is n?
Denote the white ball as β, black - β, T n is the required number of ball locations. The symbol Γ - denote the zero number of balls. As with any solution of the combinatorial problem, we start with the trivial cases:
If n = 1, then obviously there are 2 ways - to take either the white ball β or take the black ball β, thus, T 2 = 2.
If n = 2, then there are 4 ways of positioning: ββ, β β, β β, β β.
Consider the case for n = 3. We can start with a white ball and continue with 4 combinations described above βββ, ββ β, β β β, β ββ, or we can start with a black ball and similarly continue with 4 balls β ββ, β β β, ββ β, βββ.
As a result, the number of balls doubled, that is, T 3 = 2T 2 . Similarly, T 4 = 2T 3 , that is, generalizing for all n, we get the recurrent equation T n = 2T n-1 which is the solution for this problem. The solution of such an equation can be easily guessed - T n = 2 n (since 2β 2 n-1 = 2 n ).
And what if we have bad guessing? And what if the equation is more complicated? In general, where are the generating functions here?
Let's "sum up" all possible combinations of ball locations:
G = Γ + β + β + ββ + β β + β β + ββ + βββ + ββ β + β β β + β ββ + β ββ + β β β + ββ β + ββ β + ...
The question of the admissibility of such an absurd at first glance, the amount omitted. We will add and multiply the sequence of balls. With addition, everything is clear, but what does it mean to multiply one sequence of balls by another? Multiplying β β by β β we get nothing more than β ββ β. Note, however, that the product of balls, in contrast to the product of numbers, is not commutative, since β β β β β β β β β β. The Γ symbol - plays the role of a multiplicative unit in the product, that is, Γ β ββ β = ββ β β Γ = β β β and commutes with any sequence of balls.
Performing a sequence of manipulations with a number of G, namely by putting out the left white and black balls
G = Γ + β (Γ + β + β + ββ + β β + β β + ββ + ...) + β (Γ + β + β + ββ + β β + β β + ββ +. ..) = Γ + β G + β G
we obtain the equation G = Γ + β G + β G.
Despite the fact that multiplication is noncommutative, and we actually do not distinguish between left and right division, we will still try to βsolveβ this equation at our own risk. Will get
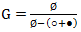
Given the formula for the sum of a geometric progression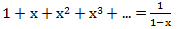
we have
.
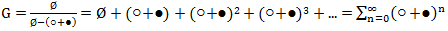This sum also takes into account all possible splitting options exactly once. Next, we use the Newton binomial formula:
where 
- the number of combinations of n for k. Then, with this in mind, we have:
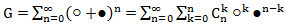
The coefficient for β k β nk equal to the number of combinations of n by k, shows the total number of sequences of n balls containing β balls in quantities of k pieces and β balls in the amount of nk pieces. Thus, the total number of arrangements of n balls is the sum over all possible values ββof k. As known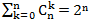
.
This formula could be obtained directly from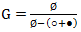 replacing Γ with 1, and β and β with z (in view of their equivalence). Will get 
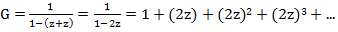that is, the coefficient at z n is 2 n .
So what allows this method to be workable in solving various problems?
The algorithm for solving the problem can be described approximately as follows: some infinite sum is considered, which ultimately represents a formal power series G (z) = g 0 + g 1 z + g 2 z 2 + ... + g n z n + ... and the coefficients g k (not specified explicitly) are the key to solving the original problem. The fact that the series is formal indicates that z is just a symbol, that is, instead of it there can be any object: a number, a ball, a domino bone, etc. In contrast to power series, in the analysis, formal power series are not given numerical values ββand, accordingly, there is no point in talking about the convergence of such series for numerical arguments.
G (z) = g 0 + g 1 z + g 2 z 2 +β¦ + g n z n +β¦ - is called the generating function for the sequence <g 0 , g 1 , g 2 , ..., g n >. Note, however, that although G (z) is a function, this is still a formal notation, that is, we cannot substitute any value z = z 0 for z, except for z = 0, since G (0) = g 0 .
Then, making various transformations with an infinite sum G (z), we transform it to a closed (compact) form. That is, the generating function has 2 representations: infinite and closed, and, as a rule, to solve the problem, it is necessary to convert the infinite form to a closed one, and then decompose the closed form into a power series, and thereby obtain values ββfor the coefficients g k .
Answering the question posed at the beginning, we can say this: the success of this method is connected with the ability to write the generating function in a closed form. So, for example, the generating function for the sequence <1, 1, 1, ..., 1> in the infinite form is represented as 1 + x + x 2 + x 3 + ..., and in the closed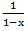
.
And now, having armed ourselves with knowledge, let us return to the problem that Euler solved.
So, the task is as follows: what loads can be weighed using 2 0 , 2 1 , 2 2 , ..., 2 n grams and how many ways?
I do not know how long Euler thought of a solution for this problem, but it is striking in its surprise. Judge for yourself. Euler considers the product G (z) = (1 + z) (1 + z 2 ) (1 + z 4 ) ... which, after opening the brackets, is represented as an infinite series G (z) = 1 + g 1 z + g 2 z 2 + g 3 z 3 + ....
What are the coefficients of g k ? Each g k is a coefficient at z k , and z k is obtained as the product of some monomials z 2m , that is, g k is exactly the number of different representations of the number k as the sum of some of the numbers 1, 2, 2 2 , 2 3 , ..., 2 m , .... In other words, g k is the number of ways to weigh a load in k grams by given weights. Just what we were looking for!
Euler's next step is striking no less than the previous one. It multiplies both sides of the equation by (1-z).
(1-z) G (z) = (1-z) (1 + z) (1 + z 2 ) (1 + z 4 ) (1 + z 8 ) ...
(1-z) G (z) = (1-z2) (1 + z 2 ) (1 + z 4 ) (1 + z 8 ) ...
(1-z) G (z) = (1-z 4 ) (1 + z 4 ) (1 + z 8 ) ...
(1-z) G (z) = 1
On the one hand, G (z) = 1 + g 1 z + g 2 z 2 + g 3 z 3 + ... on the other hand, we just got . The last equality is nothing but the sum of a geometric progression, which is equal to 
. Comparing these two equalities, we get g 1 = g 2 = g 3 = ... = 1, that is, any weight in k grams can be weighed in weights in 1, 2, 4, 8, ... grams, moreover, in the only way.
The generating functions are suitable for solving not only combinatorial problems. It turns out that they can be used to solve recurrent relations.
Let's start with all the familiar sequence of Fibonacci numbers. Each of us knows its recurrent form: F 0 = 0, F 1 = 1, F n = F n-1 + F n-2 , n β₯ 2. However, not everyone knows the form of this formula in a closed form and this is not surprising because it contains an irrational number ("golden section") in its composition.
So, we have
F 0 = 0,
F 1 = 1,
F n = F n-1 + F n-2 , n β₯ 2
Multiply each line by z 0 , z 1 , ..., z n, respectively:
z 0 β F 0 = 0,
z 1 β F 1 = z,
z n β F n = z n β F n-1 + z n β F n-2 , n β₯ 2
Sum up these equalities:
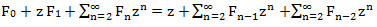
Denote the left side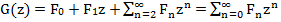
Consider each of the addends on the right side:
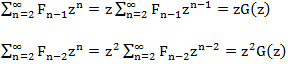
We have the following equation G (z) = z + z G (z) + z 2 G (z) solving which, with respect to G (z), we find
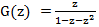- generating function for the sequence of Fibonacci numbers.
We decompose it into the sum of the simplest fractions, for this we find the roots of the equation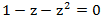
. Solving this simple quadratic equation, we get: 
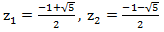. Then our generating function can be decomposed as follows:
The next step is to find the coefficients a and b. To do this, multiply the fraction by a common denominator:
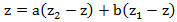
Substituting the value z = z 1 and z = z 2 into this equation, we find
Finally, we slightly transform the expression for the generating function.
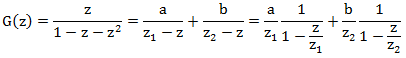
Now each of the fractions is the sum of a geometric progression.
According to the formula
we find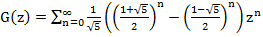 
But we were looking for G (z) in the form
. From here we conclude that
This formula can be rewritten in another form without using the "golden section":
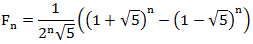
which was hard enough to expect, given the beautiful recurrence equation.
Let's write a general algorithm for solving recurrent equations using generating functions. It is written in 4 steps:
The reason why this method works is that the single function G (z) represents the entire sequence g n and this representation allows for many transformations.
Before proceeding to the next example, consider 2 operations performed on generating functions, which are often useful.
For generating functions, the usual definition of a derivative can be written as follows.
Let G = G (z) be a generating function. The derivative of this function is called the function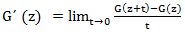
. Differentiation is obviously a linear operation; therefore, in order to understand how it acts on generating functions, it suffices to look at its action, on the powers of the variable. We have
Thus, the action of differentiation on an arbitrary generating function
G (z) = g 0 + g 1 z + g 2 z 2 + g 3 z 3 + ... gives GΞ (z) = g 1 + 2g 2 z + 3g 3 z 2 + 4g 4 z 3 + ....
The integral is called the function.
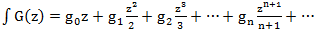
The operation of differentiation is inverse to the operation of integration:
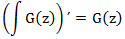
The operation of integrating the derivative leads to a function with a zero free term, and therefore the result is different from the original function,
It is easy to see that for functions that can be represented as power series, the formula for the derivative corresponds to the usual one. The formula for the integral corresponds to the value of the integral with a variable upper limit.
Using the knowledge we have just received about differentiating and integrating the generating functions, let us try to solve the following recurrence equation:
g 0 = 1,
g 1 = 1,
g n = g n-1 + 2g n-2 + (-1) n
We will follow the above algorithm. The first condition of the algorithm is satisfied. Multiply both sides of all equalities by z to the appropriate degree and sum up:
z 0 β g 0 = 1,
z 1 β g 1 = z,
z n β g n = z n β g n-1 + 2z n β g n-2 + (-1) n β z n
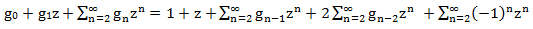
Left side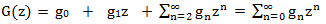
is a generating function in an infinite form.
Let us try to express the right-hand side in terms of G (z). Consider each term:
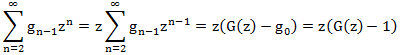
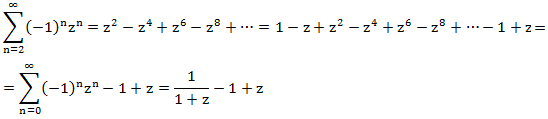
We make the equation:
This is the generating function for a given recurrence equation. Decomposing it into simple fractions (for example, by the method of undetermined coefficients or by substituting various values ββof z), we get:
The second and third terms are easily decomposed into a power series, but the first will have to be a little tricky. Using the rule of differentiation of generating functions we have:
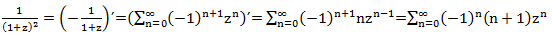
Actually everything. We decompose each term in a power series and get the answer:
On the one hand, we looked for G (z) in the form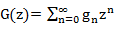
, on the other hand 
.
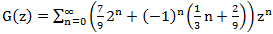So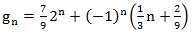
.
The generating functions have found great use in mathematics, since they are powerful weapons in solving many practical problems associated, for example, with the enumeration, distribution, and partitioning of sets of objects of different nature. In addition, the use of generating functions allows us to prove some combinatorial formulas that are otherwise very difficult to obtain. For example, the decomposition function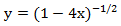
in power series has the form 
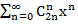, that is, the equality is true:
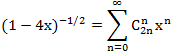
By squaring both sides of this equation we get
Equating the coefficients at x n in the left and right parts, we get
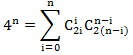
This formula has a clear combinatorial meaning, but it is not easy to prove it. Back in the 80s of the 20th century, publications appeared on this issue.
D. Poya
Introduction
Mathematics is divided into two worlds - discrete and continuous. In the real world there is a place for both, and often one can approach the study of one phenomenon from different sides. In this article we will consider the method of solving problems using generating functions - the bridge leading from the discrete world to the continuous, and vice versa.
The idea of ββgenerating functions is quite simple: we associate a certain sequence <g 0 , g 1 , g 2 , ..., g n > to a discrete object, a power series g 0 + g 1 z + g 2 z 2 + ... + g n z n + ... - an object is continuous, thus we connect to the solution of the problem a whole arsenal of tools for mathematical analysis. It is usually said that the sequence is generated, generated by the generating function. It is important to understand that this is a symbolic construction, that is, instead of the z character there can be any object for which the operations of addition and multiplication are defined.
History of generating functions
It is known that the English mathematician Abraham de Moivre initiated the method of generating functions, and we owe the further development and continuation of this method to the great mathematician whose name is Leonard Euler.
')
In the 50s of the 18th century, Euler solved the following problem: what loads can be weighed by 2,0,2,0,22,2 ..., 2n grams and in many ways? In solving this problem, he used an unknown at that time method of generating functions , which this article is devoted to. We will return to this task a little later, after we understand in more detail with the device of generating functions.
Method of generating functions
The study of this powerful mechanism allows us to solve many problems, we begin with a simple task: how many ways can black and white balls be arranged in a line, the total number of which is n?
Denote the white ball as β, black - β, T n is the required number of ball locations. The symbol Γ - denote the zero number of balls. As with any solution of the combinatorial problem, we start with the trivial cases:
If n = 1, then obviously there are 2 ways - to take either the white ball β or take the black ball β, thus, T 2 = 2.
If n = 2, then there are 4 ways of positioning: ββ, β β, β β, β β.
Consider the case for n = 3. We can start with a white ball and continue with 4 combinations described above βββ, ββ β, β β β, β ββ, or we can start with a black ball and similarly continue with 4 balls β ββ, β β β, ββ β, βββ.
As a result, the number of balls doubled, that is, T 3 = 2T 2 . Similarly, T 4 = 2T 3 , that is, generalizing for all n, we get the recurrent equation T n = 2T n-1 which is the solution for this problem. The solution of such an equation can be easily guessed - T n = 2 n (since 2β 2 n-1 = 2 n ).
And what if we have bad guessing? And what if the equation is more complicated? In general, where are the generating functions here?
Let's "sum up" all possible combinations of ball locations:
G = Γ + β + β + ββ + β β + β β + ββ + βββ + ββ β + β β β + β ββ + β ββ + β β β + ββ β + ββ β + ...
The question of the admissibility of such an absurd at first glance, the amount omitted. We will add and multiply the sequence of balls. With addition, everything is clear, but what does it mean to multiply one sequence of balls by another? Multiplying β β by β β we get nothing more than β ββ β. Note, however, that the product of balls, in contrast to the product of numbers, is not commutative, since β β β β β β β β β β. The Γ symbol - plays the role of a multiplicative unit in the product, that is, Γ β ββ β = ββ β β Γ = β β β and commutes with any sequence of balls.
Performing a sequence of manipulations with a number of G, namely by putting out the left white and black balls
G = Γ + β (Γ + β + β + ββ + β β + β β + ββ + ...) + β (Γ + β + β + ββ + β β + β β + ββ +. ..) = Γ + β G + β G
we obtain the equation G = Γ + β G + β G.
Despite the fact that multiplication is noncommutative, and we actually do not distinguish between left and right division, we will still try to βsolveβ this equation at our own risk. Will get
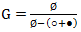
Given the formula for the sum of a geometric progression
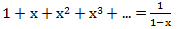we have 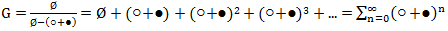.This sum also takes into account all possible splitting options exactly once. Next, we use the Newton binomial formula:
where - the number of combinations of n for k. Then, with this in mind, we have: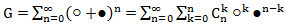The coefficient for β k β nk equal to the number of combinations of n by k, shows the total number of sequences of n balls containing β balls in quantities of k pieces and β balls in the amount of nk pieces. Thus, the total number of arrangements of n balls is the sum over all possible values ββof k. As known
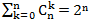.This formula could be obtained directly from
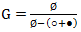replacing Γ with 1, and β and β with z (in view of their equivalence). Will get 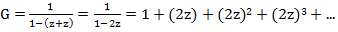that is, the coefficient at z n is 2 n .Method discussion
So what allows this method to be workable in solving various problems?
The algorithm for solving the problem can be described approximately as follows: some infinite sum is considered, which ultimately represents a formal power series G (z) = g 0 + g 1 z + g 2 z 2 + ... + g n z n + ... and the coefficients g k (not specified explicitly) are the key to solving the original problem. The fact that the series is formal indicates that z is just a symbol, that is, instead of it there can be any object: a number, a ball, a domino bone, etc. In contrast to power series, in the analysis, formal power series are not given numerical values ββand, accordingly, there is no point in talking about the convergence of such series for numerical arguments.
G (z) = g 0 + g 1 z + g 2 z 2 +β¦ + g n z n +β¦ - is called the generating function for the sequence <g 0 , g 1 , g 2 , ..., g n >. Note, however, that although G (z) is a function, this is still a formal notation, that is, we cannot substitute any value z = z 0 for z, except for z = 0, since G (0) = g 0 .
Then, making various transformations with an infinite sum G (z), we transform it to a closed (compact) form. That is, the generating function has 2 representations: infinite and closed, and, as a rule, to solve the problem, it is necessary to convert the infinite form to a closed one, and then decompose the closed form into a power series, and thereby obtain values ββfor the coefficients g k .
Answering the question posed at the beginning, we can say this: the success of this method is connected with the ability to write the generating function in a closed form. So, for example, the generating function for the sequence <1, 1, 1, ..., 1> in the infinite form is represented as 1 + x + x 2 + x 3 + ..., and in the closed
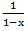.And now, having armed ourselves with knowledge, let us return to the problem that Euler solved.
So, the task is as follows: what loads can be weighed using 2 0 , 2 1 , 2 2 , ..., 2 n grams and how many ways?
I do not know how long Euler thought of a solution for this problem, but it is striking in its surprise. Judge for yourself. Euler considers the product G (z) = (1 + z) (1 + z 2 ) (1 + z 4 ) ... which, after opening the brackets, is represented as an infinite series G (z) = 1 + g 1 z + g 2 z 2 + g 3 z 3 + ....
What are the coefficients of g k ? Each g k is a coefficient at z k , and z k is obtained as the product of some monomials z 2m , that is, g k is exactly the number of different representations of the number k as the sum of some of the numbers 1, 2, 2 2 , 2 3 , ..., 2 m , .... In other words, g k is the number of ways to weigh a load in k grams by given weights. Just what we were looking for!
Euler's next step is striking no less than the previous one. It multiplies both sides of the equation by (1-z).
(1-z) G (z) = (1-z) (1 + z) (1 + z 2 ) (1 + z 4 ) (1 + z 8 ) ...
(1-z) G (z) = (1-z2) (1 + z 2 ) (1 + z 4 ) (1 + z 8 ) ...
(1-z) G (z) = (1-z 4 ) (1 + z 4 ) (1 + z 8 ) ...
(1-z) G (z) = 1
On the one hand, G (z) = 1 + g 1 z + g 2 z 2 + g 3 z 3 + ... on the other hand, we just got
. The last equality is nothing but the sum of a geometric progression, which is equal to . Comparing these two equalities, we get g 1 = g 2 = g 3 = ... = 1, that is, any weight in k grams can be weighed in weights in 1, 2, 4, 8, ... grams, moreover, in the only way.Recursion Solution
The generating functions are suitable for solving not only combinatorial problems. It turns out that they can be used to solve recurrent relations.
Let's start with all the familiar sequence of Fibonacci numbers. Each of us knows its recurrent form: F 0 = 0, F 1 = 1, F n = F n-1 + F n-2 , n β₯ 2. However, not everyone knows the form of this formula in a closed form and this is not surprising because it contains an irrational number ("golden section") in its composition.
So, we have
F 0 = 0,
F 1 = 1,
F n = F n-1 + F n-2 , n β₯ 2
Multiply each line by z 0 , z 1 , ..., z n, respectively:
z 0 β F 0 = 0,
z 1 β F 1 = z,
z n β F n = z n β F n-1 + z n β F n-2 , n β₯ 2
Sum up these equalities:
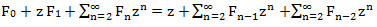
Denote the left side
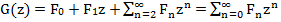
Consider each of the addends on the right side:
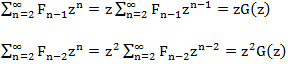
We have the following equation G (z) = z + z G (z) + z 2 G (z) solving which, with respect to G (z), we find
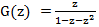- generating function for the sequence of Fibonacci numbers.We decompose it into the sum of the simplest fractions, for this we find the roots of the equation
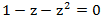. Solving this simple quadratic equation, we get: 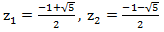. Then our generating function can be decomposed as follows:The next step is to find the coefficients a and b. To do this, multiply the fraction by a common denominator:
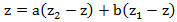
Substituting the value z = z 1 and z = z 2 into this equation, we find
Finally, we slightly transform the expression for the generating function.
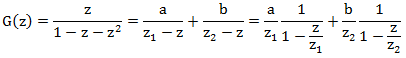
Now each of the fractions is the sum of a geometric progression.
According to the formula
we find 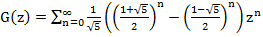But we were looking for G (z) in the form
. From here we conclude thatThis formula can be rewritten in another form without using the "golden section":
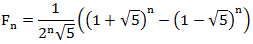
which was hard enough to expect, given the beautiful recurrence equation.
Let's write a general algorithm for solving recurrent equations using generating functions. It is written in 4 steps:
- Write one equation expressing gn through other elements of the sequence. This equation should remain valid for all integers n, taking into account the fact that g -1 = g -2 = ... = 0.
- Multiply both sides of the equation by z n and sum over all n. In the left part we get the amount
which is equal to the generating function G (z). The right side should be transformed so that it turns into some other expression, including G (z). - Solve the resulting equation by obtaining the closed-form expression for G (z).
- Lay out G (z) in a power series and read the coefficient at z n , this will be a closed form for g n .
The reason why this method works is that the single function G (z) represents the entire sequence g n and this representation allows for many transformations.
Before proceeding to the next example, consider 2 operations performed on generating functions, which are often useful.
Differentiation and integration of generating functions
For generating functions, the usual definition of a derivative can be written as follows.
Let G = G (z) be a generating function. The derivative of this function is called the function
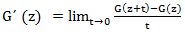. Differentiation is obviously a linear operation; therefore, in order to understand how it acts on generating functions, it suffices to look at its action, on the powers of the variable. We haveThus, the action of differentiation on an arbitrary generating function
G (z) = g 0 + g 1 z + g 2 z 2 + g 3 z 3 + ... gives GΞ (z) = g 1 + 2g 2 z + 3g 3 z 2 + 4g 4 z 3 + ....
The integral is called the function.
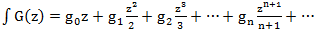
The operation of differentiation is inverse to the operation of integration:
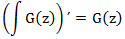
The operation of integrating the derivative leads to a function with a zero free term, and therefore the result is different from the original function,
It is easy to see that for functions that can be represented as power series, the formula for the derivative corresponds to the usual one. The formula for the integral corresponds to the value of the integral with a variable upper limit.
Using the knowledge we have just received about differentiating and integrating the generating functions, let us try to solve the following recurrence equation:
g 0 = 1,
g 1 = 1,
g n = g n-1 + 2g n-2 + (-1) n
We will follow the above algorithm. The first condition of the algorithm is satisfied. Multiply both sides of all equalities by z to the appropriate degree and sum up:
z 0 β g 0 = 1,
z 1 β g 1 = z,
z n β g n = z n β g n-1 + 2z n β g n-2 + (-1) n β z n
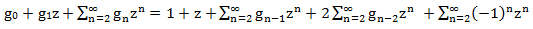
Left side
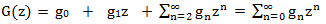is a generating function in an infinite form.Let us try to express the right-hand side in terms of G (z). Consider each term:
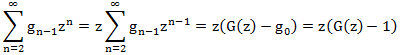
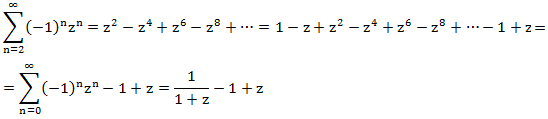
We make the equation:
This is the generating function for a given recurrence equation. Decomposing it into simple fractions (for example, by the method of undetermined coefficients or by substituting various values ββof z), we get:
The second and third terms are easily decomposed into a power series, but the first will have to be a little tricky. Using the rule of differentiation of generating functions we have:
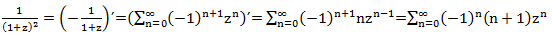
Actually everything. We decompose each term in a power series and get the answer:
On the one hand, we looked for G (z) in the form
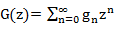, on the other hand 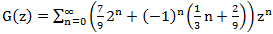.So
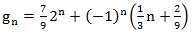.Instead of conclusion
The generating functions have found great use in mathematics, since they are powerful weapons in solving many practical problems associated, for example, with the enumeration, distribution, and partitioning of sets of objects of different nature. In addition, the use of generating functions allows us to prove some combinatorial formulas that are otherwise very difficult to obtain. For example, the decomposition function
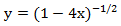in power series has the form 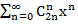, that is, the equality is true: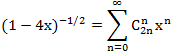By squaring both sides of this equation we get
Equating the coefficients at x n in the left and right parts, we get
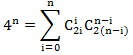
This formula has a clear combinatorial meaning, but it is not easy to prove it. Back in the 80s of the 20th century, publications appeared on this issue.
Source: https://habr.com/ru/post/204258/
All Articles