Optimization of enumeration of surfaces composed of triangles

There was a task to sort through all possible variants of "triangulations". These are “glues” of N triangles, which obey simple rules:

1. Triangles can touch only along the edge.
2. One edge can be common only for two triangles, not more

For example, out of three triangles of unique options there can be only two:
[[ABC], [ABD], [ACD]]
[[ABC], [ABD], [ACE]]

Despite the fact that there are 120 total gluing options. I managed to optimize the brute force process well, which made it possible to calculate almost all variants up to N = 11, but this is still very small.
I will tell you how optimized it may be for a respected public to have ideas on how to accelerate this process.

Naive approach

')
Consider a variant with N = 3. Three triangles, 9 vertices. We number the vertices 0 ... 8 and iterate over everything from 000 000 000 to 888 888 888.
As you can see, this is very dofiga even for three triangles. Well, the repeats of the triangles, which will constantly come across here, we do not need anything here.

Combinatorial approach

Long evenings of thought allowed the head to give birth to the following thought:
Since all triangles must be glued together with at least one edge, then the maximum number of vertices that will be needed for gluing N triangles must be less than N * 3

Indeed, the longest valid gluing will look like this:



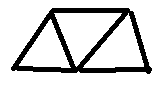
And it is clear that there are only 5 unique vertices instead of 9. In the general case, the number of unique vertices is obtained by the formula N + 2 , where N is the number of triangles. If there are more unique vertices, then one of the triangles will necessarily be connected to the other with only one vertex, and this is wrong.

So. 5 unique vertices for three triangles.
There will be a total of combinations (remember combinatorics and the binomial coefficient) 5! / (3! (5 - 3)!) = 10
This is the number of unique triangles that we can get by generating all the vertex combinations.

Now, consider the same binomial coefficient for combinations of three triangles.
ten! / (3! (10 - 3)!) = 120 . This is how many glues you need to sort out to take into account all the options.

In general, the formula for the number of combinations is as follows:



See how many factorials? For example, for N = 10, there will be 59,473,554,359,599,446 combinations in total, which is a lot, even if paralleled.

When I started busting with small N (3,4,5 ..) I noticed that the program quickly finds all the combinations, and the rest is just duplicates (they are eliminated by the VF2 algorithm, which checks the graphs for isomorphism)

Pretty quickly - this means that the last “good” gluing together for, for example, N = 5 was found at step 2084 from 324,632, which is 0.642% of the entire range. For N = 6, this is 0.3644%. The last thing I managed to calculate for myself - for N = 8, this is 0.1352%.

That is, in the general case for N + 1, we look at how many percent of the previous range were calculated and we count the same, this will guarantee us that everything is checked. The truth for N = 9 is still a bit too much (270 485 377 680, if you check 0.1352%)

So, it was necessary to invent something else.

Iterative approach

A few more long evenings and another idea:
And what if you generate all the glues for N + 1 based on all the glues for N by adding one triangle with all possible combinations?

That is, we know that for threes we have only two

[[ABC], [ABD], [ACD]]
[[ABC], [ABD], [ACE]]

And fours six

[[ABC], [ABD], [ACD], [BCD]]
[[ABC], [ABD], [ACD], [BCE]]
[[ABC], [ABD], [ACE], [ADE]]
[[ABC], [ABD], [ACE], [ADF]]
[[ABC], [ABD], [ACE], [BCF]]
[[ABC], [ABD], [ACE], [BDF]]

It can be seen that all the fours turned out from the previous triples (permutations are generated in lexicographical order)

Everything is good, to generate yourself further, BUT! When I checked this approach, it turned out that not everyone, for example, the fives, is generated this way.

[[ABC], [ABD], [ACD], [BCE], [BDE]]
[[ABC], [ABD], [ACD], [BCE], [BDF]]
[[ABC], [ABD], [ACD], [BCE], [BEF]]
[[ABC], [ABD], [ACE], [ADE], [BCF]]
[[ABC], [ABD], [ACE], [ADF], [AEF]]
[[ABC], [ABD], [ACE], [ADF], [AEG]]
[[ABC], [ABD], [ACE], [ADF], [BCG]]
[[ABC], [ABD], [ACE], [ADF], [CEG]]
[[ABC], [ABD], [ACE], [BDE], [CDE]]
[[ABC], [ABD], [ACE], [BDF], [CEG]]

If you look closely, the penultimate five turned out to be two triangles different from all fours. In terms of topology, this is “Möbius strip”. And if you try to draw it without one, any triangle, then it will be a situation when the groups of triangles are in contact with only one vertex, which is absolutely not good.

Well, there is still a way out. We take all the resulting combinations for N, pinch off one triangle from the end, “rehearse” all the other two options and check. All the same, a bunch of times faster than with combinatorial brute force.
But no, when N = 8, a triangulation was found, which differs from all sevens not by 2, but by 3 triangles.

So, starting with N = 9, 2 triangles are already pinned off, and three are “generated”. This made it possible to calculate almost all the variants up to N = 11 and the beginning of 12 (almost because there most likely there are glues that differ by 3 or even more triangles). Given that I have parallelized the whole thing. One thread I perform a primary check of gluing, the other 3 are engaged in cutting off duplicates, since isomorphism checking graphs is quite resource-intensive.

In general, if you don’t need all the options, you can pinch off (or don’t pinch) and generate the remaining ones, this will be bad, of course, but it will definitely give some options even for large N. Because it’s completely incomprehensible how much and when »To get the whole set of valid gluing.

But the whole is interesting!

I was already looking for material on brute-force graphing, and what I didn’t think about, there are no ideas even better than the iterative method. Maybe you will have thoughts on this topic?

For example, when a combination of triangles is generated, the first one always goes something like this:

ABC ABD ABE ABF ABG ...
It can be seen that AB is repeated more than 2 times. If it were possible to generate variants where initially there would not be such cases, then, in theory, the combinatorial variant would be simpler, but I have no idea how to generate such sequences.

PS it is necessary for scientific work on the classification of surfaces. Of course, they will not offend me if I provide data up to N = 11, they don’t have such data either (although, for example, a torus can be constructed from 14 triangles, I still need to cheat this for a year). But it would be interesting to think of a way that would allow N to move it away. Thanks for attention.

UPD

It was worth it before, but only now. When we split a pair of triangles from gluing from N, we get a bunch of explicit duplicates that can be removed even before the start of the search for N + 1. A good boost in speed is obtained