Knapsack problem and gray code
Not so long ago on Habré was the article " Gray Codes and brute force tasks ." This article is rather mathematical, rather than programmer, and for me, as a simple programmer, it was unbearably hard to read. But the topic itself is familiar to me, so I decided to describe it with my own view, as well as tell about how I used it in solving the knapsack problem.

KDPV: a knapsack problem on a live example
It all started 10 years ago when I was in the ninth grade. I accidentally overheard the conversation of a computer science teacher telling a problem to some of the seniors: a set of numbers was given, and another number — the control number. It is necessary to find the maximum sum of numbers from the set that would not exceed the control number.
')
The task for some reason sunk into my soul. After returning home, I quickly rolled the solution: a naive enumeration of all possible sums with the choice of the best. I received the combinations by sorting through all the N-bit binary numbers and taking the sums of those initial numbers to which the units correspond. But I was disappointed to find that with the number of elements starting somewhere around 30, the program works for a very long time. It is not surprising, since the running time of such an algorithm is n * 2 n (the number of combinations multiplied by the sum length).
5 years later. I managed to finish school and go to university, but this task was still with me. Once, leafing through the book “Algorithmic Tricks for Programmers” (Hacker's Delight / Henry S. Warren Jr.), I came across the description of the Gray code: it is a sequence of binary numbers, each of which differs from the previous one only in one bit. “Stop!” - I thought - “It means ... Yes! This means that in the same task at each step of the search, you can not count the sum as a whole, but only add or subtract one number. ” And I immediately delved into the study of the topic.
Gray code can be constructed for the number of any digit. For one rank, it is obvious:
0
one
To add a second bit, you can add the same back to this sequence.
0
one
one
0
and add units to the second half:
00
01
eleven
ten
Similarly for three discharges:
000
001
011
010
110
111
101
100
Such a code obtained by reflection of a code of lower bitness is called a reflex (reflected) gray code. There are other sequences, but in practice this one is usually used.
This code is named after Frank Gray , who invented the tube ADC, which generated the digital signal in this particular code. With small changes in the input signal level, the digital output could change only in one bit, and this excluded sharp jumps due to non-simultaneous switching of bits.
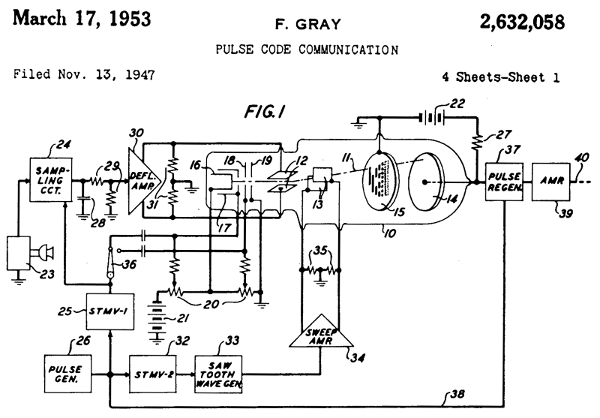
Illustration of Frank Gray's patent
The most obvious application of the Gray code is in the rotation angle sensors. A sensor similar to those in old mechanical mice, but determining not the relative offset, but the absolute value of the angle. For this, each sensor requires several optocouplers and several slotted grids. Moreover, each next position of the sensor should differ from the previous one only by the state of one bit, otherwise asynchronous switching of bits is possible at the boundaries, and consequently there are sharp jumps in the instrument readings. Here you can see a curious feature of the Gray code: the last number also differs from the first one in one bit, so it can be looped.

Sensor absolute angle of rotation. Optical slits are located in accordance with the gray code.
But back to the knapsack problem. The standard formula gives us Gray code by number:
According to it, we can only calculate the sum of all the necessary elements. And we were going to add or subtract one value at each iteration, right? So, we need to get the numbers of mutable bits. For multi-digit numbers, these numbers will be:
0
one
0
2
0
one
0
3
0
one
0
2
0
one
0
four
...
Nothing like? This is the bit number that we set to one when we simply list the usual binary numbers. Or else - the number of the lowest unit in binary. This operation is called find first set and in most processors exists as a separate instruction. Visual C ++ provides this instruction as a _BitScanForward function.
So, now we are ready to write a program that solves the knapsack problem through Gray code. We formulate the problem as follows:
We will keep the bit mask of used items, and add or remove one of them as needed. To do int-s, we limit the number of things (and used bits) to thirty-one.
I apologize for possible roughness; Unfortunately, C ++ has not been my profile language for a long time.
It works really faster than the assembly from scratch of all amounts, the difference is noticeable already at 20 numbers, and at 30 I did not wait for the naive algorithm to execute, while the new version is executed in 7 seconds. However, given the exponential complexity, this is not at all small: for 50 numbers, using this algorithm no longer makes sense. Unfortunately, any exact algorithm will not work faster than 2 n ; Faster possible is only an approximate solution. (Update: in some cases, dynamic programming and meet-in-the-middle solve the problem faster; see the comments for more details.)
Perhaps that is why I am doomed to carry my pack to the end of my life, trying to speed up this program. I already once rewrote the cycle in assembler, having received a small increase in speed, and now I'm even thinking of making a multi-threaded version of the program. You can only sympathize with me. :)

KDPV: a knapsack problem on a live example
Prehistory
It all started 10 years ago when I was in the ninth grade. I accidentally overheard the conversation of a computer science teacher telling a problem to some of the seniors: a set of numbers was given, and another number — the control number. It is necessary to find the maximum sum of numbers from the set that would not exceed the control number.
')
The task for some reason sunk into my soul. After returning home, I quickly rolled the solution: a naive enumeration of all possible sums with the choice of the best. I received the combinations by sorting through all the N-bit binary numbers and taking the sums of those initial numbers to which the units correspond. But I was disappointed to find that with the number of elements starting somewhere around 30, the program works for a very long time. It is not surprising, since the running time of such an algorithm is n * 2 n (the number of combinations multiplied by the sum length).
5 years later. I managed to finish school and go to university, but this task was still with me. Once, leafing through the book “Algorithmic Tricks for Programmers” (Hacker's Delight / Henry S. Warren Jr.), I came across the description of the Gray code: it is a sequence of binary numbers, each of which differs from the previous one only in one bit. “Stop!” - I thought - “It means ... Yes! This means that in the same task at each step of the search, you can not count the sum as a whole, but only add or subtract one number. ” And I immediately delved into the study of the topic.
Building Gray Code
Gray code can be constructed for the number of any digit. For one rank, it is obvious:
0
one
To add a second bit, you can add the same back to this sequence.
0
one
one
0
and add units to the second half:
00
01
eleven
ten
Similarly for three discharges:
000
001
011
010
110
111
101
100
Such a code obtained by reflection of a code of lower bitness is called a reflex (reflected) gray code. There are other sequences, but in practice this one is usually used.
This code is named after Frank Gray , who invented the tube ADC, which generated the digital signal in this particular code. With small changes in the input signal level, the digital output could change only in one bit, and this excluded sharp jumps due to non-simultaneous switching of bits.

Illustration of Frank Gray's patent
The most obvious application of the Gray code is in the rotation angle sensors. A sensor similar to those in old mechanical mice, but determining not the relative offset, but the absolute value of the angle. For this, each sensor requires several optocouplers and several slotted grids. Moreover, each next position of the sensor should differ from the previous one only by the state of one bit, otherwise asynchronous switching of bits is possible at the boundaries, and consequently there are sharp jumps in the instrument readings. Here you can see a curious feature of the Gray code: the last number also differs from the first one in one bit, so it can be looped.

Sensor absolute angle of rotation. Optical slits are located in accordance with the gray code.
Application in the knapsack problem
But back to the knapsack problem. The standard formula gives us Gray code by number:
G = i ^ (i >> 1) According to it, we can only calculate the sum of all the necessary elements. And we were going to add or subtract one value at each iteration, right? So, we need to get the numbers of mutable bits. For multi-digit numbers, these numbers will be:
0
one
0
2
0
one
0
3
0
one
0
2
0
one
0
four
...
Nothing like? This is the bit number that we set to one when we simply list the usual binary numbers. Or else - the number of the lowest unit in binary. This operation is called find first set and in most processors exists as a separate instruction. Visual C ++ provides this instruction as a _BitScanForward function.
So, now we are ready to write a program that solves the knapsack problem through Gray code. We formulate the problem as follows:
In the file input.txt, the capacity of the backpack is indicated in the first line, and the dimensions of things in the other lines. In the console you need to display the maximum load of the backpack and the size of the selected items. Checking the correctness of the input, etc. - see.
We will keep the bit mask of used items, and add or remove one of them as needed. To do int-s, we limit the number of things (and used bits) to thirty-one.
#include <iostream> #include <fstream> #include <bitset> #include <intrin.h> using namespace std; void main() { int target; // int nItems = 0; // int weight[31]; // ifstream inFile("input.txt"); inFile >> target; while(inFile >> weight[nItems]) nItems++; inFile.close(); const unsigned int nIterations = 1 << nItems; // , 2^n int sum = 0; // int bestSum = 0; // ( ) bitset<31> mask; // bitset<31> bestMask; // for (unsigned int i = 1; i < nIterations; i++) { unsigned long position; // _BitScanForward(&position, i); mask[position] = !mask[position]; if (mask[position]) // sum += weight[position]; else sum -= weight[position]; if (sum > target) // continue; if (sum > bestSum) // ! ... { bestSum = sum; bestMask = mask; } } cout << "Best approximation: " << bestSum << endl; cout << "Used weights:" << endl; for (int i = 0; i < 31; i++) if (bestMask[i]) cout << weight[i] << endl; cin.get(); } I apologize for possible roughness; Unfortunately, C ++ has not been my profile language for a long time.
It works really faster than the assembly from scratch of all amounts, the difference is noticeable already at 20 numbers, and at 30 I did not wait for the naive algorithm to execute, while the new version is executed in 7 seconds. However, given the exponential complexity, this is not at all small: for 50 numbers, using this algorithm no longer makes sense. Unfortunately, any exact algorithm will not work faster than 2 n ; Faster possible is only an approximate solution. (Update: in some cases, dynamic programming and meet-in-the-middle solve the problem faster; see the comments for more details.)
Perhaps that is why I am doomed to carry my pack to the end of my life, trying to speed up this program. I already once rewrote the cycle in assembler, having received a small increase in speed, and now I'm even thinking of making a multi-threaded version of the program. You can only sympathize with me. :)
Source: https://habr.com/ru/post/203362/
All Articles