Automatic spell checker, model Noisy Channel

Good day. The other day I had a task to implement the algorithm for post-processing the results of optical text recognition. To solve this problem, one of the models for checking spelling in the text was not bad, although of course slightly modified under the context of the problem. This post will be devoted to the Noisy Channel model , which allows you to perform automatic spell checking, we will study the mathematical model, write some code on c #, train the model based on Peter Norvig , and finally test what we will have.

Mathematical model - 1

To begin with the formulation of the problem. So you want to write some word w consisting of m letters, but in some way unknown to you on paper comes out the word x consisting of n letters. By the way, you are the very noisy channel , the information transfer channel with noises, which distorted the correct word w (from the universe of correct words) to an incorrect x (the set of all written words).
')

We want to find the word that you most likely meant when you wrote the word x . Let us write this thought mathematically, the model in its idea is similar to the model of the naive Bayes classifier , although even simpler:

V is a list of all natural language words.

Next, using the Bayes theorem, we expand the cause and effect, we can remove the total probability x from the denominator, since he argmax does not depend on w :

P (w) is the a priori probability of the word w in the language; this member is a statistical model of a natural language ( language model ), we will use the unigram model , although of course you have the right to use more complex models; also note that the value of this member is easily calculated from the base of words of the language;
P (x | w) is the probability that the correct word w was mistakenly written as x , this member is called the channel model ; in principle, possessing a sufficiently large base, which contains all the ways to make a mistake when writing each word of a language, then the calculation of this term would not cause difficulties, but unfortunately there is no such large base, but there are similar smaller bases, so you have to get it out (for example here is the base of 333333 words of the English language, and only for 7481 there are words with errors).

Calculation of the probability value P (x | w)

This is where Damerau-Levenshtein distance comes to help - this is a measure between two sequences of characters, defined as the minimum number of operations to insert, delete, replace and swap adjacent characters to bring the source string to the target string. We will further use the Levenshtein distance , which is distinguished by the fact that it does not support the operation of permuting neighboring symbols, so it will be easier. Both of these algorithms with examples are well described in here , so I will not repeat, but I will immediately give the code:

Levenshtein distance

public static int LevenshteinDistance(string s, string t) { int[,] d = new int[s.Length + 1, t.Length + 1]; for (int i = 0; i < s.Length + 1; i++) { d[i, 0] = i; } for (int j = 1; j < t.Length + 1; j++) { d[0, j] = j; } for (int i = 1; i <= s.Length; i++) { for (int j = 1; j <= t.Length; j++) { d[i, j] = (new int[] { d[i - 1, j] + 1, // del d[i, j - 1] + 1, // ins d[i - 1, j - 1] + (s[i - 1] == t[j - 1] ? 0 : 1) // sub }).Min(); } } return d[s.Length, t.Length]; }

This function tells us how many deletions, insertions and replacements need to be done to bring one word to another, but this is not enough for us, but I would like to receive a list of these very operations, let's call it the backtrace of the algorithm. We need to modify the above code so that when calculating the distance matrix d , the operation matrix b is also recorded. Consider an example for the words ca and abc :

d	b (0 - delete from source , left; 1 - insert from target to source ; 2 - replace symbol in source with symbol from target )

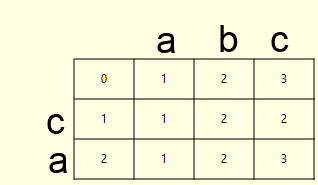As you remember, the value of the cell (i, j) in the distance matrix d is calculated as follows:

 d[i, j] = (new int[] { d[i - 1, j] + 1, // del - 0 d[i, j - 1] + 1, // ins - 1 d[i - 1, j - 1] + (s[i - 1] == t[j - 1] ? 0 : 1) // sub - 2 }).Min();

It remains for us to write the operation index in the cell (i, j) of the matrix of operations b (0 for deletion, 1 for insertion and 2 for replacement), respectively, this piece of code is converted as follows:

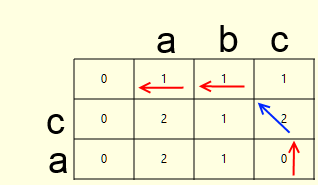
 IList<int> vals = new List<int>() { d[i - 1, j] + 1, // del d[i, j - 1] + 1, // ins d[i - 1, j - 1] + (s[i - 1] == t[j - 1] ? 0 : 1) // sub }; d[i, j] = vals.Min(); int idx = vals.IndexOf(d[i, j]); b[i, j] = idx;

Once both matrices are filled, it is not difficult to calculate the backtrace (arrows in the pictures above). This is the path from the lower right cell of the matrix of operations, along the path of the lowest cost matrix of distances. We describe the algorithm:

let's denote the bottom right cell as the current one
do one of the following
- if deletion, then write the deleted character, and move the current cell up (red arrow)
- if insert, then write the inserted symbol and shift the current cell to the left (red arrow)
- if the replacement, as well as the replaced characters are not equal, then write the replaced characters and shift the current cell to the left and up (red arrow)
- if replacement, but replaceable characters are equal, then just move the current cell to the left and up (blue arrow)
if the number of recorded operations is not equal to the Levenshtein distance, then one point back, otherwise stop

As a result, we obtain the following function, which calculates the Levenshtein distance, as well as the backtrace:

Levenshtein distance with backtrace

 //del - 0, ins - 1, sub - 2 public static Tuple<int, IList<Tuple<int, string>>> LevenshteinDistanceWithBacktrace(string s, string t) { int[,] d = new int[s.Length + 1, t.Length + 1]; int[,] b = new int[s.Length + 1, t.Length + 1]; for (int i = 0; i < s.Length + 1; i++) { d[i, 0] = i; } for (int j = 1; j < t.Length + 1; j++) { d[0, j] = j; b[0, j] = 1; } for (int i = 1; i <= s.Length; i++) { for (int j = 1; j <= t.Length; j++) { IList<int> vals = new List<int>() { d[i - 1, j] + 1, // del d[i, j - 1] + 1, // ins d[i - 1, j - 1] + (s[i - 1] == t[j - 1] ? 0 : 1) // sub }; d[i, j] = vals.Min(); int idx = vals.IndexOf(d[i, j]); b[i, j] = idx; } } List<Tuple<int, string>> bt = new List<Tuple<int, string>>(); int x = s.Length; int y = t.Length; while (bt.Count != d[s.Length, t.Length]) { switch (b[x, y]) { case 0: x--; bt.Add(new Tuple<int, string>(0, s[x].ToString())); break; case 1: y--; bt.Add(new Tuple<int, string>(1, t[y].ToString())); break; case 2: x--; y--; if (s[x] != t[y]) { bt.Add(new Tuple<int, string>(2, s[x] + "" + t[y])); } break; } } bt.Reverse(); return new Tuple<int, IList<Tuple<int, string>>>(d[s.Length, t.Length], bt); }

This function returns a tuple, in the first element of which the Levenshtein distance is written, and in the second one there is a list of <operation id, string> pairs, the string consists of one character for delete and insert operations, and two characters for replace operation (the first character is replaced by the second character ).

PS: an attentive reader will notice that there are often several ways to move along the lowest cost path from the lower right cell, this is one of the ways to increase the sample, but we will also omit it for simplicity.

Mathematical model - 2

Now we will describe the result obtained above in the language of formulas. For two words x and w, we can calculate the list of operations necessary to bring the first word to the second, we denote the list of operations with the letter f , then the probability of writing the word x as w will be equal to the probability of producing the entire list of errors f , provided that we wrote exactly x , implied w :

This is where simplifications begin, similar to those in the naive Bayes classifier :

the order of the error operations does not matter
the error will not depend on what word we wrote and on what we meant

Now, in order to calculate the error probabilities (no matter in which words they were made), it is enough to have on your hands any base of words with their erroneous writing. Let's write the final formula, in order to avoid working with numbers close to zero, we will work in the log space:

So what do we have? If we have enough texts in our hands, we can calculate a priori probabilities of words in a language; also having on hand a base of words with their wrong spelling, we can calculate the error probabilities, these two bases are enough to implement the model.

Blur error probability

When running on all the base words with argmax , we never stumble on words with zero probability. But when calculating editing operations to bring the word x to the word w , such operations may occur that were not encountered in our database of errors. In this case, additive smoothing or Laplace blur will help us (it was also used in the naive Bayes classifier ). Let me remind the formula in the context of the current task. If some correction operation f occurs in the database n times, while the total errors are in the base m , and the correction types t (for example, to replace, not how many times does the replacement " a to b " occur, but how many unique pairs "* to * "), the fuzzy probability is as follows, where k is the blurring coefficient:

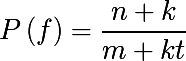
Then the probability of an operation that has never been met in the training database ( n = 0 ) will be equal to:

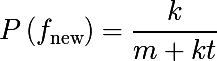
Speed

A natural question arises, what about the speed of the algorithm, because we will have to run through the entire database of words, and these are hundreds of thousands of calls to the Levenshtein distance calculation function with backtrace, and also to calculate the error probability for all words (the sum of numbers, if you keep in the database are precomputed logarithms). Here comes the following statistical fact:

80% of all printed errors are within 1 editing operation, i.e. Levenshtein distances equal to one
almost all printing errors are within 2 editing operations

Well, then you can come up with various algorithmic tricks. I used an obvious and very simple way to speed up the work of the algorithm. Obviously, if I need only words in no more than t editing operations from the current word, then their length differs from the current one by no more than t. When I initialize a class, I create a hash table, in which the keys are the length of words, and the values are sets of words of this length, this allows us to significantly reduce the search space.

Code

I will give the code of the NoisyChannel class, which I got:

NoisyChannel

 public class NoisyChannel { #region vars private string[] _words = null; private double[] _wLogPriors = null; private IDictionary<int, IList<int>> _wordLengthDictionary = null; //length of word - word indices private IDictionary<int, IDictionary<string, double>> _mistakeLogProbs = null; private double _lf = 1d; private IDictionary<int, int> _mNorms = null; #endregion #region ctor public NoisyChannel(string[] words, long[] wordFrequency, IDictionary<int, IDictionary<string, int>> mistakeFrequency, int mistakeProbSmoothing = 1) { _words = words; _wLogPriors = new double[_words.Length]; _wordLengthDictionary = new SortedDictionary<int, IList<int>>(); double wNorm = wordFrequency.Sum(); for (int i = 0; i < _words.Length; i++) { _wLogPriors[i] = Math.Log((wordFrequency[i] + 0d)/wNorm); int wl = _words[i].Length; if (!_wordLengthDictionary.ContainsKey(wl)) { _wordLengthDictionary.Add(wl, new List<int>()); } _wordLengthDictionary[wl].Add(i); } _lf = mistakeProbSmoothing; _mistakeLogProbs = new Dictionary<int, IDictionary<string, double>>(); _mNorms = new Dictionary<int, int>(); foreach (int mType in mistakeFrequency.Keys) { int mNorm = mistakeFrequency[mType].Sum(m => m.Value); _mNorms.Add(mType, mNorm); int mUnique = mistakeFrequency[mType].Count; _mistakeLogProbs.Add(mType, new Dictionary<string, double>()); foreach (string m in mistakeFrequency[mType].Keys) { _mistakeLogProbs[mType].Add(m, Math.Log((mistakeFrequency[mType][m] + _lf)/ (mNorm + _lf*mUnique)) ); } } } #endregion #region correction public IDictionary<string, double> GetCandidates(string s, int maxEditDistance = 2) { IDictionary<string, double> candidates = new Dictionary<string, double>(); IList<int> dists = new List<int>(); for (int i = s.Length - maxEditDistance; i <= s.Length + maxEditDistance; i++) { if (i >= 0) { dists.Add(i); } } foreach (int dist in dists) { foreach (int tIdx in _wordLengthDictionary[dist]) { string t = _words[tIdx]; Tuple<int, IList<Tuple<int, string>>> d = LevenshteinDistanceWithBacktrace(s, t); if (d.Item1 > maxEditDistance) { continue; } double p = _wLogPriors[tIdx]; foreach (Tuple<int, string> m in d.Item2) { if (!_mistakeLogProbs[m.Item1].ContainsKey(m.Item2)) { p += _lf/(_mNorms[m.Item1] + _lf*_mistakeLogProbs[m.Item1].Count); } else { p += _mistakeLogProbs[m.Item1][m.Item2]; } } candidates.Add(_words[tIdx], p); } } candidates = candidates.OrderByDescending(c => c.Value).ToDictionary(c => c.Key, c => c.Value); return candidates; } #endregion #region static helper //del - 0, ins - 1, sub - 2 public static Tuple<int, IList<Tuple<int, string>>> LevenshteinDistanceWithBacktrace(string s, string t) { int[,] d = new int[s.Length + 1, t.Length + 1]; int[,] b = new int[s.Length + 1, t.Length + 1]; for (int i = 0; i < s.Length + 1; i++) { d[i, 0] = i; } for (int j = 1; j < t.Length + 1; j++) { d[0, j] = j; b[0, j] = 1; } for (int i = 1; i <= s.Length; i++) { for (int j = 1; j <= t.Length; j++) { IList<int> vals = new List<int>() { d[i - 1, j] + 1, // del d[i, j - 1] + 1, // ins d[i - 1, j - 1] + (s[i - 1] == t[j - 1] ? 0 : 1) // sub }; d[i, j] = vals.Min(); int idx = vals.IndexOf(d[i, j]); b[i, j] = idx; } } List<Tuple<int, string>> bt = new List<Tuple<int, string>>(); int x = s.Length; int y = t.Length; while (bt.Count != d[s.Length, t.Length]) { switch (b[x, y]) { case 0: x--; bt.Add(new Tuple<int, string>(0, s[x].ToString())); break; case 1: y--; bt.Add(new Tuple<int, string>(1, t[y].ToString())); break; case 2: x--; y--; if (s[x] != t[y]) { bt.Add(new Tuple<int, string>(2, s[x] + "" + t[y])); } break; } } bt.Reverse(); return new Tuple<int, IList<Tuple<int, string>>>(d[s.Length, t.Length], bt); } public static int LevenshteinDistance(string s, string t) { int[,] d = new int[s.Length + 1, t.Length + 1]; for (int i = 0; i < s.Length + 1; i++) { d[i, 0] = i; } for (int j = 1; j < t.Length + 1; j++) { d[0, j] = j; } for (int i = 1; i <= s.Length; i++) { for (int j = 1; j <= t.Length; j++) { d[i, j] = (new int[] { d[i - 1, j] + 1, // del d[i, j - 1] + 1, // ins d[i - 1, j - 1] + (s[i - 1] == t[j - 1] ? 0 : 1) // sub }).Min(); } } return d[s.Length, t.Length]; } #endregion }

The class is initialized with the following parameters:

string [] words - a list of words in a language;
long [] wordFrequency - word frequency;
IDictionary <int, IDictionary <string, int >> mistakeFrequency
int mistakeProbSmoothing = 1 - error rate blur rate

Testing

For testing, we use Peter Norvig's database , which contains 333333 words with frequencies, as well as 7481 words with erroneous spellings. The following code is used to calculate the values required for the initialization of the NoisyChannel class:

reading base

 string[] words = null; long[] wordFrequency = null; #region read priors if (!File.Exists("../../../Data/words.bin") || !File.Exists("../../../Data/wordFrequency.bin")) { IDictionary<string, long> wf = new Dictionary<string, long>(); Console.Write("Reading data:"); using (StreamReader sr = new StreamReader("../../../Data/count_1w.txt")) { string line = sr.ReadLine(); while (line != null) { string[] parts = line.Split('\t'); wf.Add(parts[0].Trim(), Convert.ToInt64(parts[1])); line = sr.ReadLine(); Console.Write("."); } sr.Close(); } Console.WriteLine("Done!"); words = wf.Keys.ToArray(); wordFrequency = wf.Values.ToArray(); using (FileStream fs = File.Create("../../../Data/words.bin")) { BinaryFormatter bf = new BinaryFormatter(); bf.Serialize(fs, words); fs.Flush(); fs.Close(); } using (FileStream fs = File.Create("../../../Data/wordFrequency.bin")) { BinaryFormatter bf = new BinaryFormatter(); bf.Serialize(fs, wordFrequency); fs.Flush(); fs.Close(); } } else { using (FileStream fs = File.OpenRead("../../../Data/words.bin")) { BinaryFormatter bf = new BinaryFormatter(); words = bf.Deserialize(fs) as string[]; fs.Close(); } using (FileStream fs = File.OpenRead("../../../Data/wordFrequency.bin")) { BinaryFormatter bf = new BinaryFormatter(); wordFrequency = bf.Deserialize(fs) as long[]; fs.Close(); } } #endregion //del - 0, ins - 1, sub - 2 IDictionary<int, IDictionary<string, int>> mistakeFrequency = new Dictionary<int, IDictionary<string, int>>(); #region read mistakes IDictionary<string, IList<string>> misspelledWords = new SortedDictionary<string, IList<string>>(); using (StreamReader sr = new StreamReader("../../../Data/spell-errors.txt")) { string line = sr.ReadLine(); while (line != null) { string[] parts = line.Split(':'); string wt = parts[0].Trim(); misspelledWords.Add(wt, parts[1].Split(',').Select(w => w.Trim()).ToList()); line = sr.ReadLine(); } sr.Close(); } mistakeFrequency.Add(0, new Dictionary<string, int>()); mistakeFrequency.Add(1, new Dictionary<string, int>()); mistakeFrequency.Add(2, new Dictionary<string, int>()); foreach (string s in misspelledWords.Keys) { foreach (string t in misspelledWords[s]) { var d = NoisyChannel.LevenshteinDistanceWithBacktrace(s, t); foreach (Tuple<int, string> ml in d.Item2) { if (!mistakeFrequency[ml.Item1].ContainsKey(ml.Item2)) { mistakeFrequency[ml.Item1].Add(ml.Item2, 0); } mistakeFrequency[ml.Item1][ml.Item2]++; } } } #endregion

The following code initializes the model and searches for the correct words for the word " he ;; o " (of course, hello is implied, dotted -comma is to the right of l and it was easy to make a mistake when typing, the word hello does not contain the word he; ; o ) at a distance of not more than 2, with the time detection:

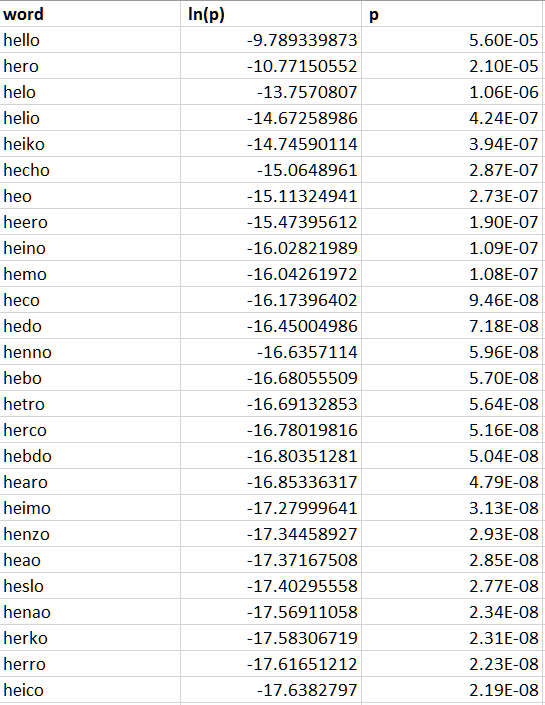
 NoisyChannel nc = new NoisyChannel(words, wordFrequency, mistakeFrequency, 1); Stopwatch timer = new Stopwatch(); timer.Start(); IDictionary<string, double> c = nc.GetCandidates("he;;o", 2); timer.Stop(); TimeSpan ts = timer.Elapsed; Console.WriteLine(ts.ToString());

In my opinion, such a calculation takes on average a little less than 1 second, although of course the optimization process is not exhausted by the above methods, but on the contrary, it only begins with them. Take a look at the replacement options and their probabilities:

Links

Archive code can be merged from here .

Source: https://habr.com/ru/post/202908/

All Articles