Cache-Conscious Binary Search
Consider a simple task: there is some fairly large, unchanging set of numbers, there are many requests for the presence of a certain number in this set, you need to process these requests as quickly as possible. One of the classic solutions is to form a sorted array and process queries through a binary search. But is it possible to achieve higher performance than in the classical implementation? In this article I would like to tell you about Cache-Conscious Binary Search. In this algorithm, it is proposed to reorder the elements of the array so that the use of the processor cache is as efficient as possible.
Disclaimer: I'm not trying to create the most effective solution to this problem. I would just like to discuss the approach to building data structures based on the peculiarities of working with the processor cache, since Many in solving optimization problems, in principle, do not think about the processor architecture. I am also not going to write an ideal implementation of Cache-Conscious Binary Search, I would like to see the effect of this approach on a fairly simple example (also in order to simplify the code, the number of vertices is taken equal to N = 2 ^ K-1). As a programming language, I will use C # (the overall speed for us is not critical, since the main focus is not on creating the fastest program in the world, but on a relative comparison of different approaches to solving the problem). It is also worth noting that the algorithm is effective only on large arrays; therefore, this approach should not be used in all tasks; you must first make sure that it is expedient. It is assumed that the reader has a basic understanding of what the processor cache is and how it works.
Consider the classic implementation of a binary search: suppose we have a sorted array

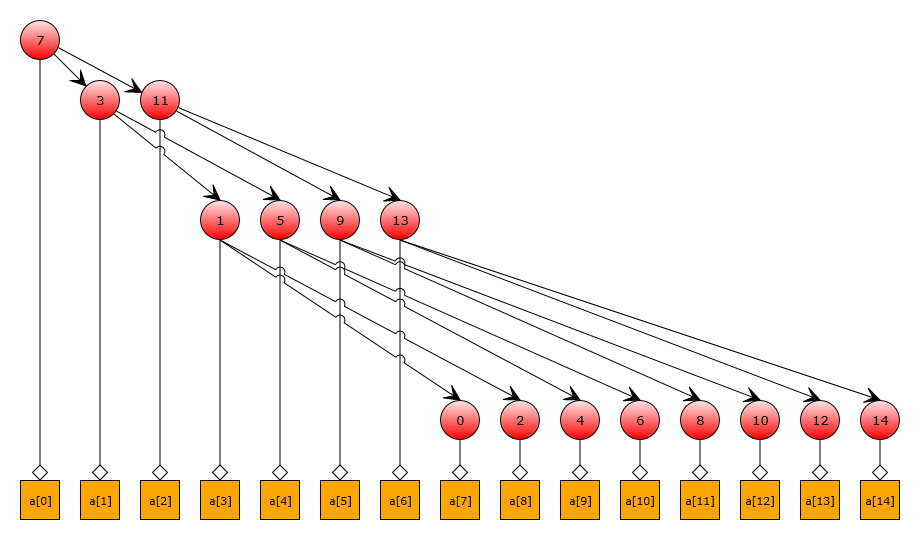
From the figure it is clear that when passing through such a tree, there will first be an appeal to the 7th element, and then (in the case of
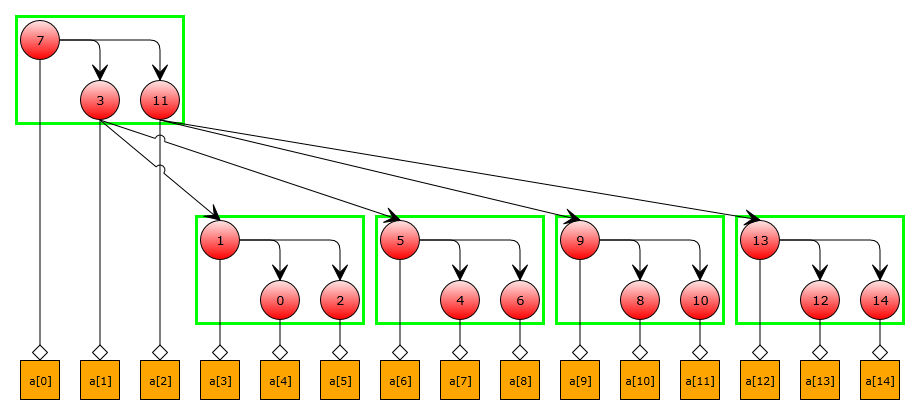
Now the elements of the array, to which we will address at the first iterations, are close to each other. But with the growth of the iteration number, we still get a large amount of cache miss-s. To correct this situation, we divide our “big” binary search tree into small subtrees. Each such subtree will correspond to several levels of the original tree, and the elements of the subtree will be located close to each other. Thus, the cache miss will be formed mainly during the transition to the next subtree. The height of the subtree can be varied by selecting it in accordance with the processor architecture. We illustrate these constructions in our example, taking the height of the subtree to be 2:
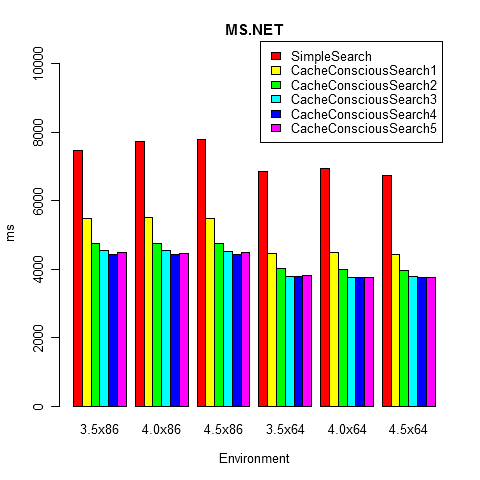
And now for the practical research. For the purity of the experiment and obtain accurate results, we will measure the time using the BenchmarkDotNet project. Consider the most trivial implementation of the considered algorithm without any additional optimizations (the source code is provided on GitHub). We will compare the classical implementation and the cache-conscious-implementation with different subtree heights (CacheConsciousSearchK corresponds to a subtree with height K). We take the tree height to 24. On my machine (Intel Core i7-3632QM CPU 2.20GHz) the following results were obtained (the algorithm is very sensitive to the processor architecture, so you can get completely different time estimates):
Under Mono 3.3.0, the results were also similar:
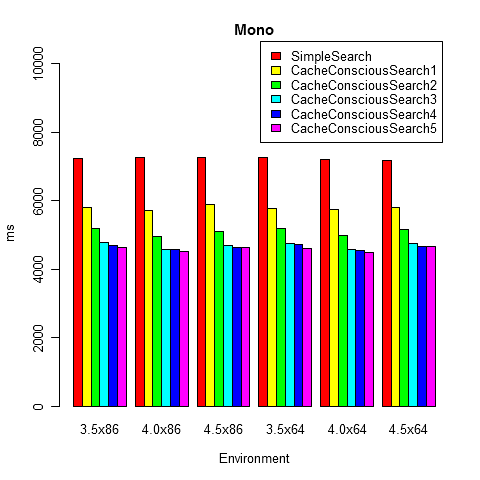
From these pictures it is clear that the classic implementation of binary search is significantly inferior to the Cache-Conscious implementation. It should be noted that at first, as the height of subtrees grows, speed increases, but this trend is not long observed (subtrees start to bring little benefit if a large amount of cashe miss-s occurs inside the subtree).
')
Of course, Cache-Conscious Binary Search is just an example of how a program can be adapted to the features of the processor cache. Such Cache-Conscious Data Structures can be invaluable in optimizing an application if your data structures are large enough, and consecutive requests to them fall on different parts of the memory. But you shouldn’t rush to rewrite everything under Cache-Conscious: remember that the code will become much more complicated, and the increase in efficiency largely depends on the processor architecture used. In real life, it is better to first think about choosing the most optimal algorithms with good asymptotics, different presuppositions, heuristics, etc., and save Cache-Conscious for times when everything will become very bad.
Quick applications to you!
You can also read on the topic:
Update. Addition from MikeMirzayanov : There is such a trick. If it is necessary to search by binpoisk in an array of length n, then it can be divided into sqrt (n) blocks by sqrt (n) elements. Then, by searching for log (sqrt (n)), find the necessary block and find the element in it by the second binary search for log (sqrt (n)). In sum, it turns out all the same log (n), but the cache hits much more, because every time we look for a rather short array of length sqrt (n).
Disclaimer: I'm not trying to create the most effective solution to this problem. I would just like to discuss the approach to building data structures based on the peculiarities of working with the processor cache, since Many in solving optimization problems, in principle, do not think about the processor architecture. I am also not going to write an ideal implementation of Cache-Conscious Binary Search, I would like to see the effect of this approach on a fairly simple example (also in order to simplify the code, the number of vertices is taken equal to N = 2 ^ K-1). As a programming language, I will use C # (the overall speed for us is not critical, since the main focus is not on creating the fastest program in the world, but on a relative comparison of different approaches to solving the problem). It is also worth noting that the algorithm is effective only on large arrays; therefore, this approach should not be used in all tasks; you must first make sure that it is expedient. It is assumed that the reader has a basic understanding of what the processor cache is and how it works.
Consider the classic implementation of a binary search: suppose we have a sorted array
a and some element x , which we will look for in it: public bool Contains(int x) { int l = 0, r = N - 1; while (l <= r) { int m = (l + r) / 2; if (a[m] == x) return true; if (a[m] > x) r = m - 1; else l = m + 1; } return false; } In this implementation, at the first iterations of the algorithm, requests will be made to the array elements that are far from each other. Draw a search tree for an array of 15 elements:
From the figure it is clear that when passing through such a tree, there will first be an appeal to the 7th element, and then (in the case of
a[7]!=x ) to the 3rd or 11th. On such a small array, this is not critical, but in a large array, these references will correspond to different lines of the processor cache, which will adversely affect performance. Let's try to reorder the elements so that successive accesses to the array fall into close memory areas. As a first approximation, you can try to arrange each level of the tree one after another with a simple wide search. On our test tree we get the following result:
Now the elements of the array, to which we will address at the first iterations, are close to each other. But with the growth of the iteration number, we still get a large amount of cache miss-s. To correct this situation, we divide our “big” binary search tree into small subtrees. Each such subtree will correspond to several levels of the original tree, and the elements of the subtree will be located close to each other. Thus, the cache miss will be formed mainly during the transition to the next subtree. The height of the subtree can be varied by selecting it in accordance with the processor architecture. We illustrate these constructions in our example, taking the height of the subtree to be 2:

And now for the practical research. For the purity of the experiment and obtain accurate results, we will measure the time using the BenchmarkDotNet project. Consider the most trivial implementation of the considered algorithm without any additional optimizations (the source code is provided on GitHub). We will compare the classical implementation and the cache-conscious-implementation with different subtree heights (CacheConsciousSearchK corresponds to a subtree with height K). We take the tree height to 24. On my machine (Intel Core i7-3632QM CPU 2.20GHz) the following results were obtained (the algorithm is very sensitive to the processor architecture, so you can get completely different time estimates):
// Microsoft.NET 4.5 x64 SimpleSearch : 6725ms CacheConsciousSearch1 : 4428ms CacheConsciousSearch2 : 3963ms CacheConsciousSearch3 : 3778ms CacheConsciousSearch4 : 3774ms CacheConsciousSearch5 : 3762ms Benchmark source code
Just in case, I launched a benchmark under different versions of the .NET Framework and with different bit depths. All configurations gave similar results: public class CacheConsciousBinarySearchCompetition : BenchmarkCompetition { private const int K = 24, N = (1 << K) - 1, IterationCount = 10000000; private readonly Random random = new Random(); private Tree originalTree; private int[] bfs; protected override void Prepare() { originalTree = new Tree(Enumerable.Range(0, N).Select(x => 2 * x).ToArray()); bfs = originalTree.Bfs(); } [BenchmarkMethod] public void SimpleSearch() { SingleRun(originalTree); } [BenchmarkMethod] public void CacheConsciousSearch1() { SingleRun(new CacheConsciousTree(bfs, 1)); } [BenchmarkMethod] public void CacheConsciousSearch2() { SingleRun(new CacheConsciousTree(bfs, 2)); } [BenchmarkMethod] public void CacheConsciousSearch3() { SingleRun(new CacheConsciousTree(bfs, 3)); } [BenchmarkMethod] public void CacheConsciousSearch4() { SingleRun(new CacheConsciousTree(bfs, 4)); } [BenchmarkMethod] public void CacheConsciousSearch5() { SingleRun(new CacheConsciousTree(bfs, 5)); } private int SingleRun(ITree tree) { int searchedCount = 0; for (int iteration = 0; iteration < IterationCount; iteration++) { int x = random.Next(N * 2); if (tree.Contains(x)) searchedCount++; } return searchedCount; } interface ITree { bool Contains(int x); } class Tree : ITree { private readonly int[] a; public Tree(int[] a) { this.a = a; } public bool Contains(int x) { int l = 0, r = N - 1; while (l <= r) { int m = (l + r) / 2; if (a[m] == x) return true; if (a[m] > x) r = m - 1; else l = m + 1; } return false; } public int[] Bfs() { int[] bfs = new int[N], l = new int[N], r = new int[N]; int tail = 0, head = 0; l[head] = 0; r[head++] = N - 1; while (tail < head) { int m = (l[tail] + r[tail]) / 2; bfs[tail] = a[m]; if (l[tail] < m) { l[head] = l[tail]; r[head++] = m - 1; } if (m < r[tail]) { l[head] = m + 1; r[head++] = r[tail]; } tail++; } return bfs; } } class CacheConsciousTree : ITree { private readonly int[] a; private readonly int level; public CacheConsciousTree(int[] bfs, int level) { this.level = level; int size = (1 << level) - 1, counter = 0; a = new int[N]; var was = new bool[N]; var queue = new int[size]; for (int i = 0; i < N; i++) if (!was[i]) { int head = 0; queue[head++] = i; for (int tail = 0; tail < head; tail++) { a[counter++] = bfs[queue[tail]]; was[queue[tail]] = true; if (queue[tail] * 2 + 1 < N && head < size) queue[head++] = queue[tail] * 2 + 1; if (queue[tail] * 2 + 2 < N && head < size) queue[head++] = queue[tail] * 2 + 2; } } } public bool Contains(int x) { int u = 0, deep = 0, leafCount = 1 << (level - 1); int root = 0, rootOffset = 0; while (deep < K) { int value = a[root + u]; if (value == x) return true; if (++deep % level != 0) { if (value > x) u = 2 * u + 1; else u = 2 * u + 2; } else { int subTreeSize = (1 << Math.Min(level, K - deep)) - 1; if (value > x) rootOffset = rootOffset * leafCount * 2 + (u - leafCount + 1) * 2; else rootOffset = rootOffset * leafCount * 2 + (u - leafCount + 1) * 2 + 1; root = (1 << deep) - 1 + rootOffset * subTreeSize; u = 0; } } return false; } } } 
Under Mono 3.3.0, the results were also similar:

From these pictures it is clear that the classic implementation of binary search is significantly inferior to the Cache-Conscious implementation. It should be noted that at first, as the height of subtrees grows, speed increases, but this trend is not long observed (subtrees start to bring little benefit if a large amount of cashe miss-s occurs inside the subtree).
')
Of course, Cache-Conscious Binary Search is just an example of how a program can be adapted to the features of the processor cache. Such Cache-Conscious Data Structures can be invaluable in optimizing an application if your data structures are large enough, and consecutive requests to them fall on different parts of the memory. But you shouldn’t rush to rewrite everything under Cache-Conscious: remember that the code will become much more complicated, and the increase in efficiency largely depends on the processor architecture used. In real life, it is better to first think about choosing the most optimal algorithms with good asymptotics, different presuppositions, heuristics, etc., and save Cache-Conscious for times when everything will become very bad.
Quick applications to you!
You can also read on the topic:
- Cache Conscious Indexing for Decision-Support in Main Memory
- Cache-Conscious Data Structures
- Cache-Conscious Concurrent Data Structures
- Making B + -Trees Cache Conscious in Main Memory
Update. Addition from MikeMirzayanov : There is such a trick. If it is necessary to search by binpoisk in an array of length n, then it can be divided into sqrt (n) blocks by sqrt (n) elements. Then, by searching for log (sqrt (n)), find the necessary block and find the element in it by the second binary search for log (sqrt (n)). In sum, it turns out all the same log (n), but the cache hits much more, because every time we look for a rather short array of length sqrt (n).
Source: https://habr.com/ru/post/202820/
All Articles