Reduction of dimensions in the linear binary classification problem (eg SVM)
Required knowledge: acquaintance with the methods of linear binary classification (eg SVM (see SVM Tutorial )), linear algebra, linear programming
Consider a linear binary classification problem (if a problem is linearly inseparable, it can be reduced to that with the help of a symmetric integral L-2 kernel (see SVM )).
When solving such a problem, the classified elements (hereinafter samples) are represented as elements of the vector space of dimension n. In practice, in such problems, n can be extremely large, for example, for the task of classifying genes, it can amount to tens of thousands. The large dimension implies, besides the high computation time, the potentially high error of the numerical calculations. In addition, the use of a large dimension may require large financial costs (to conduct experiments). The question is: is it possible and how can one reduce n by discarding insignificant components of samples in such a way that samples are separated “no worse” in the new space (remain linearly separable) or “not much worse”.
In my article, I want to begin with a brief overview of the method from this article, Gene_Selection_for_Cancer_Classification_using , and then suggest my own method.
The main idea of the dimension reduction method in Gene_Selection_for_Cancer_Classification_using is to rank all components. The following algorithm is proposed:
Basically, the article discusses the method of assigning weights to the resulting SVMs. That is, we use as weights the coefficients in the classifying function of the corresponding components. Suppose after SVM training we got the classifying function (w, x) + b = 0, then wi component will be the weight of component i. The article also discusses the correlation method of defining weights, but, like any other, loses the SVM method, since when repeated in step 1, the weights in the SVM method are known from step 3.
')
The class of such algorithms is still forced to train SVMs on high-dimensional samples, i.e. problems of error and speed are not solved. All it gives is the possibility, after SVM training, to reduce the number of components of classified samples. If it is financially expensive to get the values of the reduced components experienced, then you can save.
PS In addition, the choice of scales as wi is quite controversial. I would suggest at least multiplying them by the sample variance of component i in all samples or by the first central absolute sampling moment of component i in all samples.
The idea is as follows: we discard the component and check whether now (without this component) the set of samples will be linearly separable. If yes, then do not return this component, if not then return. The question is how to test the set for linear separability?
Let xi be samples, yi be a sample belonging to a class (yi = -1 is the first class, yi = 1 is the second class) i = 1..m. Then the samples are linearly separable if
- has a non-trivial solution, where
(conditions as when training SVM).
_____________________________________________________________________________________
Let's first consider how to test the set for strict linear separability:
- has a solution. According to the Farkas lemma <=>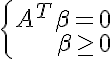
- has only a trivial solution. We check the vector 0 for optimality in the linear programming problem with the obtained constraints and the objective function
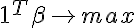If 0 was optimal, then the set is strictly linearly separable.
_____________________________________________________________________________________
Loose linear separability:
- has a non-trivial solution. According to the Farkas lemma <=>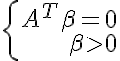
- has no solutions. <=>
- has no solutions. To check the availability of a solution to the obtained constraints, you can use any method of finding the initial reference vector in a linear programming problem with these constraints.
_____________________________________________________________________________________
In some problems (especially when the dimension (n) exceeds the number of samples (m)) we may want to discard the component only if the separation of the set occurs with a certain gap. Then you can check the following conditions:
- has a solution, where c > = 0 is the gap parameter, and the second constraint replaces the normalization alpha (so that the solution A * x > 0 cannot simply be multiplied by a sufficiently large constant k and satisfied with the system A * k * x > = c ). These conditions by the Farkas Lemma (E is the identity matrix) <=>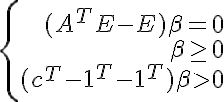
- has no solutions. We check vector 0 for optimality in a linear programming problem with the obtained constraints (without the last line) and the objective function
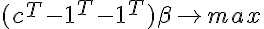If 0 was optimal, then the set can be divided with a given gap.
_____________________________________________________________________________________
In some tasks (especially when the number of samples (m) exceeds the dimension (n)) we may want to discard the component even if the separation of the set occurs with some error. Then you can check the following conditions:
- has a solution, where c <= 0 is the error parameter, and the second restrictions replace the normalization alpha (so that the solution A * x > negative_number_less_than_ c cannot be simply divided into a sufficiently large constant k and satisfy the system A * x / k> = c ). Here, everything is similar to the above case, only because of the disjunction (square bracket), we have to consider two linear programming problems.
Consider a linear binary classification problem (if a problem is linearly inseparable, it can be reduced to that with the help of a symmetric integral L-2 kernel (see SVM )).
When solving such a problem, the classified elements (hereinafter samples) are represented as elements of the vector space of dimension n. In practice, in such problems, n can be extremely large, for example, for the task of classifying genes, it can amount to tens of thousands. The large dimension implies, besides the high computation time, the potentially high error of the numerical calculations. In addition, the use of a large dimension may require large financial costs (to conduct experiments). The question is: is it possible and how can one reduce n by discarding insignificant components of samples in such a way that samples are separated “no worse” in the new space (remain linearly separable) or “not much worse”.
In my article, I want to begin with a brief overview of the method from this article, Gene_Selection_for_Cancer_Classification_using , and then suggest my own method.
Algorithms from Gene_Selection_for_Cancer_Classification_using
The main idea of the dimension reduction method in Gene_Selection_for_Cancer_Classification_using is to rank all components. The following algorithm is proposed:
- We assign all weights to all (remaining) components (about how - further)
- We throw out the component with the minimum weight of all samples.
- We train SVM. If it was not possible to separate the samples, then we return the component that was thrown out at the last step and exit the algorithm, otherwise go to step 1 with the data without the component thrown out.
Basically, the article discusses the method of assigning weights to the resulting SVMs. That is, we use as weights the coefficients in the classifying function of the corresponding components. Suppose after SVM training we got the classifying function (w, x) + b = 0, then wi component will be the weight of component i. The article also discusses the correlation method of defining weights, but, like any other, loses the SVM method, since when repeated in step 1, the weights in the SVM method are known from step 3.
')
The class of such algorithms is still forced to train SVMs on high-dimensional samples, i.e. problems of error and speed are not solved. All it gives is the possibility, after SVM training, to reduce the number of components of classified samples. If it is financially expensive to get the values of the reduced components experienced, then you can save.
PS In addition, the choice of scales as wi is quite controversial. I would suggest at least multiplying them by the sample variance of component i in all samples or by the first central absolute sampling moment of component i in all samples.
My algorithm
The idea is as follows: we discard the component and check whether now (without this component) the set of samples will be linearly separable. If yes, then do not return this component, if not then return. The question is how to test the set for linear separability?
Let xi be samples, yi be a sample belonging to a class (yi = -1 is the first class, yi = 1 is the second class) i = 1..m. Then the samples are linearly separable if
_____________________________________________________________________________________
Let's first consider how to test the set for strict linear separability:
_____________________________________________________________________________________
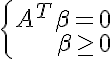
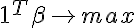
Loose linear separability:
_____________________________________________________________________________________
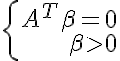
In some problems (especially when the dimension (n) exceeds the number of samples (m)) we may want to discard the component only if the separation of the set occurs with a certain gap. Then you can check the following conditions:
_____________________________________________________________________________________
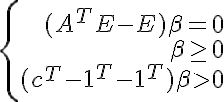
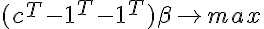
In some tasks (especially when the number of samples (m) exceeds the dimension (n)) we may want to discard the component even if the separation of the set occurs with some error. Then you can check the following conditions:
Source: https://habr.com/ru/post/202486/
All Articles