Geekly Articles each Day
📜 ⬆️ ⬇️

Personal cryptography: a story about one useful vulnerability

image
Asymmetric cryptography has become an elegant solution to key distribution. But as is often the case, what helped eliminate one problem caused another.

The public key, due to the mathematical properties of asymmetric cryptoalgorithms is a set of random bits that do not contain any information about the owner, so it can not serve as an authentication tool. This flaw has led to the emergence of a hierarchical public key certification system.
Consider how users are currently authenticated:
  1. Alice passes the verification process in the certification center (CA) and receives a certificate
  2. Alice sends her certificate to Bob
  3. Bob receives a CA certificate
  4. Using the obtained certificates, Bob authenticates Alice.

The first to think about simplifying this scheme was Adi Shamir in 1984. He suggested that if the opportunity arose to use Alice’s name or email address as a public key, this would deprive the complicated procedure of authentication of any meaning.
For a long time, Shamir's idea remained just a beautiful cryptographic puzzle, but in 2000, thanks to one known vulnerability in elliptical cryptography, the idea was brought to life.

Class of vulnerable elliptic curves


Elliptic cryptography is built on the assumption of the complexity of solving the problem of discrete logarithmization over a field of points of an elliptic curve.
The main advantage of the "elliptic" over classical asymmetric cryptography is much smaller key sizes. This is explained by the fact that for the classical discrete logarithm problem there are so-called subexponential solution algorithms that have the following computational complexity image . Therefore, to achieve durability of the order of 2 80, it is necessary that the number p be 1024 bits in size.
For the discrete logarithm problem over the points of the elliptic curve, no subexponential algorithms were found. The fastest algorithms for this type of problem have difficulty image . This allows you to use numbers as small as 160 bits to achieve the same persistence threshold of 2 80 .

Moreover, there is a special class of elliptic curves for which all of the above is not entirely true. Such curves are called super-singular . For supersingular elliptic curves, a method was found to reduce the discrete logarithm problem over points of an elliptic curve to the classical discrete logarithm problem. Accordingly, when using supersingular curves, the main advantage of elliptical cryptography becomes a big disadvantage. The small key size, which is characteristic of the “elliptic”, will allow using the subexponential algorithm with great efficiency and hacking the entire system.
')
In a little more detail I described all this in one of my recent topics Elliptical cryptography: theory . Today I want to talk about a method that makes super-singular curves so vulnerable and a protocol that turned this disadvantage into an advantage.

Weil mating


In 1983, Menezes, Okamoto and Vanstone showed that for super-singular curves there is an effective way to map pairs of points of a curve into a non-degenerate element of a finite field.
The isomorphism used by them for this is called the Weil pairing . In accordance with two points of the field E (F q l ), this isomorphism places an element of the field F q l . In other words, the Weil pairing allows us to reflect the set of points of an elliptic curve into a set of residues modulo a large number.

Let (G 1 , +) be a group of points of an elliptic curve. And (G 2 , *) is a residue group modulo a large number. And let these two groups be isomorphic with respect to the Weil mating e x . Weil mating has the following properties:
  1. Identity: for all performed
  2. Bilinearity: for all performed
  3. Nondegeneracy: For all such that performed
  4. Practical efficiency: for all P and R numbers allow efficient calculation

It follows from bilinearity that . Thus, to solve the discrete logarithm problem on elliptic curves using the Weil pairing, it is necessary to calculate a pair and . Possessing these two elements of the group G 2, one can apply a subexponential algorithm to search for n .

It is the Weil pairing that makes super-singular curves useless in EDS algorithms. On the other hand, it also helped to realize the idea of ​​Shamir.

Diffie-Hellman's decision making task


The fundamental problems of modern asymmetric cryptography on elliptic curves are:

In addition, there is another type of problems that are just as difficult to solve as the previous two, but have an effective solution for the case of supersingular curves.

The problem of making a decision Diffie-Hellman .
Four points of the curve P, aP, bP, cP are given . It is necessary to determine whether the equality a = bc holds.
Before describing how Weil pairing helps solve this problem, I note that the identity property for points P and Q , such that Q = aP , leads to a rather inconvenient result. According to this rule, the mapping of the pair P and Q equals one. .
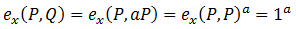To correct this deficiency, it is necessary to find another point of the same order as Q, but at the same time linearly independent of P.
There is a special method called the deforming mapping, denoted as F (P) . When using a deforming display, the Weil pairing is written as: .
Expression will not be equal to one, because the point F (P) is linearly independent of P. This operation is called the modified Weyl pairing.

Now consider the Diffie-Hellman decision problem. Calculate a pair and . Considering that , equality will be executed only under the condition that a = bc .

This feature of supersingular curves made it possible to implement the so-called non - interactive key distribution scheme. And it was a new impetus for research in the field of personal cryptography .

Personal cryptography. Non-interactive SOK key sharing scheme


We now return to the main topic of this topic. Namely, to the problem of key authentication.

In 2000, a group of researchers Sakai, Ogishi, Kasarah developed a key separation method similar to the Diffie-Hellman protocol. But different from the latter in that in order to obtain a single encryption key, Alice and Bob users do not need to exchange public keys. Instead, they use each other’s names as public keys. Due to the fact that the protocol does not provide for the participation of the second party to obtain the key, it was defined as non-interactive .

The non-interactive SOK protocol (in honor of the first letters of the names of its creators) consists of the following parts.

Setting system parameters
The protocol involves three parties: Alice, Bob and Trent (a trusted center that generates keys and identifies users).

The first part of the protocol is produced directly by Trent. It performs the following operations.
  1. Generates two groups (G 1 , +) and (G 2 , *) for which the modified Weyl pairing e is performed. And then selects an arbitrary originating element. image .
  2. Randomly selects the number l and sets the parameter P pub = l * P. The number l is the master secret key of the system.
  3. Selects a strong cryptographic hash function f. The function f is used to display the user's personal information ID, in the element of the group G 1 .
  4. He reads out the system parameters (G 1 , G 2 , e , P, P pub , f).

Generating user keys
This part is also performed by Trent. Let ID A be a uniquely identifiable Alice identifier. This can be her full name or passport information.
After verifying Alice's identity and making sure that ID A really belongs to her, Trent performs the following actions.
  1. Calculates an element of the group G 1 as P ID = f (ID A ).
  2. Sets Alice's private key S IDa = l * P IDa

It should be noted that the secrecy of Alice's private key is based on the discrete logarithm problem over points of an elliptic curve. And since we use the weak class of elliptic curves, the key sizes must be of the order of 1024 bits, as is the case with classical asymmetric cryptography.

Key Sharing Algorithm
Alice and Bob IDs ID A and ID B are known to both partners. Therefore, they can calculate the elements of the group G 1 P A = f (ID A ) and P B = f (ID B ).
To generate the shared key K AB, Alice calculates .
Bob in turn to compute a shared key with Alice .
Given the property of bilinearity, independently of each other, they receive the same element of group G 2 : .

Advantages and disadvantages of personal cryptography


Benefits
Non-interactivity inherent in personal cryptography gives them one very serious advantage. The procedure for the exchange of public keys is completely losing its relevance.
There is no need to wait for the receipt of the certificate of the other party to establish communication. It is enough to use the identity of the partner to generate a shared key.

Moreover, it enables so-called denied encryption . If Alice and Bob exchanged encrypted messages that compromised Alice, and for some reason Bob decided to divulge this correspondence, Alice can say that she did not participate in the dialogue. Since Bob could generate the shared key himself and fake Alice's messages.

disadvantages
One of them is that Trent involved in the generation of private keys will have the ability to decrypt all messages on the network. Therefore, it is likely that personal cryptography can be used only in small networks that have a certain trustee.

The second drawback is that it is still unclear what to do if the user's private key is compromised. The non-interactive key revocation task is still open.

However, despite these significant shortcomings, personal cryptography looks like a very attractive technology. And who knows how everything would turn out, if in 1984 Shamir had found such an interesting solution for his puzzle.

Source: https://habr.com/ru/post/202368/

More articles:


All Articles