We comprehend integrals using Maple
Acquainted with the magic of computer algebra systems, I spent several evenings in strange and seemingly meaningless activities - solving college problems in algebra, mathematical analysis, differential equations ... Just because it was interesting - would there be such an equation that Maple could not solve nor maxima? In my arsenal there were these two systems, and they coped with all the problems with a bang. This does not mean that everything was solved instantly and without the use of mathematical knowledge. Some tasks required special approaches, numerous transformations and change of variables. So, it is possible to argue with opponents of computer algebra - if used correctly, it does not relax the brain at all, but rather develops logical (and other) thinking.
Illustrating the above, in this post I will talk about several different scenarios for using SKA Maple in the fight against integrals. I hope that people familiar with the subtleties of symbolic calculations will find something new for themselves here. And for those to whom this way of solving problems is new, I tried to add more comments.

Anyone who is unlucky with a matan teacher, and people who just like to observe the step-by-step solution of integrals, is dedicated to a separate student package module. Some of his "chips" are good for "intricate" integrals, but more on that later.
')
So, first connect the module and limit the output of additional information. A colon at the end means that the command output will be hidden from the user's eyes.
For the warm-up, we calculate a rather ordinary definite integral, which was borrowed from the mathematical analysis problem book. I prefer to use the most simple interface (Classic Worksheet), in it commands are entered in symbolic form, and there is no special interface for entering formulas. We get carefully drawn integral.

We could just use the

They suggest replacing variables to get rid of the square in the denominator. So do. The integral began to look much nicer.

Now we will try to do without hints. The brain is already a little "pumped" during the comprehension of the previous step. Let's make another replacement.

The integral of the constant - what could be simpler? Here it is enough to apply one simple rule (the full list of rules is, of course, available in manuals). And simplify.
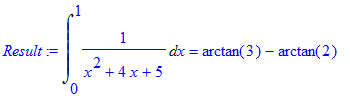
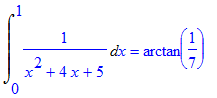
Now let's try to deal with the double improper integral, without any prompts at all.
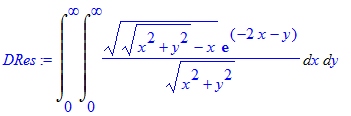
The substitution of variables is obvious. The

We simplify the integrand (
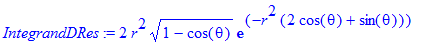
We get rid of both integrals in turn, not forgetting the boundaries. The


The answer is pleasing to the eye. If you are not happy, you can present it in the form of a fraction with a given accuracy.

I have affected only a small part of the possibilities that symbolic calculations provide. But even owning a small set of commands and correctly combining them, you can solve many interesting examples and practice your knowledge of mathematical rules and laws. In my opinion, preferences in choosing a software package do not play a decisive role, because, syntactically, all systems are quite similar to each other.
But with the literature on computer algebra systems, things are bad. This also applies to Maple: most books have been written for a long time and do not correspond to the capabilities of the new software versions. Therefore, the best that can be read to familiarize yourself with the capabilities of various packages and functions is an inexhaustible official manual .
Illustrating the above, in this post I will talk about several different scenarios for using SKA Maple in the fight against integrals. I hope that people familiar with the subtleties of symbolic calculations will find something new for themselves here. And for those to whom this way of solving problems is new, I tried to add more comments.

Scenario number 1 - "For the lazy / tired"
Anyone who is unlucky with a matan teacher, and people who just like to observe the step-by-step solution of integrals, is dedicated to a separate student package module. Some of his "chips" are good for "intricate" integrals, but more on that later.
')
So, first connect the module and limit the output of additional information. A colon at the end means that the command output will be hidden from the user's eyes.
> with(student): > infolevel[Student[Calculus1]] := 1: For the warm-up, we calculate a rather ordinary definite integral, which was borrowed from the mathematical analysis problem book. I prefer to use the most simple interface (Classic Worksheet), in it commands are entered in symbolic form, and there is no special interface for entering formulas. We get carefully drawn integral.
> Res:=Int(1/(x^2+4*x+5),x=0..1); 
We could just use the
value(Res) command, and get the result right away. But not for nothing that the student package is called that way! We are going to integrate step by step. First we need a hint. > Hint(Res); 
They suggest replacing variables to get rid of the square in the denominator. So do. The integral began to look much nicer.
> Res:=Rule[change, u = x+2, u](Res); 
Now we will try to do without hints. The brain is already a little "pumped" during the comprehension of the previous step. Let's make another replacement.
> Res:=Rule[change, u = tan(v), v](Res); 
The integral of the constant - what could be simpler? Here it is enough to apply one simple rule (the full list of rules is, of course, available in manuals). And simplify.
> Result:=Rule[constant](Res); > simplify(Result); 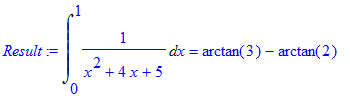
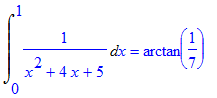
Scenario number 2 - "For enthusiasts"
Now let's try to deal with the double improper integral, without any prompts at all.
> DRes:=Doubleint(sqrt(sqrt(x^2+y^2)-x)/sqrt(x^2+y^2)*exp(-2*xy),x=0..infinity,y=0..infinity); 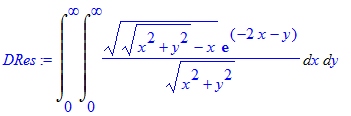
The substitution of variables is obvious. The
changevar command does an excellent job with changevar . In order to specify the conditions and get rid of the modules, add assuming . > DRes:=changevar({x=r^2*cos(theta),y=r^2*sin(theta)},DRes,[theta,r]) assuming r>0; 
We simplify the integrand (
integrand ) with the help of the cherished simplify command (it is good for simplifying expressions — and not just inside integrals). > IntegrandDRes:=simplify(integrand(DRes)) assuming r>0; 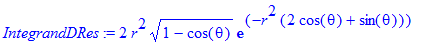
We get rid of both integrals in turn, not forgetting the boundaries. The
int command is a simple attempt to integrate an expression. It is also available outside the student package. Res:= int(IntegrandDRes,r=0..infinity) assuming (theta>0,theta<Pi/2); DRes:= int(Res,theta=0..Pi/2); 

The answer is pleasing to the eye. If you are not happy, you can present it in the form of a fraction with a given accuracy.
> evalf[16](DRes); 
Conclusion
I have affected only a small part of the possibilities that symbolic calculations provide. But even owning a small set of commands and correctly combining them, you can solve many interesting examples and practice your knowledge of mathematical rules and laws. In my opinion, preferences in choosing a software package do not play a decisive role, because, syntactically, all systems are quite similar to each other.
But with the literature on computer algebra systems, things are bad. This also applies to Maple: most books have been written for a long time and do not correspond to the capabilities of the new software versions. Therefore, the best that can be read to familiarize yourself with the capabilities of various packages and functions is an inexhaustible official manual .
Source: https://habr.com/ru/post/202338/
All Articles