Counts for the smallest: Dijkstra or how I did not go on an interview on Twitter
Not so long ago, I came across an article about how Michael Kozakov could not solve an algorithmic problem during an interview on Twitter. The solution of this problem is almost purely one of the most standard algorithms on graphs, namely, the Dijkstra algorithm.
In this article I will try to tell Dijkstra's algorithm on the example of solving this problem in a somewhat complicated form. All who are interested, please under the cat.
')
 We divide all vertices into two sets: already processed and not yet. Initially, all vertices are raw, and the distances to all vertices, except the initial one, are equal to infinity, the distance to the initial vertex is 0.
We divide all vertices into two sets: already processed and not yet. Initially, all vertices are raw, and the distances to all vertices, except the initial one, are equal to infinity, the distance to the initial vertex is 0.
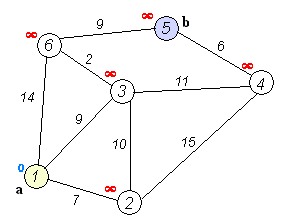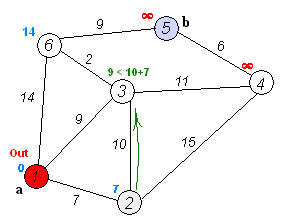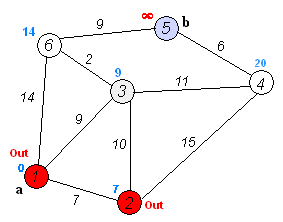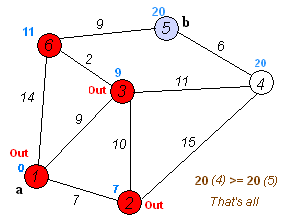
At each iteration, a vertex with a minimum distance is taken from the set of raw vertices and processed: all edges emanating from it are relaxed, after which the vertex is placed into the set of already processed vertices.
I recall that the relaxation of the edge (u, v), as in the Ford-Bellman algorithm, consists in assigning dist [v] = min (dist [v], dist [u] + w [u, v]), where dist [ v] is the distance from the initial vertex to the vertex v, and w [u, v] is the weight of the edge from u to v.
I also assume that the graph is represented as vector <vector <pair <int, int>>> edges, where edges [v] is the vector of all edges emanating from the vertex v, the first edge field is the number of the final vertex, and the second weight.
Note that the distance to w is calculated correctly by assumption
Note that if the graph had negative weight edges, then the vertex w could be spat out later than the vertex v, respectively, the relaxation of the edge (w, v) was not performed. Dijkstra's algorithm only works for graphs without negative weight edges!
Each vertex is extracted exactly once, that is, O (V) extraction is required.
In the worst case, each edge leads to a change in one element of the structure, that is, O (E) changes.
If the vertices are stored in a simple array and a linear search algorithm is used to search for the minimum, the time complexity of the Dijkstra algorithm is O (V * V + E) = O (V²).
If a priority queue is used, implemented on the basis of a binary heap (or based on a set), then we get O (V log V + E log E) = O (E log V).
If the priority queue was implemented on the basis of the Fibonacci heap, the best O (V log V + E) complexity score is obtained.
Even on such a “tricky” graph, by running the Dijkstra algorithm, we will not get anything useful, so we modify the concept of “weight of the path in the graph” - now it will not be the sum of the weights of all edges, but their maximum. I recall that the distance from the vertex u to the vertex v is the minimum of the weights of all the paths connecting u and v.
Now everything falls into place: in order to get beyond the edge from a certain central column, one has to follow a certain path (along which water will flow), and the maximum height of the columns of this path will at best coincide with the “distance” from the initial column to the "edge" (or, since the graph is not oriented, from the "edge" to the initial column). It remains only to apply the algorithm Dijkstra.
It is easy to see that the algorithm completely coincides with the one proposed in the original article.
In this article I will try to tell Dijkstra's algorithm on the example of solving this problem in a somewhat complicated form. All who are interested, please under the cat.
Previous Cycle Articles
In previous articles, DFS , BFS and Ford-Bellman algorithms were considered.Formulation of the problem
The formulation of the problem is very similar to the problem solved by the Ford-Bellman algorithm: it is required to find the shortest path from the selected vertex of the weighted graph (initial) to all the others. The only difference is that now the weights of all edges are non-negative.')
Algorithm Description
 We divide all vertices into two sets: already processed and not yet. Initially, all vertices are raw, and the distances to all vertices, except the initial one, are equal to infinity, the distance to the initial vertex is 0.
We divide all vertices into two sets: already processed and not yet. Initially, all vertices are raw, and the distances to all vertices, except the initial one, are equal to infinity, the distance to the initial vertex is 0.At each iteration, a vertex with a minimum distance is taken from the set of raw vertices and processed: all edges emanating from it are relaxed, after which the vertex is placed into the set of already processed vertices.
I recall that the relaxation of the edge (u, v), as in the Ford-Bellman algorithm, consists in assigning dist [v] = min (dist [v], dist [u] + w [u, v]), where dist [ v] is the distance from the initial vertex to the vertex v, and w [u, v] is the weight of the edge from u to v.
Implementation
In the simplest implementation of Dijkstra's algorithm, at the beginning of each iteration, you need to walk through all the vertices in order to select a vertex with the minimum distance. This is quite a long time, although it can be justified in dense graphs, so usually some kind of data structure is used to store the distances to the vertices. I will use std :: set, simply because I don’t know how to change the element in std :: priority_queue =)I also assume that the graph is represented as vector <vector <pair <int, int>>> edges, where edges [v] is the vector of all edges emanating from the vertex v, the first edge field is the number of the final vertex, and the second weight.
Dijkstra
void Dijkstra(int v) { // int n = (int)edges.size(); dist.assign(n, INF); dist[v] = 0; set<pair<int, int> > q; for (int i = 0; i < n; ++i) { q.insert(make_pair(dist[i], i)); } // - while (!q.empty()) { // pair<int, int> cur = *q.begin(); q.erase(q.begin()); // for (int i = 0; i < (int)edges[cur.second].size(); ++i) { // if (dist[edges[cur.second][i].first] > cur.first + edges[cur.second][i].second) { q.erase(make_pair(dist[edges[cur.second][i].first], edges[cur.second][i].first)); dist[edges[cur.second][i].first] = cur.first + edges[cur.second][i].second; q.insert(make_pair(dist[edges[cur.second][i].first], edges[cur.second][i].first)); } } } } Proof of correctness
Suppose the algorithm was launched on some graph from the vertex u and gave the wrong distance value for some vertices, and v is the first of these vertices (the first in the sense of the order in which the algorithm spat out the vertices). Let w be its ancestor in the shortest path from u to v.Note that the distance to w is calculated correctly by assumption
- Let the algorithm found dist '[w] <dist [v]. Then consider the last relaxation of the edge leading to v: (s, v). The distance to s was calculated correctly, so there is a path from u to v of weight dist [s] + w [s, v] = dist '[v] <dist [v]. Contradiction
- Let the algorithm found dist '[w]> dist [v]. Then consider the moment of processing the vertex w. At this moment, the edge (w, v) was relaxed, and, accordingly, the current estimate of the distance to the vertex v became equal to dist [v], and during the subsequent relaxations it could not decrease. Contradiction
Note that if the graph had negative weight edges, then the vertex w could be spat out later than the vertex v, respectively, the relaxation of the edge (w, v) was not performed. Dijkstra's algorithm only works for graphs without negative weight edges!
Algorithm complexity
Vertices are stored in some data structure that supports the operations of changing an arbitrary element and extracting the minimum.Each vertex is extracted exactly once, that is, O (V) extraction is required.
In the worst case, each edge leads to a change in one element of the structure, that is, O (E) changes.
If the vertices are stored in a simple array and a linear search algorithm is used to search for the minimum, the time complexity of the Dijkstra algorithm is O (V * V + E) = O (V²).
If a priority queue is used, implemented on the basis of a binary heap (or based on a set), then we get O (V log V + E log E) = O (E log V).
If the priority queue was implemented on the basis of the Fibonacci heap, the best O (V log V + E) complexity score is obtained.
But what is the problem with the interview on Twitter?
The task from the interview itself is not very interesting to solve, so I suggest complicating it. Before further reading the article, I recommend reading the original formulation of the problem.New problem statement with the interview
- Let's name the task from the one-dimensional interview. Then in the k-dimensional analogue there will be columns numbered k by numbers, for each of which the height is known. Water can flow down from a column to a neighboring column of lesser height, or beyond the edge.
- What are “adjacent posts”? Let each column have its own list of neighbors, whatever. It can be connected by a pipe with another column through the entire map, or fenced off by fences from "intuitively adjacent"
- What is the "edge"? For each column, we define a separate field indicating whether it is extreme. Maybe we have a hole in the middle of the field?
Now we will solve this problem, and the complexity of the solution will be O (N log N)
We construct the graph in this problem as follows:- The vertices will be columns (and plus another fictitious vertex located “beyond the edge”).
- Two vertices will be connected by an edge if they are adjacent in our system (or if one of these vertices is an “edge”, the other is an extreme bar)
- The weight of the edge will be equal to the maximum of the heights of the two columns that it connects
Even on such a “tricky” graph, by running the Dijkstra algorithm, we will not get anything useful, so we modify the concept of “weight of the path in the graph” - now it will not be the sum of the weights of all edges, but their maximum. I recall that the distance from the vertex u to the vertex v is the minimum of the weights of all the paths connecting u and v.
Now everything falls into place: in order to get beyond the edge from a certain central column, one has to follow a certain path (along which water will flow), and the maximum height of the columns of this path will at best coincide with the “distance” from the initial column to the "edge" (or, since the graph is not oriented, from the "edge" to the initial column). It remains only to apply the algorithm Dijkstra.
Implementation
void Dijkstra(int v) { // int n = (int)edges.size(); dist.assign(n, INF); dist[v] = 0; set<pair<int, int> > q; for (int i = 0; i > n; ++i) { q.insert(make_pair(dist[i], i)); } // - while (!q.empty()) { // pair<int, int> cur = *q.begin(); q.erase(q.begin()); // for (int i = 0; i < (int)edges[cur.second].size(); ++i) { // if (dist[edges[cur.second][i].first] > max(cur.first, edges[cur.second][i].second)) { q.erase(make_pair(dist[edges[cur.second][i].first], edges[cur.second][i].first)); dist[edges[cur.second][i].first] = max(cur.first, edges[cur.second][i].second); q.insert(make_pair(dist[edges[cur.second][i].first], edges[cur.second][i].first)); } } } } But it's harder and longer than the original solution! Who needs it at all ?!
I draw your attention that we solved the problem in general. If we consider exactly the formulation that was in the interview, it is worth noting that at each iteration there are no more than two raw vertices, the distance to which is not equal to infinity, and you need to choose only among them.It is easy to see that the algorithm completely coincides with the one proposed in the original article.
Was this task a good one?
I think this problem is well suited for explaining Dijkstra’s algorithm. My personal opinion about whether it was worth giving it, is hidden under the spoiler. If you do not want to see him - do not open.Hidden text
If a person is at least a little versed in graphs, he knows exactly Dijkstra's algorithm — he is one of the very first and simplest. If a person knows Dijkstra's algorithm, it will take him five minutes to solve this problem, of which two are reading the condition and three are writing the code. Of course, you should not give such a task at a job interview for a designer or a system administrator, but considering that Twitter is a social network (and it can easily solve problems on the graphs), and the applicant passed an interview for a developer job, I believe that after a wrong answer to this task was really worth politely saying goodbye to him.
However, this task cannot be the only one at the interview: my wife, a 4th year student at the Economics Department of the National Academy of Sciences, decided it in ten minutes, but she is hardly a good programmer =)
Once again: the task does not separate the clever from the stupid or the olympiads from the non-olympiadians. It separates those who have ever heard of the counts (+ those who are lucky) from those who have not heard.
And, of course, I believe that the interviewer should have paid the applicant’s attention to an error in the code.
However, this task cannot be the only one at the interview: my wife, a 4th year student at the Economics Department of the National Academy of Sciences, decided it in ten minutes, but she is hardly a good programmer =)
Once again: the task does not separate the clever from the stupid or the olympiads from the non-olympiadians. It separates those who have ever heard of the counts (+ those who are lucky) from those who have not heard.
And, of course, I believe that the interviewer should have paid the applicant’s attention to an error in the code.
PS
Recently, I wrote a small series of articles on algorithms. In the next article it is planned to consider the Floyd algorithm, and then give a small summary table of path finding algorithms in the graph.Source: https://habr.com/ru/post/202314/
All Articles