Search for solutions in logic games on the example of Gomoku

Introduction

In general, we are not talking about the classical Gomoku , but about the Russian variation “five in a row”. You have a piece of paper in the box. The rules of the game are the same as in the tic-tac-toe. The only difference is that it is necessary to build a line of 5 elements.



For such a simple game, we listened to more than one lecture. It always annoyed me that my brilliant strategy was being broken about my own carelessness. Do not worry, I thought, I'll write a program that will not make mistakes, then I'll show them all! Just spit! A couple of cycles, however, it is necessary to tinker with the user interface, but for a couple of evenings I will manage. 10 years have passed since the graduation from the institute, and I have not written the program yet.

')

Brute force

The idea is that we have no evaluation function, no heuristics. We simply arrange the elements on the field until we reach five in line. Immediately it becomes clear that this method is not suitable. Each turn generates an average of 80 new positions. By 6 moves, the number of options increases to 80 ^ 6 = 2 ^ 37 options, which is too much.

Alpha beta cut

Alpha-beta pruning is what usually limits the course of game theory at the institute. Applies ... honestly difficult to come up with a game in which it can be applied. The idea is to use the valuation function as a value criterion. The problem is that we are only interested in winning or losing. And we are completely satisfied with the victory for the greater number of steps. From here comes an important feature: in order to prove victory from a certain position, it is enough to find one move, and in order to prove defeat, it is necessary to go through all possible moves .

Solution from the end

The idea is to recognize patterns that lead to victory. Analogy with chess programs - endgame base.

This solution was implemented, but it worked slowly. So slowly that I could not debug the code. The problem is a lot of combinations. Two steps back is all that can be stored in memory.

Calculation vs. storage

After such a file, I decided not to store ready-made templates, but to find the lines in one or two moves before winning “on the fly”. Surprisingly, it worked quite well. Conclusion: it is sometimes better to decide than to store .
In order to optimize, I limited the number of possible moves to two adjacent cells around existing ones. In general, it is far from a fact that effective moves are limited to these cells, but so far my assumption is in good agreement with practice.

In depth or in width

Search in depth is preferable from the point of view of memory, but often goes too deep, although the victory is located nearby in the next branch. A wide search does not have this drawback, but requires a lot of memory to store already solved positions. Usually used forced depth search: the search goes down to a fixed depth, but for promising positions the depth increases.

Evaluation function

Search speed is very sensitive to the traversal order. To do this, they introduce a function that evaluates the “attractiveness” of moves and organizes them by the criterion of such attractiveness.


Works pretty well. The program plays at novice level. These are 2 levels of search in width and 3 levels of the forced search in depth. Unfortunately, this is completely insufficient to win always. At this point, my ideas ended, and I already thought that nothing could be improved significantly. If I had not stumbled upon the work of a certain Louis Victor Allis .

Mr. Allis and Treat-Space search

In 1992 Mr. Alice (Allis), using 10 SUN SPARC workstations, proved for the classic Gomoku with a field of 15X15 that the crosses always win. The stations had 64 and 128MB RAM, 200MB swaps. Since they used the Vrije Universiteit station in Amsterdam, their processes started only at night. The processes that did not finish during the night were killed in the morning. All it took was 1000 CPU / hours and a week of time.



Unfortunately, how to check the chains for the possibility of a counterattack, I did not understand the author. So I had to sculpt my decision on my knee. At the moment, this is the slowest and dirtiest place in the calculation.

Zero stroke heuristics

Best described here .
The idea comes down to the fact that you miss your turn, allowing the opponent to make a move. If your position is still strong, then this state is probably not the one the enemy will allow you to hit. This saves one turn in depth when analyzing.

Unfortunately, I have not figured out how to safely and effectively use it, so I don’t use it yet.

Crosses win and decision tree

With the Treat-Space search heuristics, the program plays quite strongly, but it still loses to a strong player. This is because the program is able to “see” 4 to 16 moves ahead. Sometimes, especially at the beginning of the game, it is more profitable to set moves for the future, rather than try to develop a local advantage. A person uses his experience to see directions that will give an advantage in the long term.
So we approach another problem of computer programs - lack of experience . To compensate for this, a base of openings is used in chess programs. You can do this kind of game "Five in a row." The problem is that I did not master the Homoku theory that the theory for this game is not as well developed as for chess.

Therefore, there is a natural desire to go over the decision tree entirely to find the best moves. As a bonus, you can get proof that the crosses win, and the optimal sequence as a bonus. Actually, this is what Professor Alice did in his research.


The longest chain in a perfect game for gomoku without restrictions


The longest chain in the perfect game for gomoku with restrictions

According to the theory, the 19X19 field gives the crosses a greater advantage than 15X15, so everything should be even easier for an unlimited field.

Distributed computing on the knee

Immediately it becomes clear that on one machine this does not count. On the other hand, the task is very well parallel.


The calculation lasted about a month. Unfortunately, the miracle did not happen. The number of options grew steadily. The calculation had to stop. Even on states with 17-35 moves, the decision tree is also steadily expanding.
The reason for this lies in the search in width. We started searching in width to find non-obvious solutions.



To do this, you have to bypass all the options, even the most idiotic.

Algorithm of an ant colony

My ideas ended, and I abandoned the project for almost a year, until my colleague suggested that I use the ant colony algorithm .
The idea is that we randomly choose the path that we will explore from a certain state. The probability of a move depends on the ratio of the number of victories / losses of all descendants of a given branch.
It works pretty well. The only problem is that we are not interested in how likely the opponent is losing, if there is at least one position in which he can win.

Ask your neighbor about winning

Honestly, I do not know the name of this heuristic. It is based on the fact that for many cases the opponent’s response moves can not significantly affect the gain.


We are making a “promising” move by zero. Soon we find that it leads to defeat in 17 moves.


We make the next “promising” move by zero from the same state. We find that the crosses win again, and with the same move

For different moves by zero, we have the same reciprocal move with a cross. You can simply increase the weight of the already known winning moves to reduce the number of moves being sorted.
This heuristic, combined with the ant colony algorithm, gives a huge performance boost. It is so effective that for the day of work it finds resolved positions starting from the fourth move.

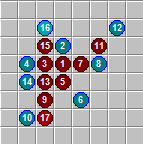
Base debuts and man

If we want to prove that the crosses start and win, it is enough for us to make one perfect move with a cross, for each possible move with a zero. This is equivalent to halving the overall search depth. In some cases, as in the picture above, the ideal moves are obvious to a person.
I plan to add the ability to selectively force the computation of certain branches in the hope that this will give me a significant increase in performance.

And let's rewrite the assembler

In none of the projects I tried to make so many optimizations and did not experience so much disappointment.
The facts are inexorable: the constant has no meaning compared to the overall complexity of the algorithm. Let me remind you that each position gives an average of 80 new positions. To go one step further, we must increase the speed of the program by 80 times !!!

So, a selective list of what I have undertaken:

• Incremental search for effective empty cells. When deepening the search, only empty cells are added around the last turn. To do this, I had to enter the state of the field in depth and quite a lot of code to support them.
• Where possible, I have made arrays of the type std :: vector <> static, in order to avoid permanent memory allocation for such arrays.
• To avoid constant allocation of memory for tree nodes, reference counts for shared_ptr nodes and fields within the structures that implement these nodes, I implemented a pool of nodes. In order not to break anything, this pool of nodes had to be used very carefully. No increase in performance was found at all, and with great joy I was able to mow down this code.

By incredible tricks and complication of the code I managed to increase the speed by 2.5 times. Feel the difference between acceleration 2.5 times and 80 times?
Often offer to do the calculation on the video card using CUDA. The problem is that GPUs are built on SIMD architecture, and they really don’t like branching, and branching is, in fact, a way of working on a tree. The only thing for which they can be applied is the search for threatening lines from one or several positions at the same time. The practical effect of this is still dubious.

Although algorithmic optimization itself has not yet been exhausted. And it is quite possible that one modern smartphone is enough for the task of such complexity.
So the algorithms rule!

Thanks

I am grateful to Dr. Louis Victor Allis for his ability to solve unsolvable problems.
I am immensely grateful to all those people from the RSDN community who helped and continue to help me cheat on this task using my resources.
I am grateful to Rustam for the idea of ​​an ant colony algorithm.
I am grateful to Vanya for the stylistic and spelling correction of the article. I hope I did not miss anything from your edits.

References and literature

Computer Chess Programming Theory
Knuth DE, Moore RW An Analysis of Alpha-Beta Priming
Allis, LV (1994). Ph.D. Thesis, University of Limburg, Maastricht.
Allis, LV, Herik, HJ van den, and Huntjens, MPH Go-Moku and Threat-Space Search
GORKOFF About AI in intellectual games
Latobco Some ideas for writing artificial intelligence for chess
Project source code
Project website