Normal numbers. Episode II: De Bruin's Attack
Good afternoon, dear habrazhiteli. As some of you may remember, in the previous post I threatened to show how a normal number is constructed, the proof of which is normal, by elementary means. Unfortunately, I have not had the opportunity to write this post for a month due to the unexpected transition of my account to read-on mode. However, now I am back, so to speak, rested and can proceed to fulfill the promise.
If you know what normal numbers are, and you wonder how to build them - please come in under cat. If you do not know what normal numbers are - read the previous article (link above), then please come in under cat. If you are not interested in how to build a normal number - still please come under the cut, because there I will talk about de Bruin's cycles, which are very interesting things in themselves.

')
Comrade de Bruin (aka de Broyne, de Bruin, and even de Bruin sometimes) is, of course, not Gauss and not Euler, but personalia is also quite significant. Among me, he is best known for results in the field of combinatorics and graph theory, however, they say, he was engaged in something else. However, in this article, its achievements in other areas can be cynically neglected.
The de Bruin cycle for some natural parameters n and k is a cyclic sequence of k n digits of a k-ary number system in which (sequences) any possible subsequence of length n occurs exactly once.
Consider examples of de Bruin cycles for different k and n.
n = 1, k = 2: the sequence “01” will be the desired cycle, because it contains once all all possible binary sequences of length 1 (that is, a zero and one).
n = 2, k = 2: the sequence "0110" suits us. Let's check: it contains subsequences "01", "11", "10" and, thanks to cyclicity, "00". These are all possible binary sequences of length 2.
n = 3, k = 10:
In general, here, for example , there is a de Bruin online cycle generator for any not too large parameters.
According to rumors, the use of de Bruijn cycles can shorten the time of a brute force, if the device being broken breaks n last entered characters as a PIN code. Instead of entering all k n possible codes in turn (which gives n * k n characters), you can enter a sequence of digits of a certain De Bruin cycle (which gives k n characters) with a small tail (n - 1 character to close cycle). Total time gain is approximately n times. However, I have never met with such devices, so for me it is just a rumor. If you have something to say about this, post, please, in the comments, I would be interested.
The first question that a mathematician should have after reading the above: “For any k and n, does the corresponding de Bruin cycle exist?” The first question that should arise for a programmer is: “How can I generate a de Bruin cycle for given k and n? »To answer both of these questions, we introduce a new definition.
The de Bruin graph for natural parameters k and n is a directed graph, the vertices of which correspond to all possible n-valued k-ary sequences, and the edges connect those and only those pairs of vertices for which the last n-1 digits of the first number coincide with the first n- 1 digits of the second number.
Obviously, having found a cycle in this graph of Hamiltonians (i.e., a closed path along its edges passing through each vertex exactly once), we will also find the de Bruin cycle for the same parameters k and n (hereinafter we will use the abbreviated notation B (k, n)), and vice versa. Indeed, the de Bruijn cycle is, in fact, “gluing together” all possible n-valued sequences according to their common (n-1) -valued subsequences. However, the Hamiltonian cycle in the De Bruin graph just provides such a method of "gluing".
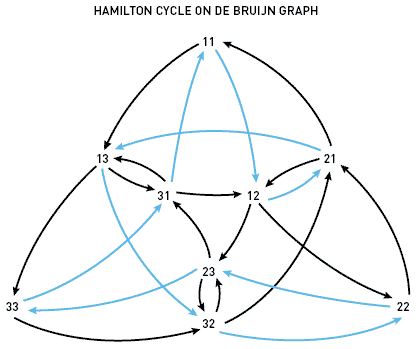
So we answered the programmer's question. If B (k, n) exists, we can find it by the corresponding algorithm on the corresponding graph. However, the mathematician is not satisfied. The existence of a Hamiltonian cycle is a completely non-obvious thing, which means it is not obvious whether B (k, n) exists . Fortunately for the mathematician, there is another remarkable property of the de Bruin graph: every Eulerian (that is, passing through all the edges) cycle corresponds to a certain de Bruyn cycle B (k, n + 1). Indeed, each edge of the de Bruin graph is a pair of “glued” n-valued sequences, which can be interpreted as a single (n + 1) -valued sequence. If one edge enters a vertex from which the second comes out, then the (n + 1) -valued sequences corresponding to these edges are “glued together” along the common n-digit sequence corresponding to this vertex.
The existence of Euler cycles is a well-studied question; The criterion for the presence of an Eulerian cycle can be found, for example, on Wikipedia :
Strong connectivity is when for any pair of vertices in a directed graph we can get from one to another, following the edges, and vice versa. The half-degree of entry is how many edges enter the top. The half degree of outcome is, accordingly, how many edges come out of it. I suggest that the reader prove independently that the de Bruin graph satisfies the condition for the existence of an Euler cycle. Seriously, if you have free time with nothing to occupy, write proof in the comments.
Still, it is not very convenient to look for de Bruin cycles using graph algorithms, and it is sinful. There are more efficient ways to build these cycles. Here I will talk about one of them: with the help of necklaces. The most inquisitive can read the original article , but I will explain everything briefly and without proof.
A necklace is a finite sequence considered up to a cyclic shift. That is, “1100”, “1001”, “0011” are different records of the same necklace. There are many interesting combinatorial results associated with necklaces, but now we will not be distracted by them.
Representative of the necklace, we will call the record that goes before all other entries in lexicographical order. The necklace from the previous example can be written in four ways: "1100", "1001", "0011", "0110". Of these, the first “alphabetically” is “0011”, which will be the representative.
By periodic reduction of a sequence, we call its smallest subsequence such that the original sequence consists of a certain number of its repetitions. For example, “0101” is “01” repeated twice, so the subsequence “01” is a periodic reduction of the sequence “0101”. Periodic reduction of the sequence "0000" will be a subsequence "0". Most of the sequences can not be represented as a repetition of some smaller "piece", so their periodic reductions coincide with themselves.
Now, having formulated these concepts, I can write an algorithm for constructing B (k, n) using necklaces:
Let's try this algorithm on the example of B (2,3). We have only four binary necklaces of length three: from all ones, from all zeros, from one one and two zeros, from one zero and two ones. Their representatives will be, respectively, "111", "000", "001", "011". Sort them alphabetically: "000", "001", "011", "111". After a periodic reduction, we get “0”, “001”, “011”, “1”. The concatenation of these four binary words - "00010111" - will be B (2,3). You can check it, you can believe my word of honor.
So, the construction of a normal number. This paragraph will be very short. Denote by B '(k, n) the sequence B (k, n), to which its first n-1 characters are added to the right. It is good because every n-digit k-ary sequence enters it exactly once, without taking into account cyclicity . To build a k-ary number, in normality of which there is no doubt, let’s take the infinite concatenation as its fractional part: B '(k, 1) + B' (k, 2) + ... + B '(k, n) + ...
In principle, this post could have been completed, but I will explain just in case. Any sequence of length m is included in B '(k, n), n ≥ m, with exactly the same frequency as any other sequence of length m. This is exactly what you need for a normal number. Accordingly, errors in frequency can occur either for n <m (and this is the initial piece of finite length, it cannot affect the asymptotic density), or at the “junctions” between de Bruin cycles.
Since the length B '(k, n) increases exponentially with increasing n, the asymptotic density of the junctions is zero, which means that the joints also cannot affect the asymptotic density of our sequence. Conclusion: in the record of the number we have constructed for every n, all sequences of length n will meet with the same asymptotic density. This is the definition of a normal number. You can shout "hurray" and throw caps into the air: the theorem is proved.
If you know what normal numbers are, and you wonder how to build them - please come in under cat. If you do not know what normal numbers are - read the previous article (link above), then please come in under cat. If you are not interested in how to build a normal number - still please come under the cut, because there I will talk about de Bruin's cycles, which are very interesting things in themselves.

')
Circus trained structures named Nicholas de Bruyna.
Comrade de Bruin (aka de Broyne, de Bruin, and even de Bruin sometimes) is, of course, not Gauss and not Euler, but personalia is also quite significant. Among me, he is best known for results in the field of combinatorics and graph theory, however, they say, he was engaged in something else. However, in this article, its achievements in other areas can be cynically neglected.
The de Bruin cycle for some natural parameters n and k is a cyclic sequence of k n digits of a k-ary number system in which (sequences) any possible subsequence of length n occurs exactly once.
Consider examples of de Bruin cycles for different k and n.
n = 1, k = 2: the sequence “01” will be the desired cycle, because it contains once all all possible binary sequences of length 1 (that is, a zero and one).
n = 2, k = 2: the sequence "0110" suits us. Let's check: it contains subsequences "01", "11", "10" and, thanks to cyclicity, "00". These are all possible binary sequences of length 2.
n = 3, k = 10:
Hidden text
0001002003004005006007008009011012013014015016017018019021022023024025026027028029031032033034035036
0370380390410420430440450460470480490510520530540550560570580590610620630640650660670680690710720730
7407507607707807908108208308408508608708808909109209309409509609709809911121131141151161171181191221
2312412512612712812913213313413513613713813914214314414514614714814915215315415515615715815916216316
4165166167168169172173174175176177178179182183184185186187188189192193194195196197198199222322422522
6227228229233234235236237238239243244245246247248249253254255256257258259263264265266267268269273274
2752762772782792832842852862872882892932942952962972982993334335336337338339344345346347348349354355
3563573583593643653663673683693743753763773783793843853863873883893943953963973983994445446447448449
4554564574584594654664674684694754764774784794854864874884894954964974984995556557558559566567568569
5765775785795865875885895965975985996667668669677678679687688689697698699777877978878979879988898999
0370380390410420430440450460470480490510520530540550560570580590610620630640650660670680690710720730
7407507607707807908108208308408508608708808909109209309409509609709809911121131141151161171181191221
2312412512612712812913213313413513613713813914214314414514614714814915215315415515615715815916216316
4165166167168169172173174175176177178179182183184185186187188189192193194195196197198199222322422522
6227228229233234235236237238239243244245246247248249253254255256257258259263264265266267268269273274
2752762772782792832842852862872882892932942952962972982993334335336337338339344345346347348349354355
3563573583593643653663673683693743753763773783793843853863873883893943953963973983994445446447448449
4554564574584594654664674684694754764774784794854864874884894954964974984995556557558559566567568569
5765775785795865875885895965975985996667668669677678679687688689697698699777877978878979879988898999
In general, here, for example , there is a de Bruin online cycle generator for any not too large parameters.
According to rumors, the use of de Bruijn cycles can shorten the time of a brute force, if the device being broken breaks n last entered characters as a PIN code. Instead of entering all k n possible codes in turn (which gives n * k n characters), you can enter a sequence of digits of a certain De Bruin cycle (which gives k n characters) with a small tail (n - 1 character to close cycle). Total time gain is approximately n times. However, I have never met with such devices, so for me it is just a rumor. If you have something to say about this, post, please, in the comments, I would be interested.
The first question that a mathematician should have after reading the above: “For any k and n, does the corresponding de Bruin cycle exist?” The first question that should arise for a programmer is: “How can I generate a de Bruin cycle for given k and n? »To answer both of these questions, we introduce a new definition.
The de Bruin graph for natural parameters k and n is a directed graph, the vertices of which correspond to all possible n-valued k-ary sequences, and the edges connect those and only those pairs of vertices for which the last n-1 digits of the first number coincide with the first n- 1 digits of the second number.
Obviously, having found a cycle in this graph of Hamiltonians (i.e., a closed path along its edges passing through each vertex exactly once), we will also find the de Bruin cycle for the same parameters k and n (hereinafter we will use the abbreviated notation B (k, n)), and vice versa. Indeed, the de Bruijn cycle is, in fact, “gluing together” all possible n-valued sequences according to their common (n-1) -valued subsequences. However, the Hamiltonian cycle in the De Bruin graph just provides such a method of "gluing".

So we answered the programmer's question. If B (k, n) exists, we can find it by the corresponding algorithm on the corresponding graph. However, the mathematician is not satisfied. The existence of a Hamiltonian cycle is a completely non-obvious thing, which means it is not obvious whether B (k, n) exists . Fortunately for the mathematician, there is another remarkable property of the de Bruin graph: every Eulerian (that is, passing through all the edges) cycle corresponds to a certain de Bruyn cycle B (k, n + 1). Indeed, each edge of the de Bruin graph is a pair of “glued” n-valued sequences, which can be interpreted as a single (n + 1) -valued sequence. If one edge enters a vertex from which the second comes out, then the (n + 1) -valued sequences corresponding to these edges are “glued together” along the common n-digit sequence corresponding to this vertex.
The existence of Euler cycles is a well-studied question; The criterion for the presence of an Eulerian cycle can be found, for example, on Wikipedia :
An oriented graph contains an Euler cycle if and only if it is strongly connected and for each vertex of the graph its half degree of entry is equal to its half degree of outcome, that is, as many edges enter the vertex as there are out of it.
Strong connectivity is when for any pair of vertices in a directed graph we can get from one to another, following the edges, and vice versa. The half-degree of entry is how many edges enter the top. The half degree of outcome is, accordingly, how many edges come out of it. I suggest that the reader prove independently that the de Bruin graph satisfies the condition for the existence of an Euler cycle. Seriously, if you have free time with nothing to occupy, write proof in the comments.
Say no to graphomania
Still, it is not very convenient to look for de Bruin cycles using graph algorithms, and it is sinful. There are more efficient ways to build these cycles. Here I will talk about one of them: with the help of necklaces. The most inquisitive can read the original article , but I will explain everything briefly and without proof.
A necklace is a finite sequence considered up to a cyclic shift. That is, “1100”, “1001”, “0011” are different records of the same necklace. There are many interesting combinatorial results associated with necklaces, but now we will not be distracted by them.
Representative of the necklace, we will call the record that goes before all other entries in lexicographical order. The necklace from the previous example can be written in four ways: "1100", "1001", "0011", "0110". Of these, the first “alphabetically” is “0011”, which will be the representative.
By periodic reduction of a sequence, we call its smallest subsequence such that the original sequence consists of a certain number of its repetitions. For example, “0101” is “01” repeated twice, so the subsequence “01” is a periodic reduction of the sequence “0101”. Periodic reduction of the sequence "0000" will be a subsequence "0". Most of the sequences can not be represented as a repetition of some smaller "piece", so their periodic reductions coincide with themselves.
Now, having formulated these concepts, I can write an algorithm for constructing B (k, n) using necklaces:
- We take all possible k-ary necklaces of length n;
- For each of them choose a representative;
- We write out the representatives in the lexicographical order;
- We replace each representative with a periodic reduction;
- ???
- We built B (k, n).
Let's try this algorithm on the example of B (2,3). We have only four binary necklaces of length three: from all ones, from all zeros, from one one and two zeros, from one zero and two ones. Their representatives will be, respectively, "111", "000", "001", "011". Sort them alphabetically: "000", "001", "011", "111". After a periodic reduction, we get “0”, “001”, “011”, “1”. The concatenation of these four binary words - "00010111" - will be B (2,3). You can check it, you can believe my word of honor.
Let's return to our sheep
So, the construction of a normal number. This paragraph will be very short. Denote by B '(k, n) the sequence B (k, n), to which its first n-1 characters are added to the right. It is good because every n-digit k-ary sequence enters it exactly once, without taking into account cyclicity . To build a k-ary number, in normality of which there is no doubt, let’s take the infinite concatenation as its fractional part: B '(k, 1) + B' (k, 2) + ... + B '(k, n) + ...
In principle, this post could have been completed, but I will explain just in case. Any sequence of length m is included in B '(k, n), n ≥ m, with exactly the same frequency as any other sequence of length m. This is exactly what you need for a normal number. Accordingly, errors in frequency can occur either for n <m (and this is the initial piece of finite length, it cannot affect the asymptotic density), or at the “junctions” between de Bruin cycles.
Since the length B '(k, n) increases exponentially with increasing n, the asymptotic density of the junctions is zero, which means that the joints also cannot affect the asymptotic density of our sequence. Conclusion: in the record of the number we have constructed for every n, all sequences of length n will meet with the same asymptotic density. This is the definition of a normal number. You can shout "hurray" and throw caps into the air: the theorem is proved.
Source: https://habr.com/ru/post/202220/
All Articles