Never repeat this house: modification of the HC-128 encryption algorithm
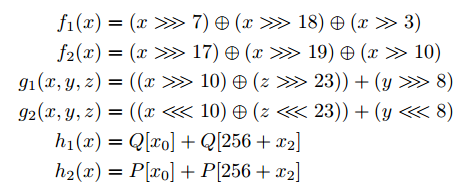
HC-128 (pdf) - finalist of the European project eSTREAM , stream cipher with a rather large internal state
(2 independent arrays of 512 32bit words). It is very smart if you encrypt large streams, but since the initialization of these arrays takes a decent amount of time, it is not very efficient in batch mode. On the right are 6 main functions that are used in it. It is not overloaded with scary long arrays of constants, its implementation (under the cut) compared to others looks simple and more or less understandable. It all started with the fact that I hooked two functions f1 and f2
Here is the standard implementation, taken from the BouncyCastle library
HC-128
package org.bouncycastle.crypto.engines; import org.bouncycastle.crypto.CipherParameters; import org.bouncycastle.crypto.DataLengthException; import org.bouncycastle.crypto.StreamCipher; import org.bouncycastle.crypto.params.KeyParameter; import org.bouncycastle.crypto.params.ParametersWithIV; /** * HC-128 is a software-efficient stream cipher created by Hongjun Wu. It * generates keystream from a 128-bit secret key and a 128-bit initialization * vector. * <p> * http://www.ecrypt.eu.org/stream/p3ciphers/hc/hc128_p3.pdf * </p><p> * It is a third phase candidate in the eStream contest, and is patent-free. * No attacks are known as of today (April 2007). See * * http://www.ecrypt.eu.org/stream/hcp3.html * </p> */ public class HC128Engine implements StreamCipher { private int[] p = new int[512]; private int[] q = new int[512]; private int cnt = 0; private static int f1(int x) { return rotateRight(x, 7) ^ rotateRight(x, 18) ^ (x >>> 3); } private static int f2(int x) { return rotateRight(x, 17) ^ rotateRight(x, 19) ^ (x >>> 10); } private int g1(int x, int y, int z) { return (rotateRight(x, 10) ^ rotateRight(z, 23)) + rotateRight(y, 8); } private int g2(int x, int y, int z) { return (rotateLeft(x, 10) ^ rotateLeft(z, 23)) + rotateLeft(y, 8); } private static int rotateLeft( int x, int bits) { return (x << bits) | (x >>> -bits); } private static int rotateRight( int x, int bits) { return (x >>> bits) | (x << -bits); } private int h1(int x) { return q[x & 0xFF] + q[((x >> 16) & 0xFF) + 256]; } private int h2(int x) { return p[x & 0xFF] + p[((x >> 16) & 0xFF) + 256]; } private static int mod1024(int x) { return x & 0x3FF; } private static int mod512(int x) { return x & 0x1FF; } private static int dim(int x, int y) { return mod512(x - y); } private int step() { int j = mod512(cnt); int ret; if (cnt < 512) { p[j] += g1(p[dim(j, 3)], p[dim(j, 10)], p[dim(j, 511)]); ret = h1(p[dim(j, 12)]) ^ p[j]; } else { q[j] += g2(q[dim(j, 3)], q[dim(j, 10)], q[dim(j, 511)]); ret = h2(q[dim(j, 12)]) ^ q[j]; } cnt = mod1024(cnt + 1); return ret; } private byte[] key, iv; private boolean initialised; private void init() { if (key.length != 16) { throw new java.lang.IllegalArgumentException( "The key must be 128 bits long"); } cnt = 0; int[] w = new int[1280]; for (int i = 0; i < 16; i++) { w[i >> 2] |= (key[i] & 0xff) << (8 * (i & 0x3)); } System.arraycopy(w, 0, w, 4, 4); for (int i = 0; i < iv.length && i < 16; i++) { w[(i >> 2) + 8] |= (iv[i] & 0xff) << (8 * (i & 0x3)); } System.arraycopy(w, 8, w, 12, 4); for (int i = 16; i < 1280; i++) { w[i] = f2(w[i - 2]) + w[i - 7] + f1(w[i - 15]) + w[i - 16] + i; } System.arraycopy(w, 256, p, 0, 512); System.arraycopy(w, 768, q, 0, 512); for (int i = 0; i < 512; i++) { p[i] = step(); } for (int i = 0; i < 512; i++) { q[i] = step(); } cnt = 0; } public String getAlgorithmName() { return "HC-128"; } /** * Initialise a HC-128 cipher. * * @param forEncryption whether or not we are for encryption. Irrelevant, as * encryption and decryption are the same. * @param params the parameters required to set up the cipher. * @throws IllegalArgumentException if the params argument is * inappropriate (ie. the key is not 128 bit long). */ public void init(boolean forEncryption, CipherParameters params) throws IllegalArgumentException { CipherParameters keyParam = params; if (params instanceof ParametersWithIV) { iv = ((ParametersWithIV)params).getIV(); keyParam = ((ParametersWithIV)params).getParameters(); } else { iv = new byte[0]; } if (keyParam instanceof KeyParameter) { key = ((KeyParameter)keyParam).getKey(); init(); } else { throw new IllegalArgumentException( "Invalid parameter passed to HC128 init - " + params.getClass().getName()); } initialised = true; } private byte[] buf = new byte[4]; private int idx = 0; private byte getByte() { if (idx == 0) { int step = step(); buf[0] = (byte)(step & 0xFF); step >>= 8; buf[1] = (byte)(step & 0xFF); step >>= 8; buf[2] = (byte)(step & 0xFF); step >>= 8; buf[3] = (byte)(step & 0xFF); } byte ret = buf[idx]; idx = idx + 1 & 0x3; return ret; } public void processBytes(byte[] in, int inOff, int len, byte[] out, int outOff) throws DataLengthException { if (!initialised) { throw new IllegalStateException(getAlgorithmName() + " not initialised"); } if ((inOff + len) > in.length) { throw new DataLengthException("input buffer too short"); } if ((outOff + len) > out.length) { throw new DataLengthException("output buffer too short"); } for (int i = 0; i < len; i++) { out[outOff + i] = (byte)(in[inOff + i] ^ getByte()); } } public void reset() { idx = 0; init(); } public byte returnByte(byte in) { return (byte)(in ^ getByte()); } } ')
About the functions f1 and f2 I wrote earlier. In short, they are taken from SHA-2 (hello, NSA!) And represent a unique transformation of one 32-bit number to another.
I was interested in constants in these functions, where they were taken from and how they were calculated. It turned out that there is a little more than 0 information, all that is given in the link above. I counted the period of these two functions, it was not the maximum of all, and I picked up constants that corresponded to the maximum period. A simple cycle, searching through all three constants, searched for triples, which will have a maximum period. Well, it looked that the values of two different triples did not overlap during the calculation of the period. Here, for example, such triples (there are many such pairs, I chose those that I liked).
{22, 13, 3} and {18, 4, 9} instead of the original {7, 18, 3} and {17, 19, 10}
I do not know what the NSA was guided by when developing these functions, maybe they have a bookmark, and maybe not. But it is very similar to the fact that my constants are not worse than theirs. They also provide a one-to-one correspondence (checked over all values of 0 - (2 32 -1)) and have a longer cycle than the standard ones. So, feel free to replace them with my
private static int f1(int x) { return rotateRight(x, 22) ^ rotateRight(x, 13) ^ (x >>> 3); } private static int f2(int x) { return rotateRight(x, 18) ^ rotateRight(x, 4) ^ (x >>> 9); } C figured it out.
Now one more thing. I came across a document with combinatorial analysis of HC-128. There is a billion matan, but what is more interesting - there are suggestions for improving the functions of h1 , h2 and g1 , g2 (section 4)
The essence of the improvements is the following: The functions h1 (x) and h2 (x) use only 16 bits from the 32 provided by them. These 16 bits are used as 2 indices (2x8) in the P and Q state arrays. But it is necessary to use all 32, otherwise it is possible under certain conditions to restore the internal state. Therefore, what is considered initially in these functions (the sum of two elements modulo 2 32 ) is xorim with x itself. It will look like this (compare with the option above):
private int h1(int x) { return (q[x & 0xFF] + q[((x >> 16) & 0xFF) + 256]) ^ x; } private int h2(int x) { return (p[x & 0xFF] + p[((x >> 16) & 0xFF) + 256]) ^ x; } Now about the functions g1 (x) and g2 (x) . Arrays of states P and Q live independently of each other. Therefore, under adverse conditions (recognition of one of these arrays and part of the stream of generated bytes), this can lead to bad consequences.
Therefore, we modify the functions g1 and g2 so that each element of P depends on a random element of Q and vice versa. And instead of cyclically shifting the element y, we take a few bits from it as an index for an element from the arrays Q and P.
private int g1(int x, int y, int z) { return (rotateRight(x, 10) ^ rotateRight(z, 23)) + Q[(y >> 7) & 0x1FF]; } private int g2(int x, int y, int z) { return (rotateLeft(x, 10) ^ rotateLeft(z, 23)) + P[(y >> 7) & 0x1FF]; } That's all, now we have a new algorithm, not inferior (and, in theory, superior) to the original in-line HC-128.
Comment
Of course, this is all by and large the game and I just have to advise you not to use such things in real applications . But as a charge for the brain, for self-application and deliberately avoiding standards and patents (if HC-128 were patented), such studies and careful modifications may well have the right to life. For example, I use this option in the procedure of slowing down a password hash (I form a hash (password) + hash (hash (password)) + (hash (password) + hash (hash (password)) from the password of a 15-kilobyte array) and so on ... ), I initialize the modified HC-128 hash from this array, and then in a cycle several million times I encrypt different small sections of this array with the modified HC-128 in order to finally calculate the hash from the array, which will be a slow hash from the password.
By the way, something like Sponge function. But this is me after doper.
After this cycle, I once again consider the hash of the array, this will be a slow password hash. An effective brutal-force to such horror will be simply impossible to write.
Here is the class that does it. ObfuscatorEngine is a modified HC-128. entropy is an array that is collected from hashes and then encrypted in chunks in random places.
The number of iterations is a prime number. It is also interesting to look at the place where offset is calculated.
SlowHasher
package com.paranoim.crypto.utils; import java.util.Arrays; import org.bouncycastle.crypto.util.Pack; import com.paranoim.crypto.Consts; import com.paranoim.crypto.digest.SHA3_256; import com.paranoim.crypto.digest.SHA3_512; import com.paranoim.crypto.utils.obfuscator.ObfuscatorEngine; import fr.cryptohash.DigestEngine; import fr.cryptohash.Keccak256; import fr.cryptohash.Keccak512; /** * @author scratch * * @description this class does calculation of hash of a password but with many iterations, * so that it would be difficult to find with brute force * * @created 06.08.2010 */ public class SlowHasher { private static final int ITERATIONS_COUNT = 0x133ECD; private static final int CHUNK_SIZE = 71; public static byte[] calculateSlowHash(final String password, final byte[] salt) { if (salt.length != Consts.BIG_SALT_SIZE) { throw new IllegalArgumentException("Salt size must be " + Consts.BIG_SALT_SIZE + " bytes!"); } final byte[] saltedPassword = ByteUtils.concat(salt, password.getBytes()); final byte[] hashOfSaltedPassword = SHA3_512.process(saltedPassword); // hash of (salt+password) final ObfuscatorEngine engine = new ObfuscatorEngine(); // used to mix bytes //compute initial entropy string final byte[] entropy = getInitialEntropy(engine, hashOfSaltedPassword, saltedPassword); final byte[] entropyHash = SHA3_512.process(entropy); engine.init(entropyHash); // 16 bytes used as key, 16 as iv final int maxOffset = entropy.length - CHUNK_SIZE + 1; int offset = (Pack.bigEndianToInt(entropyHash, 7) & 0x7FFFFFFF) % maxOffset; // main loop for (int i = 0; i < ITERATIONS_COUNT; i++) { engine.processBytes(entropy, offset = (Pack.bigEndianToInt(entropy, offset) & 0x7FFFFFFF) % maxOffset, CHUNK_SIZE, entropy, offset); } //finalization process engine.init(SHA3_256.process(entropy)); engine.processBytes(entropy, 0, entropy.length, entropy, 0); engine.processBytes(entropyHash, 0, entropyHash.length, entropyHash, 0); return SHA3_256.process(ByteUtils.concat(entropyHash, entropy)); } private static byte[] getInitialEntropy(final ObfuscatorEngine engine, final byte[] hashOfSaltedPassword, final byte[] saltedPassword) { //final ExtendedDigest sha256 = new SHA3Digest(256); //final ExtendedDigest sha512 = new SHA3Digest(512); final DigestEngine sha256 = new Keccak256(); final DigestEngine sha512 = new Keccak512(); final byte[] hash32 = new byte[32]; final byte[] hash64 = new byte[64]; final byte[] sp = Arrays.copyOf(saltedPassword, saltedPassword.length); final byte[] h = Arrays.copyOf(hashOfSaltedPassword, hashOfSaltedPassword.length); byte[] entropy = ByteUtils.concat(h, sp); engine.init(hashOfSaltedPassword); engine.processBytes(entropy, 0, entropy.length, entropy, 0); for (int i = 0; i < hashOfSaltedPassword.length << 1; i++) // 128 iterations { final byte b = hashOfSaltedPassword[i >> 1]; // i/2 if (((b >> (i & 1)) & 1) == 1) // we check 1st bit of b on even i and 2nd on odd { engine.processBytes(sp, 0, sp.length, sp, 0); entropy = ByteUtils.concat(sp, entropy); hash(sha512, entropy, hash64); entropy = ByteUtils.concat(entropy, hash64); hash(sha256, entropy, hash32); engine.init(hash32); engine.processBytes(entropy, 0, entropy.length, entropy, 0); } else { engine.processBytes(h, 0, h.length, h, 0); entropy = ByteUtils.concat(entropy, h); hash(sha512, entropy, hash64); entropy = ByteUtils.concat(hash64, entropy); hash(sha256, entropy, hash32); engine.init(hash32); engine.processBytes(entropy, 0, entropy.length, entropy, 0); } } return entropy; } private static void hash(final DigestEngine digest, final byte[] data, final byte[] result) { digest.update(data, 0, data.length); digest.digest(result, 0, result.length); } } Here is such a Friday etude.
Source: https://habr.com/ru/post/202210/
All Articles