Geekly Articles each Day
📜 ⬆️ ⬇️

Implicit predicates

Here we will talk about some aspects of computer security related to the entanglement of the program code. That was what I was interested in in connection with the development of the .NET application obfuscator - a program to protect the .NET code from hacking. There is another - the dark side: the developers of viruses and other bad things are very interested in code obfuscation, but they are not interesting for us.


Emulators


So, you have come up with a super algorithm for tangling the program code. When decompiling, the code looks simply out of order and no one will analyze it exactly. It seemed: victory! But no. Naturally, nobody will analyze the obfuscated code ... by hand. The hacker will understand how you tangled the code and write "unraveling". If your algorithm was strong enough, then the hacker will have to write his own emulator, but this is not such a problem as it may seem at first glance - there are available emulators on the network and even specially written for hacking purposes.

From the theory of computer science it is known that there is no and there will never be an algorithm that determines whether a program will stop or work forever - the so-called “stop problem”. This ensures that a hacker emulator, unraveling an obfuscated program, will do it as if “locally”: it will not be able to find out the state and value of all variables involved in each code segment and therefore at the points of conditional branching it will often be assumed that all possible variations programs. It is here that a solution comes to mind: a tangled code will be filled with transitions to conditions that will always be true, but it will be difficult to emulate and understand. Like this:
') 
if ((x+x & 1) == 0) good_code else


“But this is just one of those tangles that a hacker is going to bypass with an emulator,” you will say, and you will be right. And what if you come up with a thousand such tricks? Oh, this is a solution if you have a legion of programmers, each of whom comes up with tricks not similar to the tricks of others. In reality, this is not the case. In reality, you think a week and come up with thirty tricks, and the hacker looks at the code one day and finds all thirty tricks, because thirty is not so much.


In the domain associated with code obfuscation, identically true conditional expressions are called “implicit predicates” (the original term “opaque predicates”). Further I will use the words “predicate” and “condition” as synonyms. This topic was invented a long time ago and I honestly do not know who the original author is, there must be folklore. Several prominent predicate articles:



Ideal generator of implicit predicates


We formulate what a perfect super implicit predicate generator should look like. It creates predicates P (x1, x2, ..., xn), depending on the variables x1, x2, ..., xn, and can create both identically true and not always true predicates depending on the desire of the user of the generator. And the generator has the following fantastic characteristics:

  1. the predicate is generated in linear time from length;
  2. the predicate is very similar to the usual condition from the usual program (secrecy);
  3. there is not and cannot exist (!) an algorithm that would determine that the predicate is generated by our generator;
  4. there is not and cannot exist (!) an algorithm that, according to the generated predicate, it can always determine whether it is true or there are input parameters on which it is false;
  5. there is no probabilistic algorithm that would correctly determine, on average, in at least 80% of cases (the figure is found using a scientific method) whether the predicate created by the generator is identically true.

Now it is necessary to understand whether such a thing is theoretically possible.

Point 4 seems to be possible . Let me remind you that the Diophantine equation is an equation of the form f (x1, x2, ..., xn) = 0, where f is a polynomial with integer coefficients, and X are non-negative integer numbers. Turning again to the theory of computer science, we recall that there is not and cannot exist an algorithm that, according to any Diophantine equation, would determine whether it has a solution or not. In particular, according to Fermat's great theorem, the Diophantine equation (x + 1) * (x + 1) * (x + 1) + (y + 1) * (y + 1) * (y + 1) - (z + 1 ) * (z + 1) * (z + 1) = 0 has no solutions. It seemed: this is where to dig! But do not hurry. The Diophantine equation is not a set of sums and products of ints with values ​​from 0 to 4 billion, but a set of sums and products of integers with values ​​from 0 to infinity. You will have to write them down with the help of the so-called “long arithmetic” and they will look very strange in the code.

Point 2 bothers everyone . Intuitively secretive, we call a predicate that does not stand out in a crowd of real, "non-tacit" predicates from real programs. Smart people have already analyzed many typical applications and found that most of the predicates in them are completely uncomplicated: x == 0, x == y, x> 0, etc., where x, y are int variables (in the second of these Above the articles, smart people just in between analyze the conditions of typical java programs). No need to guess for a long time to understand that the condition of secrecy is very important for predicates. Indeed, a hacker can simply find all the “strange” predicates and somehow isolate them or even remove them altogether, which we do not need at all.

Point 4 is not possible due to point 2 ... though . So, if a predicate is arithmetic and it is “hidden”, then it is likely that only arithmetic with integers is involved in it, which means there is an algorithm that will check whether the predicate is always true: just select all the values ​​of ints included in the predicate. But this is not bad, because at best, for the analysis of the predicate, you will have to go over 4 billion values! And if there are two variables in the predicate? So we, with a clear conscience, assuming that P <NP, weaken the fourth characteristic of the generator: the task of identifying the fact that the predicate created by the generator is always true should be NP-complete. Of course, if it turns out that P = NP, then this is also hardly an option, but for now you can sleep well. Here I recall the 3-SAT - the well-known NP-complete task that God himself commanded to recall at this moment. But the predicates obtained along this path can hardly be called hidden.

Paragraphs 1, 3 and 5 are left silent - too delicate question for a short article.

Program execution graph


Arithmetic predicates are called predicates of the form f (x1, ..., xn) <g (x1, ... xn) or f (x1, ..., xn) == g (x1, ..., xn), where all X are of the int type, and f and g are ordinary arithmetic expressions. Why should the predicate necessarily be arithmetic? No, I should not and do not even say that in the text below I can convince you that I must. Nevertheless, I will cite the considerations that led me to believe that arithmetic predicates are the most real.

If you think about it, then it is clear that obfuscation with the help of implicit predicates has one main goal - to entangle the graph of program execution. The execution graph is the only piece of information that we have at the obfuscation stage and which the hacker does not have at the hacking stage. We have found above that it is indeed theoretically possible to permanently confuse this information.

Is the arithmetic predicate implicit (that is, always true)? This is an NP-complete task. What does this pointer indicate in this place of the program? This is an unsolvable problem, that is, there is no general algorithm for solving such an issue, as in the case of a stop problem. That's fine: the unsolvable is better than the NP-complete. The following idea of ​​the method of constructing implicit predicates is drawn from the second article cited above (Collberg, Clark, Low).

Let's, since we have the execution graph, we will scroll through the program invisible code that builds and modifies somewhere in memory some rather complex dynamic structure. It really may not be noticeable: who knows what it took to write to memory?
And we will know at each specific point of the program what the structure state is and what the pointers contained in it indicate.
Based on this knowledge, we stick in implicit predicates and dead code under implicit predicates, which causes some parts of the program that modify our hidden structure.
As a result, the hacker no longer possesses our knowledge of the structure, unless he solves the unsolvable problem of resolving pointers.
Consider a toy example. Let a part of the initial graph of the program execution look like:

In the obfuscated program, we form in memory a wildly complex structure consisting of one four-byte number and a pointer to this number. Let p be a pointer. Let at the entrance to the left drawn piece of the graph (* p) is guaranteed to be 1. The graph is modified as follows:

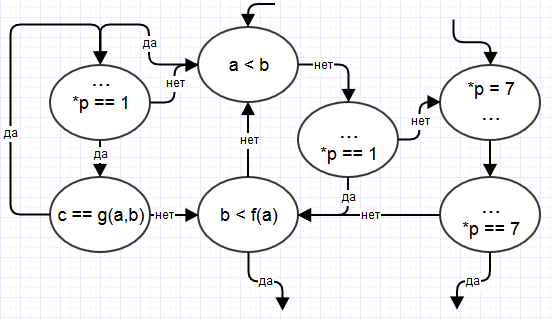
If it was previously possible to find out that * p == 1 could be difficult, then now you can additionally make an incorrect assumption on this piece, that sometimes * p == 7 and in the left part of the figure.

This is a good method and is better than arithmetic predicates. But there is one big BUT: in reality, we, like the hacker, do not know the execution graph. All this mean reflex, callbacks / delegates and other unpredictable ways to execute code. And if the code is generated in memory? Yes, this also happens, and especially in .NET. However, we know the execution graph locally. In .NET, at a minimum, you can be confident in the graph of code execution within each specific method. But if you insert the creation and construction of a certain structure in memory in each method, then it is unlikely to be secretive. This is how stealth, or rather its absence, prevents us from using this method.

There are other methods for constructing implicit predicates, but all of them (those I heard with the edge of my ear) are tied to the graph of the execution of the entire program and look cumbersome in the context of one method. Another thing is arithmetic predicates.

Implementation


In an ideal implicit predicate generator there is another big plus: the algorithm of your generator should not be secret! Our implementation of the generator, unfortunately, is not quite perfect, and we will not disclose all the details of the implementation of our algorithm. However, I did not find someone even close to the ideal generator. The topic is very interesting, and I would be happy to continue its discussion in the comments.

Below are some of the results of our implicit predicate generator. Excerpts from the beginning, middle, and end of the list of predicates (3000 pieces; priority of operations as in # ~; * /%; + -; ""; &; ^; |; all int variables):

  ~x != x (x + x & 1) == 0 (x + -x & 1) == 0 ~x != x * 4u >> 2 (-x & 1) == (x & 1) ((-x ^ x) & 1) == 0 (x * 0x80 & 0x56) == 0 (x << 1 ^ 0x1765) != 0 ~(-x * 0x40) != x << 6 (~(x * 0x80) & 0x3d) == 0x3d x - 0x9d227fa9 != x - 0x699c945e (y ^ y - 0x35f5f4d2) != 0x42a26409 (x * 0x20000000 & 0x19a27923) == 0 (int)(y * 9u + y * 0xf7u >> 3) >= 0 (x * 4 & 8) == (x + x * 3 - 0x1fef9d8f & 8) (x | 0xffffdbe8) - 0x1baa != x || (x & 0x10) == 0x10 (x ^ 0x1145f) != 0 || (x | 0xfffeffff) == 0xffffffff (uint)x / 0x59d7e3 != 0x90298cf9 || (x * 3 + x & 3) == 0 ((uint)x % 0x38 + 0xe4df62c8 & 0x6d755e00) == 0x64554200 (x ^ 0x770363c6) != 0 || ((uint)x >> 0x19 ^ 0x926797eb) != 0 (uint)y / 0x2369af8 - 0x78400000 != (uint)x / 0x1f2ce * 0x10 (x & 0x8e3ef800) != 0x70641deb && (uint)x / 0x9388ea != 0x3ab6921c


Publication author: Dmitry Kosolobov, Appfuscator developer.

Source: https://habr.com/ru/post/202162/

More articles:


All Articles