Incorrect interpretation of the Aho-Korasik algorithm
In the distant (and perhaps not very distant) of 1975, Alfred Aho and Margaret Corasic published an article in which an algorithm was described in detail for efficiently finding all occurrences of all sample lines in a given string. In the future, this algorithm was called the “Aho-Korasik algorithm”. It is not surprising that after some time technical and "artistic" translations of this article into Russian appeared. Sometimes I even met the free statements of the essence of the algorithm in the form in which the author understands it. And the latter, judging by the text, learned about the algorithm far from the original source. I don’t know if there was a translation that served as the primary source of the problem, but I’ve come across more and more articles describing the Aho-Korasik algorithm, in which the same cardinal error was made. The last straw was the article of the user rmq on Habré , which this error did not pass. Actually, I would like to tell the public about this mistake in my article.
Note: the rmq user article , as it turned out, does not contain this error. How it is solved there will tell below. And many thanks to him, if it were not for his topic, I would not have written my own and would not have received an invite!
Before the start, a couple of words about the target audience: Most likely, those who have been familiar with the Aho-Korasik algorithm for a long time will not be interested in my article, since they have long been aware of its features. At least, all my familiar programmers who have repeatedly used this algorithm know about the existence of its incorrect interpretations firsthand. But for beginners and those who did not happen to often use it in practice, this article can be quite useful.
So, let's begin.
In order not to waste the readers' time, I will miss the detailed descriptions of the algorithm (this can be read in the original article) and I will start with an example and a picture in order to quickly run through the terms and talk further "in one language".
Suppose we look for the following list of sample strings: {"HE", "SHE", "HIS", "HER"}. First we need to build an automaton. That finite automaton with states and transitions, on the basis of which the Aho-Korasik algorithm is built. The black circle denotes the initial state of the automaton. Blue circles will denote the next state of the automaton, the achievement of which does not mean the fact of detection of the sample line. And finally, blue circles with a cross-hair are another state of the automaton, the achievement of which means the fact of detection of the sample line. Naturally, transitions stretch between them - black arrows signed by letters, which are a condition for the transition. They will be called the main transitions. In the absence of a main transition for the next input symbol, the automaton switches to the initial state. Let's call them zero transitions. I do not specifically indicate these transitions in order not to clutter up the drawing. For zero transitions, it is worth noting that when you navigate through them, the input symbol is not absorbed, that is, it remains in the input line and will be used again after the transition. The exception is the zero transition from the initial state, where, in fact, the state does not change, and the input symbol is absorbed.
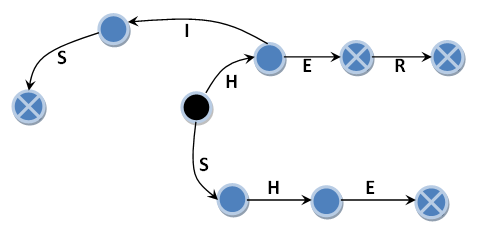
The figure shows four blue circles with a cross, each of which corresponds to one of the rows of patterns. In fact, already in this example the same error was laid. The original algorithm describes the machine a little differently. But first things first.
Recall the so-called suffix links. These are transitions that indicate which state you need to go to if there is no main transition for the next character in the input line. In the following figure, they are indicated by dotted black arrows. We will call them suffixed transitions or suffix links. The transition by suffix links by analogy with the zero transition does not absorb the input character. As in the first case, I do not depict transitions leading to the initial state in the absence of a main transition.
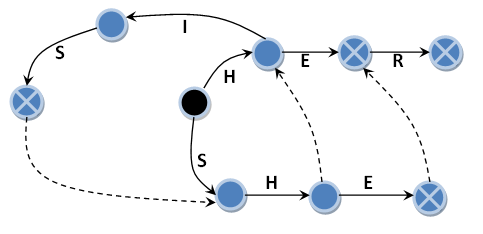
In the example without suffix links, but with zero transitions, all occurrences will be found in the string “HERHEHIS” (“HE”, “HER”, “HE”, “HIS”). But in the input line “HISHER” only three occurrences will be found (“HIS”, “HE”, “HER”) and the machine will not detect the occurrence of the sample string “SHE”, which is easy to verify. In the case of suffix links for the string “HERHEHIS”, the result will be the same, and for the string “HISHER” the result will be a list of four entries found: (“HIS”, “SHE”, “HE”, “HER”). That is, in the latter case, all occurrences were found. No, no, this is not the mistake that I wanted to talk about. In no case do not think so. To someone forgot about the suffix links, I have not seen this before. Still ahead.
I did not begin to describe in detail the algorithm for constructing an automaton, but we will consider the search algorithm for the cases described above in more detail. To do this, for the sake of convenience, we give for the beginning an automaton without suffix links, in which we enumerate its states (blue numbers next to the corresponding circles).
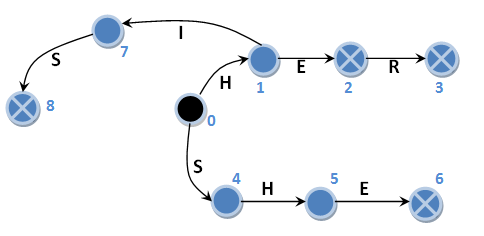
Yes, by the way, let me remind you that, despite the lack of suffix links, this machine goes into the initial state in the absence of the main direction while preserving the input symbol. In the figure, these transitions are not shown. Let's get started Initial state 0, input string “HERHEHIS”:
Here they are - all four occurrences. Now let's do the same with the string “HISHER”:
As expected, only three entries were found. Now you can delve into the essence of the examples and formulate the following statement: "Not all occurrences will be found for the input string containing overlapping sample lines in the automaton without suffix references." We are talking about overlapping (“HIS” and “SHE” in “HISHE”), and not part of one another (“HE” and “HER” in “HER”).
In the machine with the suffix links of this, of course, does not occur. Let's check on the same examples. Let us number the states of the automaton with suffix references:
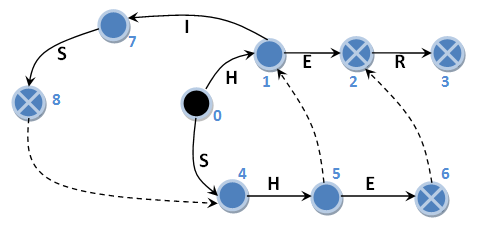
Take the input string “HERHEHIS”:
For a given input line, the progress of the automaton is exactly the same as for an automaton without suffix references. Now let the machine automat the line “HISHER”:
Indeed, all four occurrences were detected. What can be stated here: “Without suffixing references, the hope of finding all occurrences of sample strings tends to zero.”
Often, I met descriptions of the Aho-Korasik algorithm, which ended precisely at this point. The algorithm for constructing the tree was written in detail, but it was written about the search algorithm: “it is elementary - we go over the states and give the result”. And the authors of these works would be absolutely right if they were not mistaken. To begin with, I will show an example that even an automaton with suffix links cannot cope with. We construct a similar automaton, but we introduce into it two additional sample lines: “I” and “IS”. Schematically, such an automaton with its main and suffix transitions can be represented as follows:
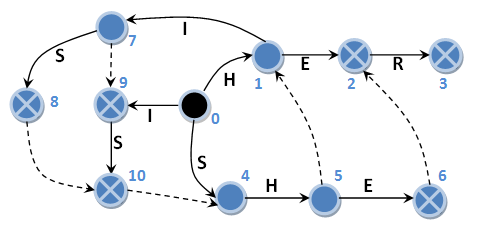
As an input line we take all the same “HISHER” known to us. So, let's go:
Total we have five occurrences found. But among them there is no sample line “I”. What is the matter? How did it happen? In fact, everything is elementary. When passing through the suffix link, we passed state 9, which could be visited only from states 7 and 0. Therefore, everywhere where there is a substring “HIS”, sample line “I” will not be found. Similarly, in the input line “HISHER” we would find the sample string “H” only once, after adding it to the list and building the corresponding automaton. And the point here is not that the strings “I” and “H” consist of one character. Check for yourself: replace “HIS” by “HIPS”, “IS” by “IPS”, “I” by “IP” in the list and feed the input line “HIPSHER” to the machine. The sample IP string will not be found for the same reasons. So what was wrong: the structure of the machine or the search algorithm?
In the solutions to this problem, there is one clear favorite. Faced with a similar example and having understood the reason, the developers choose the most obvious frontal solution: “after switching to the suffix link, run back through the main transitions to the initial state”. Indeed, it saves us from the problem, and such a realization is completely entitled to life. Here you can only note two but:
In the above-mentioned article of user rmq , a different solution is applied: to run not by main transitions, but by suffix links to the initial state, and only by “good suffix links”, that is, by those leading to the state of fixing the sample string. Such an approach is an order of magnitude better than the “fourier” solution, but it still makes it necessary to do extra runs through the states. Despite this, in practical implementation, this algorithm will work over the same time as the original one. Thank you, rmq , for an interesting solution.
Let's return to the original algorithm. For those who are familiar with the original article, or at least with the correct translation of it, they could detect an error even in the very first machine. If for some state to record the fact of detection not only of the complete (from the initial state) of the found sample string, but also all its suffixes, which are also sample strings, then everything will work correctly.
I will cite once again the scheme of the last considered automaton with some modifications.
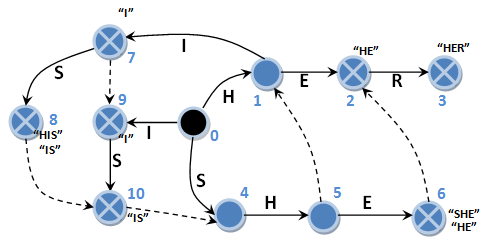
When state 6 is reached, we record occurrences of “SHE” and “HE”. It is on state 6, and not after the transition by the suffix link. Similarly, state 7 will fix the occurrence of sample line “I”, and state 8 will record the occurrence of sample line “HIS” and “IS”. In the search algorithm it is necessary in this case to remove the fixation of the entry after the transition by the suffix link, otherwise the same entry will be recorded twice. For example, after the transition from the 6th state to the 2nd one, it is not necessary to record the occurrence of “HE”, we did it earlier after the transition from the 5th state to the 6th one. Now you do not need any reverse pass to the initial state. The search is really simple and straightforward. Parsing the input string “HISHER” will now look like this:
Great, now all 6 occurrences have been found. It may seem to someone that this complicates the construction of the automaton, but this is not at all the case. It will be no more difficult than our previous example. I did not describe the algorithm for constructing an automaton from the very beginning, therefore I will not give it now. He is beautifully described in the original article by Alfred Aho and Margaret Corasic, which may be worth reading.
In conclusion, I would like to advise those who read something not from the original source to be aware of its possible incorrectness. And if possible, get to the truth before you make another mistake in the implementation. And for those who write “adapted” statements, treat your work more responsibly, without misleading the rest.
Note: the rmq user article , as it turned out, does not contain this error. How it is solved there will tell below. And many thanks to him, if it were not for his topic, I would not have written my own and would not have received an invite!
Before the start, a couple of words about the target audience: Most likely, those who have been familiar with the Aho-Korasik algorithm for a long time will not be interested in my article, since they have long been aware of its features. At least, all my familiar programmers who have repeatedly used this algorithm know about the existence of its incorrect interpretations firsthand. But for beginners and those who did not happen to often use it in practice, this article can be quite useful.
So, let's begin.
In order not to waste the readers' time, I will miss the detailed descriptions of the algorithm (this can be read in the original article) and I will start with an example and a picture in order to quickly run through the terms and talk further "in one language".
Suppose we look for the following list of sample strings: {"HE", "SHE", "HIS", "HER"}. First we need to build an automaton. That finite automaton with states and transitions, on the basis of which the Aho-Korasik algorithm is built. The black circle denotes the initial state of the automaton. Blue circles will denote the next state of the automaton, the achievement of which does not mean the fact of detection of the sample line. And finally, blue circles with a cross-hair are another state of the automaton, the achievement of which means the fact of detection of the sample line. Naturally, transitions stretch between them - black arrows signed by letters, which are a condition for the transition. They will be called the main transitions. In the absence of a main transition for the next input symbol, the automaton switches to the initial state. Let's call them zero transitions. I do not specifically indicate these transitions in order not to clutter up the drawing. For zero transitions, it is worth noting that when you navigate through them, the input symbol is not absorbed, that is, it remains in the input line and will be used again after the transition. The exception is the zero transition from the initial state, where, in fact, the state does not change, and the input symbol is absorbed.

The figure shows four blue circles with a cross, each of which corresponds to one of the rows of patterns. In fact, already in this example the same error was laid. The original algorithm describes the machine a little differently. But first things first.
Recall the so-called suffix links. These are transitions that indicate which state you need to go to if there is no main transition for the next character in the input line. In the following figure, they are indicated by dotted black arrows. We will call them suffixed transitions or suffix links. The transition by suffix links by analogy with the zero transition does not absorb the input character. As in the first case, I do not depict transitions leading to the initial state in the absence of a main transition.

In the example without suffix links, but with zero transitions, all occurrences will be found in the string “HERHEHIS” (“HE”, “HER”, “HE”, “HIS”). But in the input line “HISHER” only three occurrences will be found (“HIS”, “HE”, “HER”) and the machine will not detect the occurrence of the sample string “SHE”, which is easy to verify. In the case of suffix links for the string “HERHEHIS”, the result will be the same, and for the string “HISHER” the result will be a list of four entries found: (“HIS”, “SHE”, “HE”, “HER”). That is, in the latter case, all occurrences were found. No, no, this is not the mistake that I wanted to talk about. In no case do not think so. To someone forgot about the suffix links, I have not seen this before. Still ahead.
I did not begin to describe in detail the algorithm for constructing an automaton, but we will consider the search algorithm for the cases described above in more detail. To do this, for the sake of convenience, we give for the beginning an automaton without suffix links, in which we enumerate its states (blue numbers next to the corresponding circles).

Yes, by the way, let me remind you that, despite the lack of suffix links, this machine goes into the initial state in the absence of the main direction while preserving the input symbol. In the figure, these transitions are not shown. Let's get started Initial state 0, input string “HERHEHIS”:
0 H -> 1 ERHEHIS 1 E -> 2 RHEHIS (“HE”) 2 R -> 3 HEHIS (“HER”) 3 H -> 0 HEHIS // , 0 H -> 1 EHIS 1 E -> 2 HIS (“HE”) 2 H -> 0 HIS // 0 H -> 1 IS 1 I -> 7 S 7 S -> 8 (“HIS”) Here they are - all four occurrences. Now let's do the same with the string “HISHER”:
0 H -> 1 ISHER 1 I -> 7 SHER 7 S -> 8 HER (“HIS”) 8 H -> 0 HER 0 H -> 1 ER 1 E -> 2 R (“HE”) 2 R -> 3 (“HER”) As expected, only three entries were found. Now you can delve into the essence of the examples and formulate the following statement: "Not all occurrences will be found for the input string containing overlapping sample lines in the automaton without suffix references." We are talking about overlapping (“HIS” and “SHE” in “HISHE”), and not part of one another (“HE” and “HER” in “HER”).
In the machine with the suffix links of this, of course, does not occur. Let's check on the same examples. Let us number the states of the automaton with suffix references:

Take the input string “HERHEHIS”:
0 H -> 1 ERHEHIS 1 E -> 2 RHEHIS (“HE”) 2 R -> 3 HEHIS (“HER”) 3 H -> 0 HEHIS // 0 H -> 1 EHIS 1 E -> 2 HIS (“HE”) 2 H -> 0 HIS // 0 H -> 1 IS 1 I -> 7 S 7 S -> 8 (“HIS”) For a given input line, the progress of the automaton is exactly the same as for an automaton without suffix references. Now let the machine automat the line “HISHER”:
0 H -> 1 ISHER 1 I -> 7 SHER 7 S -> 8 HER (“HIS”) 8 H -> 4 HER // 4 H -> 5 ER 5 E -> 6 R (“SHE”) 6 R -> 2 R (“HE”) // 2 R -> 3 (“HER”) Indeed, all four occurrences were detected. What can be stated here: “Without suffixing references, the hope of finding all occurrences of sample strings tends to zero.”
Often, I met descriptions of the Aho-Korasik algorithm, which ended precisely at this point. The algorithm for constructing the tree was written in detail, but it was written about the search algorithm: “it is elementary - we go over the states and give the result”. And the authors of these works would be absolutely right if they were not mistaken. To begin with, I will show an example that even an automaton with suffix links cannot cope with. We construct a similar automaton, but we introduce into it two additional sample lines: “I” and “IS”. Schematically, such an automaton with its main and suffix transitions can be represented as follows:

As an input line we take all the same “HISHER” known to us. So, let's go:
0 H -> 1 ISHER 1 I -> 7 SHER 7 S -> 8 HER (“HIS”) 8 H -> 10 HER (“IS”) 10 H -> 4 HER 4 H -> 5 ER 5 E -> 6 R (“SHE”) 6 R -> 2 R (“HE”) 2 R -> 3 (“HER”) Total we have five occurrences found. But among them there is no sample line “I”. What is the matter? How did it happen? In fact, everything is elementary. When passing through the suffix link, we passed state 9, which could be visited only from states 7 and 0. Therefore, everywhere where there is a substring “HIS”, sample line “I” will not be found. Similarly, in the input line “HISHER” we would find the sample string “H” only once, after adding it to the list and building the corresponding automaton. And the point here is not that the strings “I” and “H” consist of one character. Check for yourself: replace “HIS” by “HIPS”, “IS” by “IPS”, “I” by “IP” in the list and feed the input line “HIPSHER” to the machine. The sample IP string will not be found for the same reasons. So what was wrong: the structure of the machine or the search algorithm?
In the solutions to this problem, there is one clear favorite. Faced with a similar example and having understood the reason, the developers choose the most obvious frontal solution: “after switching to the suffix link, run back through the main transitions to the initial state”. Indeed, it saves us from the problem, and such a realization is completely entitled to life. Here you can only note two but:
- The estimation of the complexity of the algorithm (its time costs) is changing for the worse;
- There was really no problem.
In the above-mentioned article of user rmq , a different solution is applied: to run not by main transitions, but by suffix links to the initial state, and only by “good suffix links”, that is, by those leading to the state of fixing the sample string. Such an approach is an order of magnitude better than the “fourier” solution, but it still makes it necessary to do extra runs through the states. Despite this, in practical implementation, this algorithm will work over the same time as the original one. Thank you, rmq , for an interesting solution.
Let's return to the original algorithm. For those who are familiar with the original article, or at least with the correct translation of it, they could detect an error even in the very first machine. If for some state to record the fact of detection not only of the complete (from the initial state) of the found sample string, but also all its suffixes, which are also sample strings, then everything will work correctly.
I will cite once again the scheme of the last considered automaton with some modifications.

When state 6 is reached, we record occurrences of “SHE” and “HE”. It is on state 6, and not after the transition by the suffix link. Similarly, state 7 will fix the occurrence of sample line “I”, and state 8 will record the occurrence of sample line “HIS” and “IS”. In the search algorithm it is necessary in this case to remove the fixation of the entry after the transition by the suffix link, otherwise the same entry will be recorded twice. For example, after the transition from the 6th state to the 2nd one, it is not necessary to record the occurrence of “HE”, we did it earlier after the transition from the 5th state to the 6th one. Now you do not need any reverse pass to the initial state. The search is really simple and straightforward. Parsing the input string “HISHER” will now look like this:
0 H -> 1 ISHER 1 I -> 7 SHER (“I”) 7 S -> 8 HER (“HIS”, “IS”) 8 H -> 10 HER 10 H -> 4 HER 4 H -> 5 ER 5 E -> 6 R (“SHE”, “HE”) 6 R -> 2 R 2 R -> 3 (“HER”) Great, now all 6 occurrences have been found. It may seem to someone that this complicates the construction of the automaton, but this is not at all the case. It will be no more difficult than our previous example. I did not describe the algorithm for constructing an automaton from the very beginning, therefore I will not give it now. He is beautifully described in the original article by Alfred Aho and Margaret Corasic, which may be worth reading.
In conclusion, I would like to advise those who read something not from the original source to be aware of its possible incorrectness. And if possible, get to the truth before you make another mistake in the implementation. And for those who write “adapted” statements, treat your work more responsibly, without misleading the rest.
')
Source: https://habr.com/ru/post/201952/
All Articles