Five amazing mathematical facts
For a start, a small spoiler

Yes, I know that if you write the name with a capital letter, the incident will not work. Next translation.
Mathematics is one of the few areas of knowledge that can be objectively called true, because its theorems are based on pure logic. But at the same time, these theorems are often very strange and contradictory to intuition.
Some people find math to be boring. The following examples show that she is anything but
')
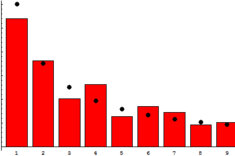
Oddly enough, the random data is actually not that random. In the data presented, representing everything from stock exchange rates to the population of cities, the heights of buildings and the length of rivers, about 30 percent of all numbers begin with one. Smaller numbers start at 2, even less at 3, and so on, with only every twentieth number starting at 9. And the larger the data set, the wider the order of the values covered, the more pronounced this pattern is.

Due to the fact that primes are indivisible (except for one and oneself), and the fact that all other numbers can be represented as their product, primes are often considered as “atoms” in the world of mathematics. Despite its importance, the distribution of primes still remains a mystery. There is no such rule that would unequivocally say which numbers will be simple and how many will meet the next prime number.
The apparent randomness of prime numbers makes the facts found in Ulam 's Table Cloths very strange.
In 1963, the mathematician Stanislav Ulam discovered an amazing pattern when he painted his notebook during the presentation: if you write down integers in a spiral, prime numbers are arranged along diagonal lines. This in itself is not very surprising if one remembers that all prime numbers, except two, are odd, and the diagonal lines in the spirals of integers are alternately odd. More unusual was the tendency of prime numbers to lie mostly on some diagonals and practically absent on others. Moreover, the pattern was observed regardless of the starting date of the spiral (from unity or any other).
Even if the spiral is scaled to accommodate a much larger number of numbers, it can be seen that the accumulation of prime numbers on some diagonals is much denser than on others. There are mathematical assumptions that explain this pattern, but so far they have not been proven.
In one important area of mathematics, called topology, two objects are considered equivalent or homeomorphic if one of them can be transformed into another by twisting or stretching a surface. Objects are considered different if the transformation requires cuts or kinks of the surface.

As an example, consider a torus - a donut-shaped object. If you put it vertically, expand one side and press the top of the same side, you get a cylindrical object with a handle. Among mathematicians, there is a classic joke that topologists cannot distinguish a donut from a cup of coffee.
On the other hand, Mobius tapes - loops with a single bend are not homeomorphic loops without kinks (cylinders), because you cannot straighten the Mobius strip, without cutting it, turning one side and gluing it again.
Topologists have long been interested in the question, will the sphere be homeomorphic to itself when turned inside out? In other words, is it possible to twist the sphere? At first glance, this seems impossible, because it is impossible to pierce a hole in the sphere. But it turns out, turning the sphere is possible. How this is done is shown in the video. .
It is striking that the topologist Bernard Maureen, who is the main developer of the above method of inverting a sphere, is blind.

Despite the fact that the walls can be decorated with an infinite number of curls, in mathematical terms, there are a finite number of individual geometric patterns. All of Escher’s periodical drawings, wallpapers, tile designs, and in general all two-dimensional repeating groups of shapes, can be assigned to one or another so-called “ flat crystallographic group ”. And you know how many such groups exist? Exactly 17.

“As Shakespeare's sonnet captures the very essence of love, or the picture shows the inner beauty of a person, Euler’s equation penetrates into the very depths of existence.”
Stanford mathematician Keith Devlin wrote these words about an equation in an essay in 2002 called The Finest Equation. But why is Euler's formula breathless? And what does it even mean?
First, the letter “e” is an irrational number (with an infinite number of digits), which starts at 2.71828 ... Opened in the context of continuously accrued compound interest, it describes the rates of exponential growth from insect colonies to radioactive decay. In mathematics, the number has a number of unexpected properties, for example, it is equal to the sum of the inverse factorials from zero to infinity. Ultimately, the constant e occupied mathematics, holding out from nowhere, but finding itself in a large number of important equations.
Further. i is the so-called imaginary unit - the square root of minus 1. "So-called", because in reality there is no number that, when multiplied by itself, resulted in a negative number (because negative numbers do not have real square roots) . But in mathematics there are a large number of situations where you have to extract the square root of a negative number. The number i is used as a peculiar note of the place where such an operation was performed.
Pi is the ratio of the circumference to its diameter, one of the favorite and most interesting constants in mathematics. Like e, it appeared in a lot of mathematical and physical formulas as if from nowhere.
The constant e raised to a power imaginary unit multiplied by pi equals minus one. From the Euler equation it follows that the addition to this unit gives zero. It is hard to believe that all these strange numbers, one of which does not even belong to the real world, can be so simply combined. But this is a proven fact.

Yes, I know that if you write the name with a capital letter, the incident will not work. Next translation.
Mathematics is one of the few areas of knowledge that can be objectively called true, because its theorems are based on pure logic. But at the same time, these theorems are often very strange and contradictory to intuition.
Some people find math to be boring. The following examples show that she is anything but
')
5. Random data sets

Oddly enough, the random data is actually not that random. In the data presented, representing everything from stock exchange rates to the population of cities, the heights of buildings and the length of rivers, about 30 percent of all numbers begin with one. Smaller numbers start at 2, even less at 3, and so on, with only every twentieth number starting at 9. And the larger the data set, the wider the order of the values covered, the more pronounced this pattern is.
4. Spirals of prime numbers

Due to the fact that primes are indivisible (except for one and oneself), and the fact that all other numbers can be represented as their product, primes are often considered as “atoms” in the world of mathematics. Despite its importance, the distribution of primes still remains a mystery. There is no such rule that would unequivocally say which numbers will be simple and how many will meet the next prime number.
The apparent randomness of prime numbers makes the facts found in Ulam 's Table Cloths very strange.
In 1963, the mathematician Stanislav Ulam discovered an amazing pattern when he painted his notebook during the presentation: if you write down integers in a spiral, prime numbers are arranged along diagonal lines. This in itself is not very surprising if one remembers that all prime numbers, except two, are odd, and the diagonal lines in the spirals of integers are alternately odd. More unusual was the tendency of prime numbers to lie mostly on some diagonals and practically absent on others. Moreover, the pattern was observed regardless of the starting date of the spiral (from unity or any other).
Even if the spiral is scaled to accommodate a much larger number of numbers, it can be seen that the accumulation of prime numbers on some diagonals is much denser than on others. There are mathematical assumptions that explain this pattern, but so far they have not been proven.
3. Inverting a sphere
In one important area of mathematics, called topology, two objects are considered equivalent or homeomorphic if one of them can be transformed into another by twisting or stretching a surface. Objects are considered different if the transformation requires cuts or kinks of the surface.

As an example, consider a torus - a donut-shaped object. If you put it vertically, expand one side and press the top of the same side, you get a cylindrical object with a handle. Among mathematicians, there is a classic joke that topologists cannot distinguish a donut from a cup of coffee.
On the other hand, Mobius tapes - loops with a single bend are not homeomorphic loops without kinks (cylinders), because you cannot straighten the Mobius strip, without cutting it, turning one side and gluing it again.
Topologists have long been interested in the question, will the sphere be homeomorphic to itself when turned inside out? In other words, is it possible to twist the sphere? At first glance, this seems impossible, because it is impossible to pierce a hole in the sphere. But it turns out, turning the sphere is possible. How this is done is shown in the video. .
It is striking that the topologist Bernard Maureen, who is the main developer of the above method of inverting a sphere, is blind.
2. Mathematics of walls

Despite the fact that the walls can be decorated with an infinite number of curls, in mathematical terms, there are a finite number of individual geometric patterns. All of Escher’s periodical drawings, wallpapers, tile designs, and in general all two-dimensional repeating groups of shapes, can be assigned to one or another so-called “ flat crystallographic group ”. And you know how many such groups exist? Exactly 17.
1. Sonnet

“As Shakespeare's sonnet captures the very essence of love, or the picture shows the inner beauty of a person, Euler’s equation penetrates into the very depths of existence.”
Stanford mathematician Keith Devlin wrote these words about an equation in an essay in 2002 called The Finest Equation. But why is Euler's formula breathless? And what does it even mean?
First, the letter “e” is an irrational number (with an infinite number of digits), which starts at 2.71828 ... Opened in the context of continuously accrued compound interest, it describes the rates of exponential growth from insect colonies to radioactive decay. In mathematics, the number has a number of unexpected properties, for example, it is equal to the sum of the inverse factorials from zero to infinity. Ultimately, the constant e occupied mathematics, holding out from nowhere, but finding itself in a large number of important equations.
Further. i is the so-called imaginary unit - the square root of minus 1. "So-called", because in reality there is no number that, when multiplied by itself, resulted in a negative number (because negative numbers do not have real square roots) . But in mathematics there are a large number of situations where you have to extract the square root of a negative number. The number i is used as a peculiar note of the place where such an operation was performed.
Pi is the ratio of the circumference to its diameter, one of the favorite and most interesting constants in mathematics. Like e, it appeared in a lot of mathematical and physical formulas as if from nowhere.
The constant e raised to a power imaginary unit multiplied by pi equals minus one. From the Euler equation it follows that the addition to this unit gives zero. It is hard to believe that all these strange numbers, one of which does not even belong to the real world, can be so simply combined. But this is a proven fact.
Source: https://habr.com/ru/post/201502/
All Articles