Programming Language J. Why love?

J is the most abnormal and most effective language I know of. It allows you to quickly develop, as well as to cause profanity in people unfamiliar with it and looking at the code.

J is too unusual. And difficult to learn. People facing J lack motivation to learn it. Unusual syntax.
In this post, I wanted to help you look further, what will happen if you study it and how interesting it is. From my own experience I know that the advantages of this language are not immediately obvious. In the post I am not going to stop on the analysis of structures. Only in the review. I suggest just to plunge into the examples, try to feel the power of the language. Find out what is beautiful language, without learning. Writing articles that teach programming in it is difficult and I think it is not necessary. It is not so simple to do this briefly, and there are no problems with the training materials on the official website. The main desire. And we will do it.

A bit of history

Until J was APL . The APL language was developed by Kenneth Iverson while teaching computational mathematics at Harvard in the 1950s. Especially for teaching, he developed his notation. Then this language was transferred to the machines and became known as APL (modest: A Program Language). APL works with arrays and is optimized for working with them.
')
The APL language has a slight flaw. Operations are indicated by non-standard characters. To work with him need a special keyboard. Thus, there is a need to create a new language, more friendly to standard input devices. Iverson initiated the creation of an APL dialect that uses ASCII characters. So Kenneth Iverson together with Roger Hue in the early 90s created the language J. At this time, Arthur Whitney “broke away” from the Iverson team. He had a disagreement about how to create J, and started creating his own language, K. Which also became a successful language.

Overview J

Download and install J can be on the link www.jsoftware.com . There are also educational materials and various documentation.

J is a functional language. But the language is not ordinary, not classical functional. Not lispodobny. The data unit is an n-dimensional array, not a list.

J is an interpreter (in this implementation). With dynamic typing.

Expressions are constructed from verbs, nouns, adverbs, gerundi, alliances and other things. We are in this post will be interested in verbs (analogue of a function / operation) and nouns (data). Nouns are not exactly given, as in imperative languages. They are mountable. Thus, what is called assignment in J is rather a “naming”.

The noun is an n-dimensional array. You can create a noun, for example, like this:

3 5 $ 0

We get a two-dimensional array of 3 by 5, consisting of zeros. You can get an array of any dimension. A special case is an array of zero dimensionality - this is a scalar. One-dimensional array - vector. Thus, the unit of data in J is an n-dimensional array. To build an array filled with not numbers, but the numbers we need, after the $ sign we can write the necessary data separated by a space. For example, the string:

3 5 $ 1 2 3

Create and output an array of 3 by 5 and fill in turn with a repeating sequence 1 2 3:

1 2 3 1 2
3 1 2 3 1
2 3 1 2 3

To create a scalar, one number is enough:

a =: 4

Here I have already shown how the name is assigned. Those. a we already have 4 . To create a vector, it’s enough to write numbers in a string separated by a space:

4 5 3 6
4 5 3 6

* As you may have guessed, J is working interactively and immediately displays the result.

Now about the types. In J, besides the dimensionality of the array, there is a type of its elements. Those. elements are always of the same type. There are several numeric types: logical (0, 1), whole, whole with any number of characters, rational, real, complex. Also, along with the numeric types there are special numbers: minus infinity, infinity, uncertainty. Dynamic typing J is great for mathematical operations - on each operation it will determine which numbers are in it. For example, if we apply the square root to the matrix of integers, we can get either real or complex numbers. Depending on the elements of the original array.

Also in J, besides numeric types there is
1) character (literal). J can also process text. The text in case J is a vector of characters. To set a character, you need to enclose it in single quotes. To set a vector of characters - just enclose the text in single quotes.
2) boxing (boxed, boxed) is a packaged type. Those. Any matrix can be packed and get boxed. And from the boxes you can make an array. With the help of boxes, thus, you can create trees.
And a few more special types, which are not considered.

With the nouns sorted out. Now, what are the verbs.
A verb is similar to an operation in mathematical expression in other languages. There are two kinds of verbs in J: monadic (monad) and dyadic (dyad). This is similar to unary and binary operations. And it gives a great opportunity: to create verbs we do not need names for input data. Input data is always one or two - right and left.

There are special rules for how to form a single verb from other verbs, without using any variable names.

So, the first standard example:

avg =: + / % #

The verb avg is the arithmetic mean of the vector. Pay attention to his body - only 4 characters. Here we have only three verbs - add the numbers ( + / ), take the length of the vector ( # ) and divide the first by the second ( % ).

* Fold the numbers in the vector denoted by the symbols + and /. The first is the sum of two numbers, and the second is to put the operation between all the elements (i.e., left fold). Since the slash is occupied, the division operation in J is denoted by%.

Create a vector and apply our verb to it:

a =: 5 3 7 0 2 4
avg a
3.5

Got the arithmetic mean of the vector.

How does this magic happen? J uses such simple rules. First, operations in J have no priority and are performed from right to left . If we write an expression:

2 * 3 + 4
14

We get 14, not 10. Which, in general, simplifies the construction of expressions. If you need to change the order - brackets are used:

( 2 * 3 ) + 4
ten

Do not worry, these were just expressions that calculate values ​​directly, and when we wrote avg =: + / % # , then we asked the verb by combining verbs.

Now let's look at how the arithmetic mean verb works.
When a verb consists of three verbs in a row, then first verbs are applied to nouns, and then the middle verb is applied to the right and left verb in relation to it.
Like this:


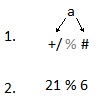
If the verb consists of 5 verbs, then first three right verses are executed, as shown above, then two are taken to the left and in the same order it is executed further. For example, the verb of taking the maximum of two elements: ">.". Therefore, the maximum from the list: "> ./"
And we write a verb that finds the sum of the maximum value and the arithmetic average:

d =: >. / ++ / % #

Apply to vector:

da
10.5

How it works:

Notice that when I write “how it works,” I don’t mean that I know the order in which these verbs are performed. I only explain the meaning of how to understand such a line of verbs. With a string of verbs we say what we want. And how - J. decides

I have described above only one of the rules for constructing expressions. Just so that you grasp the essence, as it is possible, briefly describe complex algorithms in a line and what is the secret of laconicism J. Naturally, J is not enough sense to describe everything in the post.

Sometimes it is impossible to describe a task in such a way that the verbs accept only two simple arrays as arguments (left and right). Sometimes you need to write verbs, analogs of functions with a large number of arguments. This can be bypassed by boxing. Those. You can set the vector of boxes in which, in fact, lie a number of different values, similar to the input parameters of a function in other languages. And in the verb you can get them out and unpack. Also in the verbs implemented recursion.

The above form of recording verbs in J is called tacit.

Now a few examples, without explaining how they work.

Examples

1. INNER JOIN

Consider this example in SQL. We have two tables:

CREATE TABLE Customers (ID INT, Name TEXT, Age INT, Salary INT) CREATE TABLE Orders (OID INT, Date DATETIME, CustomerID INT, Amount INT) 

Somehow we fill them. And such a request:

 SELECT * FROM Orders o INNER JOIN Customers c ON o.CustomerID = c.ID AND o.Amount < 2000 

Specially I connect tables not by equality, but through a more complex predicate, in order to complicate the task a little.
And try to do the same on J.

createTable =: [: |:,. & a:
union =: ( [: {. [ ) ,: [: ( [: <[:;] # ~ ~: & a:) " 1 ( [: {: [ ) ,. ( [: {:] ) { ~ ( [: {.] ) i. [: {. [
insert =: [ union [: ( {.,: ( [: ( [: <[: ( ] $ ~ [: 1 & , # ) > ) " 0 {:) ) [: |: [:>]
rows =: {. ( [: <,:) " 1 1 [: |: [: ( [: < " 1 [:,.> ) " 0 {:
value =: [: ( ] ` {. @. ( [: 1 & = # )) [:, [:> [ ((( [: <[ ) = [: {.] ) # [: {:] ) [:>]
pr =: [:, [: (( [:> [ ) (( [: < ( [:> [ ) ,. [:>] ) " 0 0 ) " 0 1 [:>] ) / [: ( [ : <[: rows > ) " 0 ]
join =: 1 : '((([: {. [:> {.),: ​​[: ([: <(> " 0)) " 1 [: {: [: 1 2 0 & |: [:> ( [:, u " 0) #]) (pr y)) '

In general, this is all the code that allows you to solve this problem. The necessary verbs are. Create and fill tables:

Customers =: createTable 'ID' ; ' Name ' ;' Age ' ;' Salary '
Orders =: createTable 'OID' ; ' Date ' ;' CustomerID ' ;' Amount '

Customers =: Customers insert ( <' ID' ; 1 ) , ( <' Name' ; ' Ramesh' ) , ( <' Age' ; 32 ) , ( <' Salary' ; 2000 )
Customers =: Customers insert ( <' ID' ; 2 ) , ( <' Name' ; ' Khilan' ) , ( <' Age' ; 25 ) , ( <' Salary' ; 1500 )
Customers =: Customers insert ( <' ID' ; 3 ) , ( <' Name' ; ' kaushik' ) , ( <' Age' ; 23 ) , ( <' Salary' ; 2000 )
Customers =: Customers insert ( <' ID' ; 4 ) , ( <' Name' ; ' Chaitali' ) , ( <' Age' ; 25 ) , ( <' Salary' ; 6500 )
Customers =: Customers insert ( <' ID' ; 5 ) , ( <' Name' ; ' Hardik' ) , ( <' Age' ; 27 ) , ( <' Salary' ; 8500 )
Customers =: Customers insert ( <' ID' ; 6 ) , ( <' Name' ; ' Komal' ) , ( <' Age' ; 22 ) , ( <' Salary' ; 4500 )
Customers =: Customers insert ( <' ID' ; 7 ) , ( <' Name' ; ' Muffy' ) , ( <' Age' ; 24 ) , ( <' Salary' ; 10000 )

Orders =: Orders insert ( <' OID' ; 102 ) , ( <' Date' ; ' 2009 - 10 - 08' ) , ( <' CustomerID' ; 3 ) , ( <' Amount' ; 3000 )
Orders =: Orders insert ( <' OID' ; 100 ) , ( <' Date' ; ' 2009 - 10 - 08' ) , ( <' CustomerID' ; 3 ) , ( <' Amount' ; 1500 )
Orders =: Orders insert ( <' OID' ; 101 ) , ( <' Date' ; ' 2009 - 11 - 20' ) , ( <' CustomerID' ; 2 ) , ( <' Amount' ; 1560 )
Orders =: Orders insert ( <' OID' ; 103 ) , ( <' Date' ; ' 2008 - 05 - 20' ) , ( <' CustomerID' ; 4 ) , ( <' Amount' ; 2060 )


Check that we have in the tables:

Customers

ID	Name	Age	Salary
one 2 3 four five 6 7	Ramesh Khilan kaushik Chaitali Hardik Komal Muffy	32 25 23 25 27 22 24	2000 1500 2000 6500 8500 4500 10,000

Orders

OID	Date	CustomerID	Amount
102 100 101 103	2009-10-08 2009-10-08 2009-11-20 2008-05-20	3 3 2 four	3000 1500 1560 2060

And the query with the predicate:

(( [: 2000 & > 'Amount' & value ) *. 'CustomerID' & value = 'ID' & value ) join Customers ; < Orders

ID	Name	Age	Salary	OID	Date	CustomerID	Amount
2 3	Khilan kaushik	25 23	1500 2000	101 100	2009-11-20 2009-10-08	2 3	1560 1500

That's how simple it is. Note that J is a generic language and does not have the means to handle relational data. The code that is above, before creating and populating tables, is all logic. join can accept any predicate.

The example is not really difficult, because arrays are somewhat similar to tables, and boxes (boxes) J draws in rectangles, which allows you to immediately display the tables.

2. Sudoku Solver

i =:, (( , |:) i. 9 9 ) ,,. / , / i. 4 $ 3
c =: ( # = [: # ~. ) @ -. & 0
t =: [: (( [: * / _9: c \ ] ) " 1 #] ) i & {+ " 1 1 ( >: i. 9 ) * / [: i & = i. & 0
r =: [:, ` $: @. ( 0: e., ) [:; ( < @ t ) " 1
s =: 9 9 & $ @ r @ ,


This is all code. Create an input matrix:
] m =: 9 9 $ ". " 0 '200370009009200007001004002050000800008000900006000040900100500800007600400089001'
2 0 0 3 7 0 0 0 9
0 0 9 2 0 0 0 0 7
0 0 1 0 0 4 0 0 2
0 5 0 0 0 0 8 0 0
0 0 8 0 0 0 9 0 0
0 0 6 0 0 0 0 4 0
9 0 0 1 0 0 5 0 0
8 0 0 0 0 7 6 0 0
4 0 0 0 8 9 0 0 1

We apply the verb to it and get the solution:
sm
2 8 4 3 7 5 1 6 9
6 3 9 2 1 8 4 5 7
5 7 1 9 6 4 3 8 2
1 5 2 4 9 6 8 7 3
3 4 8 7 5 2 9 1 6
7 9 6 8 3 1 2 4 5
9 6 7 1 4 3 5 2 8
8 1 3 5 2 7 6 9 4
4 2 5 6 8 9 7 3 1

3. Prolog

I want to show the code in J for a more practical task and not close to matrices / arrays. I heard doubts that the vector approach is suitable for parsing. The idea came to choose a simple task for the post, the solution of which is associated with parsing. I implement Prolog. More precisely, not all Prolog, because The task is not practical and I don’t want to spend a lot of time and effort. This will be a Prolog subset to show that, in principle, a tacit form of recording is suitable for such tasks. In this Prolog-e, if you can call it that, there will not even be a cut-off. Only simple facts and rules, the operation "and", "or". So, the code:

frq =: [: -. [: ( 2: | + / ) \ '' '' & =
sp =: ( # @ [ ) ( [: <[}. [:>] ) " 0 0 [ ( ] < /. ~ [: + / \ E. *. [: frq ] ) ,
spf =: [: <[: ( [: ',' & sp [: -. & ')' = & '(' { " 0 1 ,. & ',' ) >
cl =: # ~ [: -. e. & ( 33 {. A. ) *. frq
parse =: [: ( [: <[: (( spf @ {. ) , ( }. ` ( [: <[: ( [: <[: spf " 0 [: '),' & sp > ) " 0 [: ');' & sp [:> {:) @. ( 2: = # ))) [: ': -' & sp > ) " 0 _1:}. [: '.' & sp cl

isVar =: [: ( 91 & > *. 64 & < ) [: a. & i. [: {.>
replace =: (( ) i. ~ [: (. [ ) { ( [: {: [ ) ,] ` ( [: <[$: [:>] ) @. ( [: 32 & = [: 3 ! : 0 [:>] )) " 2 0
gp =: [:> [: {.>
gv =: [: ( # ~ [: +. / " 1 isVar " 0 ) ,.
suit =: ( [ ( 0: ` (( [: ( # = [: # [: ~. [: {. |:) [: ~. [: ( # # [: -. [: isVar " 0 [: {: |:) gv ) *. ( [: *. / [: +. / [: ( isVar " 0 , = / ) ,:) ) @. (( [: # [ ) = [: #] )) [: gp ] ) " 1 0 #]
sr =: [ ( ] ( replace ~ [: |:] ) " 2 [: (( [: -. [: isVar {:) " 1 #] ) [ gv ~ [: gp ] ) " 1 0 suit
groupVars =: [: ( [: <] $ ~ 2 :, ~ [: -: # ) " 1 [:> [: ( [: <[:; ( > @ [ ) ( [: <, " 1 1 ) " 1 2 ( > @ ] )) / ] < / . ~ [: {. |:
isRuleTrue =: ( [: +. / ( [: *. / ] ( isTrue ~ [:>] ) " 1 0 [:> [ ) " 0 1 ) ` ( 0: <[: # getVarsFromRule ) @. ( 0: <# @ gv @ ; @ ; @ [[ )
isTrue =: ] (( a: & e. @ ] ) +. [: +. / [ ( isRuleTrue ~ [:>] ) " 1 0 [: -. & a: ] ) [: {: [: |: [: -. & ( a:, a:) [: ( 0 2 $ a:) & , [:> sr
getVars = :; (( [: <[: ~. ( > @ {. @ [ ) gv [: gp ] ) ` (( > @ {. @ [ ) $: ( < @ < @ gp @ ] ) ( [ replace ~ [: |: [:>] ) " 0 0 ( }. @ [ ) GetVarsFromRule ~ [:> [: {: [:>] @. ( [: <: [:: [:>] )) " 1 0 sr
getVarsFromRule =: ] (( [: {.] ) # ~ [ ( isRuleTrue ~ [:>] ) " 1 0 [: {:] ) [: |: [ ( ], [: <[ replace ~ [: |: [:>] ) " 1 0 [:] ` groupVars @. ( 0: <# ) [: ~. [:; [:;] ( [: <[ getVars ~ [:>] ) " 1 0 [:; [

goal =: ( [: < S: 0 [: {. [: parse [:, & '.' ] ) ( [: { & ( > 'No' ; 'Yes' ) isTrue ) ` ( [: ( ] ` (( > @ {. ) , [: '=' & , [:> {:) @. ( 2: = # )) " 1 [:> getVars ) @. ( [: +. / [: IsVar " 0 [ ) ( [: parse [ )

This is all code. Actually, the parser in the first part of the solution. The task of parsing such a simple Prolog is, of course, primitive. But still, J can be used for parsing. And for more complex parsing tasks.
The only "complexity" in the parser - Prolog allows the creation of atoms from arbitrary characters, if they are taken in single quotes. Otherwise the parser would be much shorter. And yet, I specifically do not use any library verbs. In order for you to appreciate the power of the language itself, how quickly you can write something from scratch. There is also a library for working with text. There is a library for working with regular expressions.

Let's set the code for Prolog:
prolog_code =: 0 : 0
male (jeff).
male (fred).
female (mary).
parents (jeff, vince, jane).
parents (mary, vince, jane).

sister_of (x, y): - female (x),
parents (X, F, M),
parents (Y, F, M).
)

And a couple of questions.
“Does Mary have to be sister to Fred?”:
prolog_code goal 'sister_of (mary, fred)'
No
“Who is Mary's sister?”:
prolog_code goal 'sister_of (mary, X)'
X = jeff

X = mary

Conclusion

I hope you understand how J can briefly solve complex problems. At the expense of ease, you may have doubts.

The purpose of the examples is to show the code in tacit form. Did you notice that there are practically no non-standard library verbs in the code? All code is almost punctuation. These are elementary verbs of J. Of course, no one forces you to write like this, without introducing your own verbs, without giving them meaningful names. But the high level J predisposes by virtue of the brevity of the code not to introduce new names. The price of efforts to create a new code is small, which leads to the fact that less often you want to hide the code behind the name. In general, over time, this leads to the fact that a J programmer reads the same verbs, of which there are not many, and as time goes on, it becomes better and better to read the code. The code becomes clearer and clearer.

I think that every programmer who works in some mainstream OOP language will sadly agree what the hell is with libraries and frameworks. Correct programming practices call for encapsulating code, hiding behind meaningful names. If the effort to create the code is large enough, more names appear. And when, for example, you come to a new team to work with a project, there is little left of the language in the code - you need to learn new entities for you, everything that the previous programmers gave the names. Learning a new language is always threatening to study libraries, and their number is growing rapidly. J does not solve this problem, but postpones.

J as a language has a fairly high threshold of entry. At first, he practically does not read. Having studied all the verbs, you can hardly write on it, but you cannot even read your code. But over time, you can do it easier and easier. This will not happen with other languages.

Also, it should be mentioned that this does not mean that J has weak support and there are not enough libraries in it. There are a lot of developments already, from working with excel-files, databases, to working with video. Also J is multi-paradigm, it can be written not only in tacit form, but also in imperative. With cycles and branches. With error handling. J supports OOP.

Working with J does not resemble encoding, but output the formula. You, at first, will peer into the code, the speed of dialing is much lower. But with all of this, the result will be even faster at first than in other languages. Even without having very great experience and readability of the code, in time it turns out that sitting down to solve the problem in J seems much easier than solving it in any other, more familiar language. Working with J is like working with a powerful calculator, not a programming language. You do not have the feeling that you create something for centuries. The speed of getting a result gives you more courage in coding and you can easily try various options.

Because of this, J has a niche - data processing, especially in the financial sphere. On J it is easy to “rotate” the data, test various hypotheses. And if you need to - save the script and use as a program. J is convenient in projects for data processing. Where complex algorithms are needed. Moreover, by the complexity of the algorithms, I mean “useful complexity”, i.e. complexity of data conversion, not algorithms for optimization. With all this, J is sufficiently productive. Do not be afraid that he is an interpreter. The interpreter is only in the sense that it executes expressions line by line. But if the verb expression is written in the string, then it performs it once, remembering, and then when applying the verb to the data, it works quickly. Since usually processed data of large volume, the optimization in J show good performance. J can also work with libraries written in other languages. That allows you to optimize problem areas.

This language, due to its properties, is good for prototyping. In this case, the prototype has a great chance not to be rewritten, because or performance will be satisfied, or you can optimize only problem areas.

This is all well and good, but there is one problem in using J in team projects — few specialists. If you decide to use J in a project, there is a high probability that you will not find people.

And, nevertheless, J can be used not only for team work. It gives a strong learning effect. Working with J changes his views on algorithms in general, "turns the mind." It has a positive impact on working with other languages.

Also this language is very convenient for work, as an auxiliary language. My environment J is always open and I do not use a calculator or excel. When you need to parse something or generate code for another language - J is a great tool.

Links

1. Official website: www.jsoftware.com
2. I propose to read a great article - Programming Language J, Introduction