Spaces with a different number Pi
Recently, on Habré, in one article, they mentioned the question “What would happen to the world if Pi was 4?” I decided to reflect a little on this topic, using some (even if not the most extensive) knowledge in relevant areas of mathematics. Who cares - I ask under the cat.
To imagine such a world, you need to mathematically realize a space with a different ratio of the circumference of a circle to its diameter. This is what I tried to do.
')
Say at once that I will consider only two-dimensional spaces. Why? Because the circle itself is defined in a two-dimensional space (if we consider the dimension n> 2, then the ratio of the measure of the (n-1) -dimensional circle to its radius will not even be a constant).
So for starters, I tried to come up with at least some space where Pi is not equal to 3.1415 ... For this, I took a metric space with a metric in which the distance between two points is equal to the maximum among the modules of the coordinate difference (ie , Chebyshev distance ).
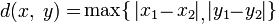
What kind will the unit circle have in this space? Take a point with coordinates (0,0) for the center of this circle. Then the set of points, the distance (in the sense of a given metric) from which to the center is 1, is 4 segments parallel to the axes of the coordinates, forming a square with side 2 and with center at zero.
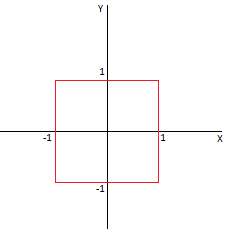
Yes, in some metric this is a circle!
Calculate here Pi. The radius is 1, then the diameter, respectively, is 2. You can also consider the definition of the diameter as the greatest distance between two points, but even so it is 2. It remains to find the length of our “circle” in this metric. This is the sum of the lengths of all four segments, which in this metric have a length max (0,2) = 2. Hence, the circumference is 4 * 2 = 8. Well, then Pi is equal to 8/2 = 4. Happened! But do you really need to rejoice? This result is practically useless, because the space in question is absolutely abstract, it does not even define corners and turns. Can you imagine a world where, in fact, there is no turn, and where the circle is a square? I tried, honestly, but I didn’t have enough imagination.
Realizing that I got a result, though interesting, but absolutely useless (in the sense of understanding the structure of the world with a different number Pi), I decided to try to build a space model with certain concepts of angles and turns (that is, a space with a given non-degenerate scalar product). Of course, I wanted the metric to remain a metric in the classical sense of the word (that is, the distance between two points was real and non-negative). But then the scalar product must be positively defined, whence it follows that the space must be Euclidean . Or at least locally Euclidean, that is, variety . You can not bother with all these concepts, but just read on :)
I admit, I killed some time trying to come up with a clever Euclidean metric with bad number Pi. I considered the lengths of the resulting “circles”, recalling various integral formulas, until the obvious fact reached me: if the space is Euclidean, then by replacing the coordinates you can get our usual space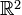
in which the number pi is known. Hence, in another Euclidean space, it will not change its value. Sadness
Since we still want corners and turns, but we are not satisfied with Euclidean space, we will try to consider pseudo - Euclidean type (1,1) (since we are only interested in two-dimensional ones). It differs from the usual Euclidean space in that the square of the distance between two points (and, as a result, the scalar product of two vectors) can be negative. In order not to suffer too much, I took the metric in which the scalar product in Cartesian coordinates will look like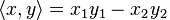
. What kind of circle will take a single radius? This will be a set of points given by the equation 
, that is ... Hyperbole.
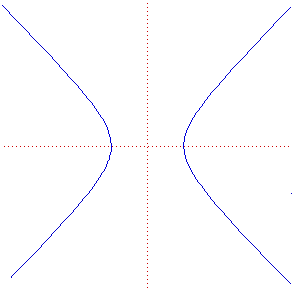
Yes Yes! In a certain space, and this is a circle.
The radius is 1, but there are some difficulties with finding the length of this “circle”. After some searching for information on the Internet, I came to the conclusion that in a pseudo-Euclidean space such a thing as “Pi number” cannot be determined at all, which is certainly bad.
If someone in the comments tells me how to formally calculate the length of a curve in pseudo-Euclidean space, I will be very happy, because my knowledge of differential geometry, topology (as well as hard googling) was not enough for this.
I do not know whether it is possible to write about the conclusions after such not very long research, but something can be said. First, trying to imagine a space with a different number Pi, I realized that it would be too abstract to be a model of the real world. Secondly, when trying to come up with a more successful model (similar to ours, the real world), it turns out that Pi will remain unchanged. If we take for granted the possibility of a negative square of the distance (which is simply absurd for an ordinary person), then Pi will not be determined at all! All this suggests that perhaps there could not be peace with another Pi? It’s not for nothing that the Universe is exactly what it is. Or maybe this is real, just ordinary mathematics, physics, and human imagination are not enough for this. What do you think?
Upd. I found out for sure. The length of a curve in pseudo-Euclidean space can be defined only on some of its Euclidean subspaces. That is, in particular, for the “circle” obtained in the N3 attempt, such a concept as “length” is not defined at all. Accordingly, it is also impossible to count Pi there.
To imagine such a world, you need to mathematically realize a space with a different ratio of the circumference of a circle to its diameter. This is what I tried to do.
')
Attempt # 1.
Say at once that I will consider only two-dimensional spaces. Why? Because the circle itself is defined in a two-dimensional space (if we consider the dimension n> 2, then the ratio of the measure of the (n-1) -dimensional circle to its radius will not even be a constant).
So for starters, I tried to come up with at least some space where Pi is not equal to 3.1415 ... For this, I took a metric space with a metric in which the distance between two points is equal to the maximum among the modules of the coordinate difference (ie , Chebyshev distance ).
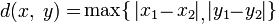
What kind will the unit circle have in this space? Take a point with coordinates (0,0) for the center of this circle. Then the set of points, the distance (in the sense of a given metric) from which to the center is 1, is 4 segments parallel to the axes of the coordinates, forming a square with side 2 and with center at zero.
Yes, in some metric this is a circle!
Calculate here Pi. The radius is 1, then the diameter, respectively, is 2. You can also consider the definition of the diameter as the greatest distance between two points, but even so it is 2. It remains to find the length of our “circle” in this metric. This is the sum of the lengths of all four segments, which in this metric have a length max (0,2) = 2. Hence, the circumference is 4 * 2 = 8. Well, then Pi is equal to 8/2 = 4. Happened! But do you really need to rejoice? This result is practically useless, because the space in question is absolutely abstract, it does not even define corners and turns. Can you imagine a world where, in fact, there is no turn, and where the circle is a square? I tried, honestly, but I didn’t have enough imagination.
Attempt # 2.
Realizing that I got a result, though interesting, but absolutely useless (in the sense of understanding the structure of the world with a different number Pi), I decided to try to build a space model with certain concepts of angles and turns (that is, a space with a given non-degenerate scalar product). Of course, I wanted the metric to remain a metric in the classical sense of the word (that is, the distance between two points was real and non-negative). But then the scalar product must be positively defined, whence it follows that the space must be Euclidean . Or at least locally Euclidean, that is, variety . You can not bother with all these concepts, but just read on :)
I admit, I killed some time trying to come up with a clever Euclidean metric with bad number Pi. I considered the lengths of the resulting “circles”, recalling various integral formulas, until the obvious fact reached me: if the space is Euclidean, then by replacing the coordinates you can get our usual space
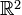in which the number pi is known. Hence, in another Euclidean space, it will not change its value. SadnessAttempt number 3.
Since we still want corners and turns, but we are not satisfied with Euclidean space, we will try to consider pseudo - Euclidean type (1,1) (since we are only interested in two-dimensional ones). It differs from the usual Euclidean space in that the square of the distance between two points (and, as a result, the scalar product of two vectors) can be negative. In order not to suffer too much, I took the metric in which the scalar product in Cartesian coordinates will look like
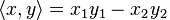. What kind of circle will take a single radius? This will be a set of points given by the equation , that is ... Hyperbole.Yes Yes! In a certain space, and this is a circle.
The radius is 1, but there are some difficulties with finding the length of this “circle”. After some searching for information on the Internet, I came to the conclusion that in a pseudo-Euclidean space such a thing as “Pi number” cannot be determined at all, which is certainly bad.
If someone in the comments tells me how to formally calculate the length of a curve in pseudo-Euclidean space, I will be very happy, because my knowledge of differential geometry, topology (as well as hard googling) was not enough for this.
Findings:
I do not know whether it is possible to write about the conclusions after such not very long research, but something can be said. First, trying to imagine a space with a different number Pi, I realized that it would be too abstract to be a model of the real world. Secondly, when trying to come up with a more successful model (similar to ours, the real world), it turns out that Pi will remain unchanged. If we take for granted the possibility of a negative square of the distance (which is simply absurd for an ordinary person), then Pi will not be determined at all! All this suggests that perhaps there could not be peace with another Pi? It’s not for nothing that the Universe is exactly what it is. Or maybe this is real, just ordinary mathematics, physics, and human imagination are not enough for this. What do you think?
Upd. I found out for sure. The length of a curve in pseudo-Euclidean space can be defined only on some of its Euclidean subspaces. That is, in particular, for the “circle” obtained in the N3 attempt, such a concept as “length” is not defined at all. Accordingly, it is also impossible to count Pi there.
Source: https://habr.com/ru/post/201452/
All Articles